本小节目标:将 Transformers 的能力引入图神经网络
1 从 Transformers 到 GNN
前置知识:Transformer 基础、第三方资料-图解 Transformer
多头自注意力机制:
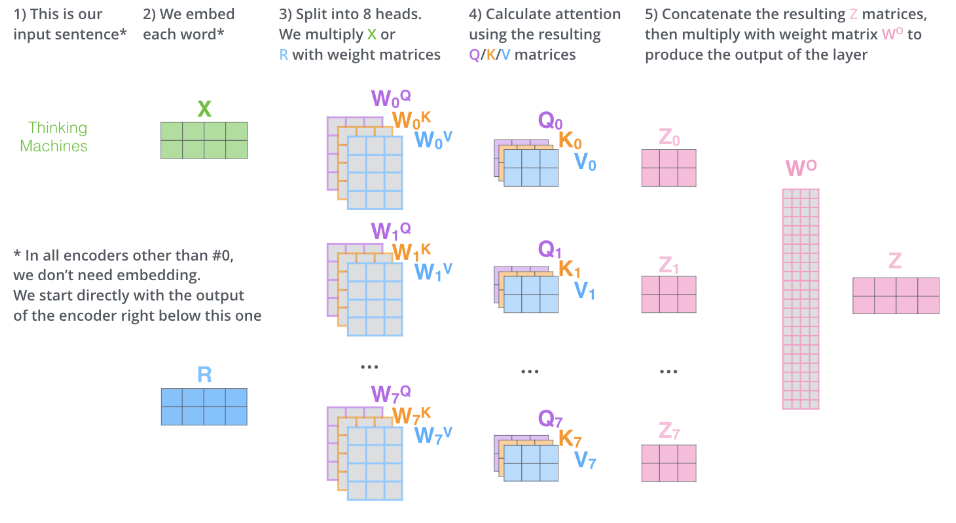
对比 Transformer 和 RNN:
- 相似点:输入一系列向量(无特定顺序),并输出一系列嵌入
- 不同点:GNN 使用消息传递,Transformer 使用自注意力机制
对比消息传递和自注意力机制:
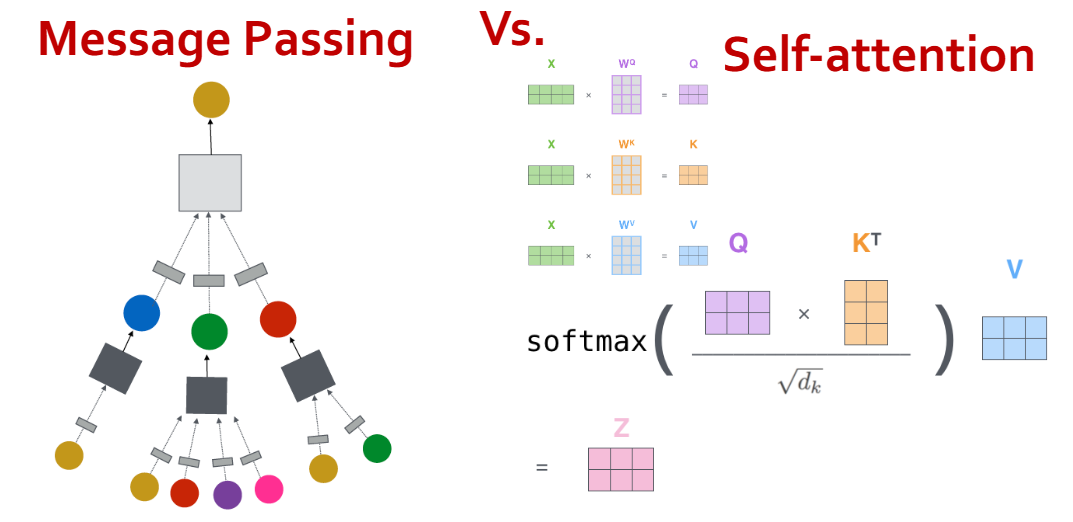
- 自注意力是消息传递的一个特例,是一种在全连接图上的消息传递
- 给定一个图 $G$,将节点 $i$ 的自注意力 softmax 约束在邻居节点 $j$ 上(即 GAT)
2 GAT 的设计空间
GNN 的设计空间 VS GAT 的设计空间:
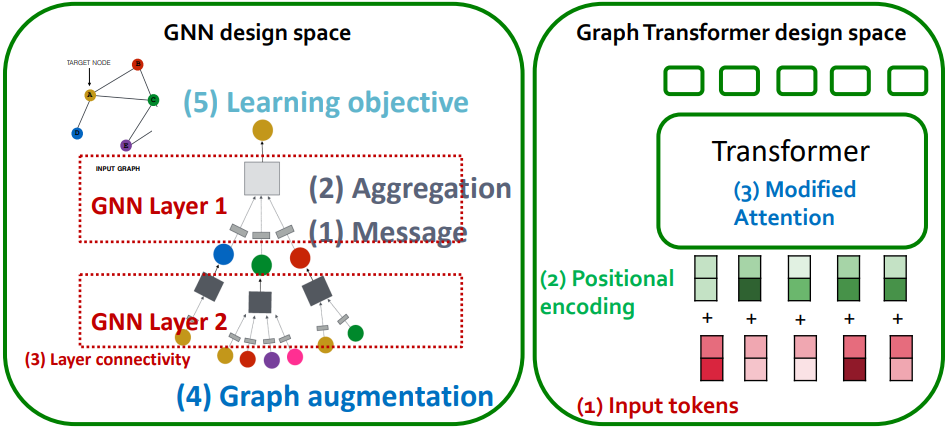
- GAT 的输入内容需要包含节点特征、邻接信息和边特征,分别对应上图中的(1)Input tokens,即节点的嵌入表示(2) Positional encoding,节点的位置编码(包含节点的邻接信息)(3)Modified Attention,改进的自注意力机制 (纳入边特征信息)
由于 Transformer 模块对输入 token 的顺序不敏感,因此往往都需要额外的位置编码
常见的位置编码方法:
- 基于相对距离的位置编码:即节点与其他节点的相对距离组成的向量
- 基于拉普拉斯特征向量的位置编码:特征向量继承了图论基础#3.1 理解拉普拉斯矩阵捕获的图结构信息
补充实验:基于拉普拉斯矩阵特征向量预测图是否有环的任务
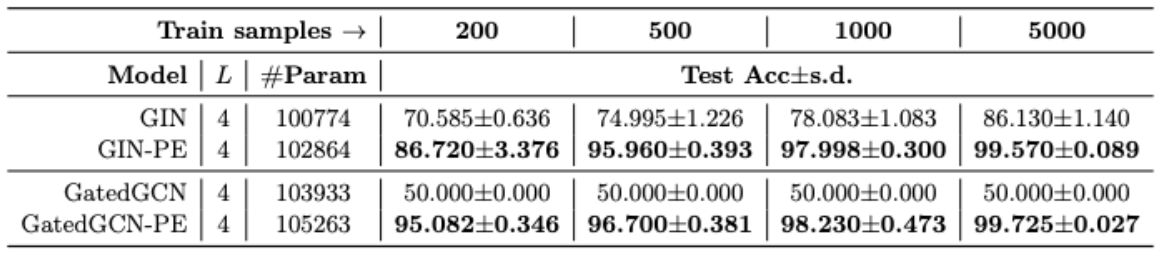
- 上图中 PE 即表示输入包含拉普拉斯矩阵特征向量
- 上图结果表明,拉普拉斯矩阵特征向量捕获了图结构
较小特征值对应的拉普拉斯矩阵特征向量包含着图的局部结构
较大特征值对应的拉普拉斯矩阵特征向量包含着图的全局结构
改进的自注意力机制 :
- 原始的自注意力计算:$Att(X)=softmax(K^TQ)T$
- 定义 $[k_{ij}] = K^TQ$ 作为注意力得分矩阵,其中 $k_{i,j}$ 描述了 token $j$ 对 token $i$ 更新的贡献度
- 因此引入额外的注意力得分 $c_{ij}$,用于描述边特征信息对 token $i$ 更新的贡献度
- 当节点 $i$ 与节点 $j$ 之间存在边特征 $e_{ij}$ 时,定义注意力得分 $c_{ij}=w_1^Te_{ij}$;当节点 $i$ 与节点 $j$ 之间不存在边时,找到两节点间的最短边路径 $(e^1,e^2,...,e^n)$,定义注意力得分 $c_{ij}=\Sigma_n w_n^Te_{n}$
- 其中 $w_1,w_2,...,w_n$ 均为可学习的参数
3 拉普拉斯位置编码的改进
拉普拉斯位置编码的局限性:
- 定义拉普拉斯矩阵 $L$,其对应的特征向量为 $v:=Lv=\lambda v$
- 由以上定义可知,拉普拉斯特征向量存在以下特性:$L(-v)=\lambda (-v)$
- 由此可知,拉普拉斯特征向量的符号是任意的(正的、负的都可以)
- 但是对于神经网络来说,向量的符号对输出的影响是巨大的
解决思路 1:让神经网络兼容拉普拉斯特征向量的符号随机性
- 借助数据增强的技巧,即在神经网络的训练过程中随机翻转特征向量的符号
- 该方法是具备可行性,但对神经网络的训练要求较高(需要翻转的符号太多)
解决思路 2:额外训练一个神经网络,消化特征向量的符号随机性
- 设计一个神经网络 SignNet,实现 $f(v)=f(-v)$
SignNet 的基本结构如下: $$\begin{aligned}&f (v_1, v_2,...,v_k)=\rho (\phi (v_1),+\phi (-v_1),...,\phi (v_k),+\phi (-v_k))\end{aligned} $$
- 其中 $\rho$ 和 $\phi$ 可以是任意神经网络,比如 MLP 或 GNN 等
- 当存在 $\rho$ 和 $\phi$ 满足上式时,神经网络 $f$ 则具备符号不变性
SignNet 的结构可以表达任意的符号不变函数
SignNet 的实践:
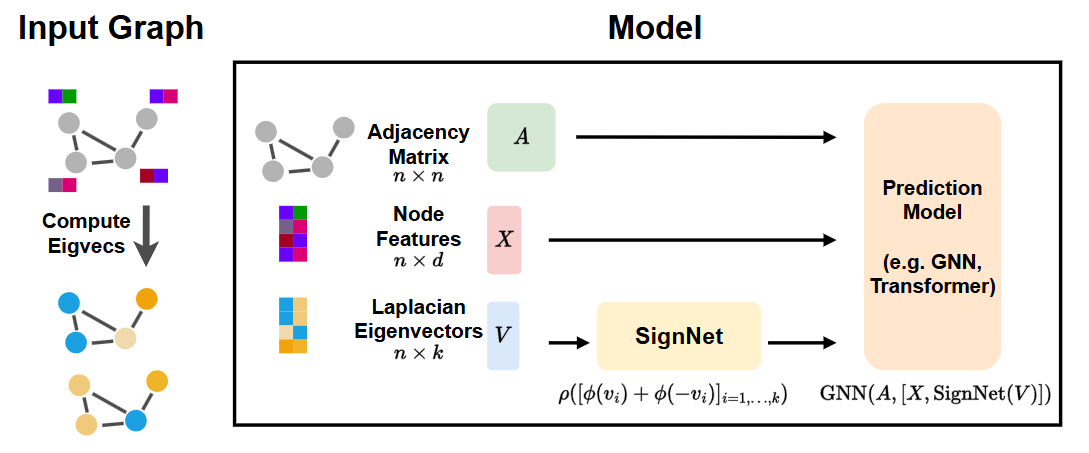
- 对于给定的图输入,先计算邻接矩阵、节点特征、拉普拉斯特征向量
- 拉普拉斯特征向量通过 SignNet 映射为符号不变的特征向量嵌入表示
- 最后借助反向传播梯度联合训练SignNet 和主模型 Prediction Model
在一项预测化学分子的溶解度任务中,SignNet 的添加降低了 50% 的测试误差