BM25（Best Matching 25），一种经典的信息检索方法
- BM25 综合考虑了 TF-IDF 和文档长度等信息，计算效率高，实用性强
- BM25 在信息检索领域使用广泛，是 Elasticsearch 的默认检索方法
- BM25 的语义理解能力不足，无法有效捕捉词序信息和上下文关系
- BM25 可以通过调整参数来适用不同的应用场景，但个性化能力有限
TF-IDF
词频 TF（Term Frequency），词语 $t$ 在文档 $d$ 中出现的频率
$$ \text{TF}(t, d) = \frac{\text{词t在文档d中的出现次数}}{\text{文档d的总词数}} $$
逆文档频率 IDF（Inverse Document Frequency），词语 $t$ 在所有文档 $D$ 中的罕见程度
$$ \text{IDF}(t, D) = \log\left(\frac{\text{文档集合D的总文档数}}{\text{包含词t的文档数} + 1}\right) $$
“罕见程度”描述了一种信息量，一个文档中的“罕见词”往往包含着文档的更多信息
词语 $t$ 的 TF-IDF 值是二者的乘积，能衡量一个词语对于某个文档的重要程度 $$ \text{TF-IDF}(t, d, D) = \text{TF}(t, d) \times \text{IDF}(t, D) $$
- TF-IDF 值简单易用，容易理解，同时考虑了词频和文档信息
- TF-IDF 值忽略了词序和语义，并可能过分强调了高频词的影响
BM25 算法
给定查询 $Q={q_1,..,q_i,...,q_n}$ 和文档 $d$ ，BM25 的计算公式如下： $$ \text{BM25}(Q,d) =\sum_{i=1}^{n}\mathrm{IDF}(q_{i})\cdot\frac{TF(q_{i},d)\cdot(k_{1}+1)}{TF(q_{i},d)+k_{1}\cdot\left(1-b+b\cdot\frac{|d|}{\mathrm{avgdl}}\right)}$$
- $TF(q_{i},D)$ 和 $\mathrm{IDF}(q_{i},D)$ 分别表示第 $i$ 个查询词 $q_i$ 的 TF 值和 IDF 值
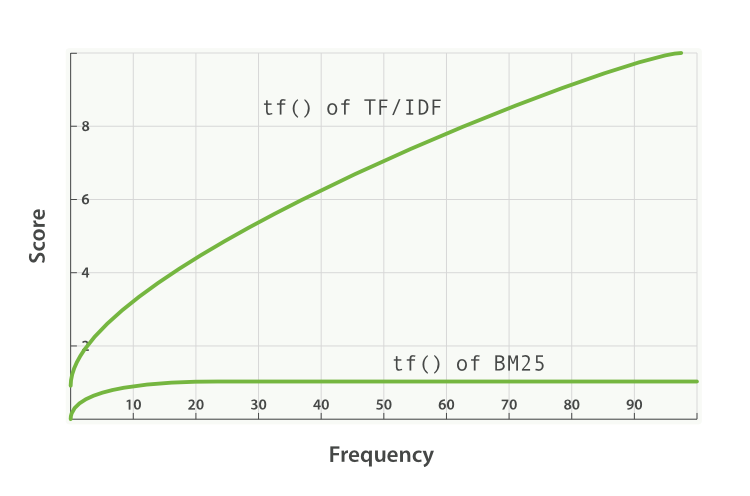
- 在上式分母的右下角部分中，$|d|$ 表示当前文档长度，$avgdl$ 表示文档平均长度；二者的组合 $\frac{|d|}{\mathrm{avgdl}}$ 表示文档长度的归一化项；当前文档长度较大时，BM25 值减少，最终导致文档的得分下降
- 剩余变量中， $k_1$ 和 $b$ 都是可调整的超参数，其中 $k_1$ 的默认值为 1.2，$k_1$ 的增加会增大词频对搜索排序的作用；$b$ 的默认值为 0.75，$b$ 的增加会增大文档长度对搜索排序的作用
需要注意的是，BM25 对 $\mathrm{IDF}$ 的计算方式进行了细节调整： $$ \text{IDF}(q_i) = \ln\left( 1+\frac{N-n(q_i)+0.5}{n(q_i)+0.5} \right) $$
- 其中 $N$ 表示文档总数，$n(q_i)$ 表示包含查询词 $q_i$ 的文档总数
BM25 进阶
常见的 BM25 算法变种：
- BM11：对应当 $b=1$ 时的 BM25 算法
- BM15：对应当 $b=0$ 时的 BM25 算法
- BM25F：针对不同文本（标题/正文/引用）分别计算 BM25 后加权
- BM25+：添加额外的超参数，用于补偿对于长文档的低评分问题
词频对 BM25 和 TF-IDFD 的影响（图源）
