课程目标 1:GNN 与传统图算法的关系
课程目标 2:理解 GNN 学习映射的过程
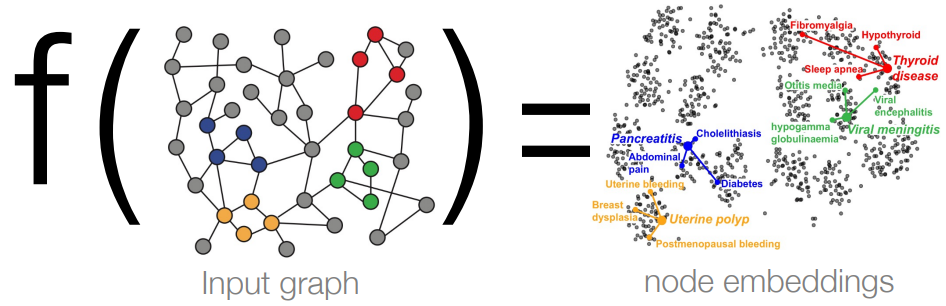
1 GNN 与经典任务
前置知识:WL 图同构检验、4 图同构网络 GIN
前置知识的概括总结:
- GIN 是 1-WL 算法的“神经版本”,二者的表现力相似
- 只不过 GIN 用可学习的 MLP 替换了 1-WL 的 HASH 函数
- 未经训练的 GNN(随机 MLP = 随机哈希)接近 1-WL 算法
思考:除了 1-WL,GNN 还可以轻松地模拟哪些其他任务?
任务 1:特征提取
- 输入:一堆包含颜色、位置描述的物体
- 输出:给定一个物体,说明它的颜色或位置
- 分析:不需要先验知识,很适合 MLP 网络
MLP 很容易学习平滑函数(例如,线性、对数、指数) MLP 不擅长学习复杂函数(例如,平滑函数的总和、for 循环)
任务 2:汇总统计
- 输入:一堆包含颜色、位置描述的物体
- 输出:x 坐标最大的物体的颜色
- 分析:单层 MLP 网络不太适合,需要大量数据来学习(模拟循环的过程);多层 MLP 网络(DeepSets)适合,是对 softmax 函数的拟合
任务 3:关系型 argmax
- 输入:一堆包含颜色、位置描述的物体
- 输出:距离最远的两个物体的颜色
- 分析:任务需要比较成对的物体,多层 MLP 不适合建模;但 GNN 适合建模成对关系,GNN 的节点更新依赖于其他节点
2 GNN 适合的任务
任务 4:最短路径问题
- 输入:加权图和选定的初始节点
- 输出:规划能遍历所有节点的最短路径
- 分析:动态规划与 GNN 的形式非常相似(都是 for 循环的嵌套),因此 GNN 适合解决这类问题
最短路径问题的常见思路,是通过递归的方式将问题分解为相同问题类型的较小实例,然后再依次进行解决
任务 4 实验分析:
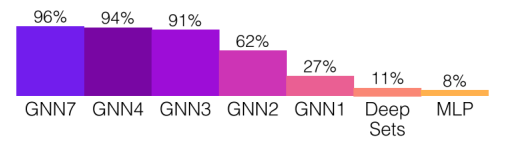
- 7 层的 GNN 取得了最佳的性能
总结:GNN 消息传递是一种动态规划算法,对于可以通过动态规划解决的任务,GNN 会是一个不错的架构选择
3 算法对齐及其应用
算法对齐(Algorithmic Alignment):设计神经网络架构的一般原则
给定目标算法 $g$,将其分解一系列简单函数的组合: $g=g_m \odot...\odot g_1$,则其对应的神经网络架构为 $$f=f_m \odot...\odot f_1$$
- 其中每个 $f_i$ 都包含少量的可学习参数,因此可以轻松学习 $g_i$
关键:将整体算法拆分成单独的简单步骤,可以更容易神经网络的学习
应用 1:给定一组数字 $S$,判断是否存在和为 $k$ 的子集

- 该任务是一个 NP-hard 问题,无法通过动态规划解决,因此不适合 GNN
- 穷举搜索:遍历循环 $S$ 的所有子集,并检查子集的和是否为 $k$
- 穷举搜索转变为神经网络架构:$NES=MLP(max_{\tau \in S}LSTM(X_1,...,X_{|\tau|}|))$;其中 $LSTM$ 用于检查子集的和,$max$ 聚合函数用于寻找最佳子集,$MLP$ 用于映射真值(给出最终判断)
应用 1 实验分析(NES 模型的效果最佳):
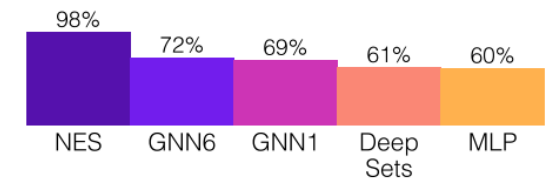
线性算法对齐假设:可以证明外推法对于线性目标函数是完美的,这也意味着神经网络可以推断出看不见的数据,即可在不可预见的未来情况下稳定运行