图表示学习
发表评论
360 views

图表示学习方法一般包括图嵌入表示和图神经网络

  • 图嵌入表示（Node Embedding）为每个节点学习一个嵌入表示（低维稠密向量），使得在原始网络中相似的节点，它们的嵌入表示也更为相似
  • 图神经网络（Graph Neural Networks）通过聚合邻域节点的信息来生成节点的表示

图嵌入表示

基于随机游走的图嵌入经典方法：

  • 等长度、无偏的随机游走：DeepWalk (2014 KDD Perozzi et al.)
  • 有偏的、局部与全局视角权衡的随机游走：node2vec (2016 KDD Grover and Leskovec)
  • 同时优化一阶、二阶邻近度：LINE (2015 WWW Tang et al.)

图嵌入方法的缺陷

  • 无法利用节点、边和图特征/结构信息，仅使用了网络邻接矩阵作为输入
  • 无参数共享，每个节点学习的嵌入表示向量就是要训练的参数
  • 直推式学习（transductive learning）：无法为训练中没有见到的节点生成嵌入表示

DeepWalk

DeepWalk 使用随机游走策略对节点进行采样，利用游走过程中节点间的共现关系来学习节点的向量表示；作为图嵌入表示的经典算法，常作为 baseline 活跃在不同论文中~

DeepWalk 的思路和 1_study/DeepLearning/基础神经网络/word2vec 系列（skip-gram） 类似，在 DeepWalk 中“两个节点出现中同一次随机游走中”，可类比为 word 2 vec 中“两个单次出现在同一处上下文中”；因此二者的优化策略本质是一致

换言之，也可以把一篇文章的每段话看作"在字/词网络中的一次随机游走"

DeepWalk 的核心技巧：

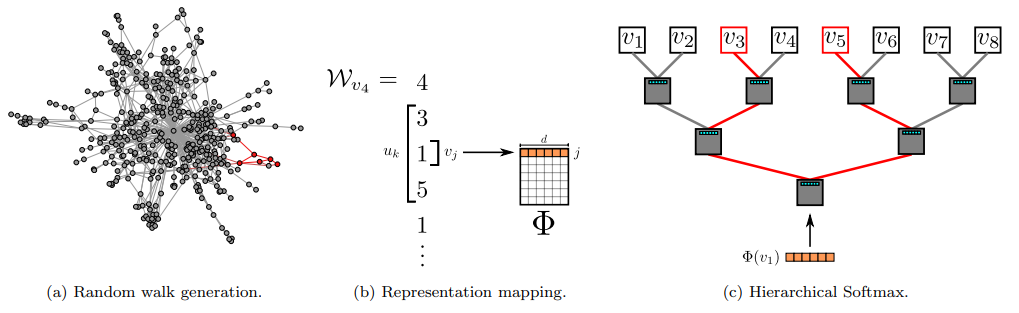
  • （a）数据：首先以每个顶点为起点，随机游走 $\gamma$ 次，每次游走的最大长度为 $t$
  • （b）训练：把每次随机游走的节点序列看作"上下文"，借助 skip-gram 算法训练神经网络 $\Phi$，训练目标是最大化每次游走序列内节点的共现概率；最终得到每个节点的嵌入表示低维向量
  • （c）优化：为了加快训练时间，可以使用 Hierarchical Softmax 来近似概率分布；将随机游走的起点分配给二叉树的叶子，此时预测问题就会变成最大化树中特定路径的概率；此外还可以借助霍夫曼编码，减少树中频发元素的访问时间（给频繁访问的顶点分配较短的路径）

node2vec

node2vec 的核心思想：在 DeepWalk 的基础上进行随机游走策略的改进——使用灵活的、有偏差的随机游走，实现在网络的局部视图（BFS）和全局视图（DFS）之间的权衡

具体来说，node2vec 引入两个超参数 $p$ 和 $q$ 来控制随机游走的策略；假设随机游走当前处于节点 $t$，则游走测录有 $\alpha$ 的概率达到节点 $x$，即： $$ \left.\alpha_{pq}(t,x)= \left\{\begin{array}{ll}\frac1p&\quad\text{if}d_{tx}=0 \\1&\quad\text{if}d_{tx}=1 \\\frac1q&\quad\text{if}d_{tx}=2\end{array}\right.\right. $$

  • 其中 $d_{tx}$ 表示节点 $t$ 与节点 $x$ 间的最短路径长度
  • 为方便理解，公式对应的图示如下：

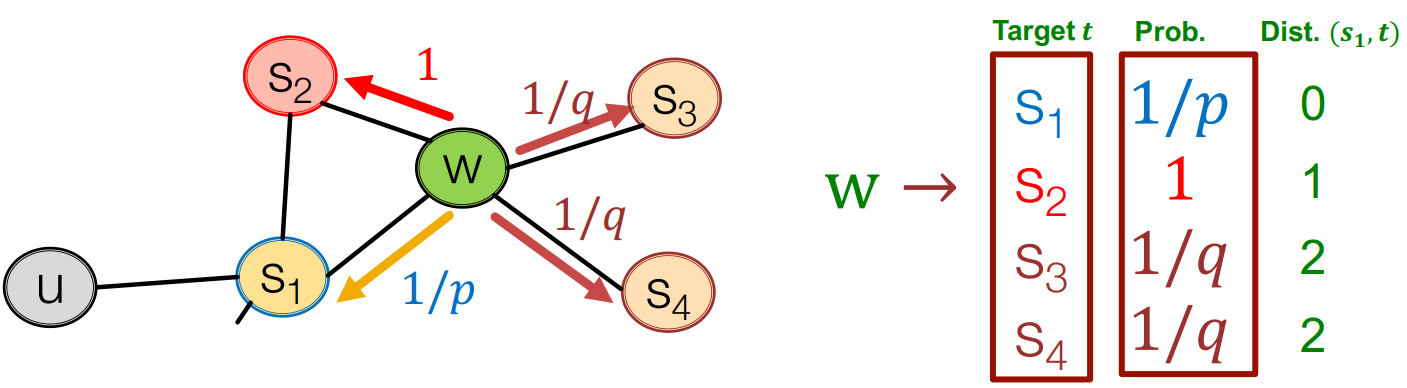
超参数 $p$ 和 $q$ 对探索策略（BFS/DFS）的影响：

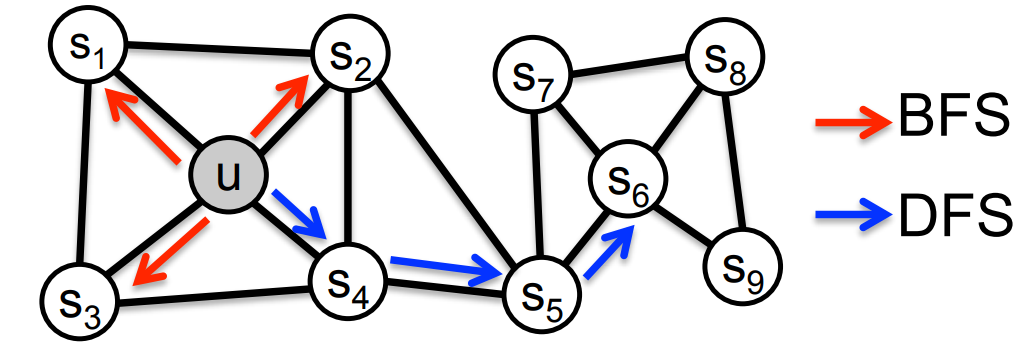
  • 深度优先（DFS），即 q 值小，此时策略更鼓励探索；节点表示更重视同质（homophily）等价
  • 广度优先（BFS），即 p 值小，此时策略的探索更保守；节点表示更重视结构（structural）等价
  • 当 p=q=1 时，策略不再具有明显的探索偏好性；此时，node2vec 退化为 DeeoWalk

除了随机游走策略，node2vec 与 DeppWalk 在损失函数和训练等方面无显著差异

LINE

LINE 不再采用随机游走的方法，而是直接基于一阶/二阶邻近度进行优化

更多算法细节可参阅原始论文：LINE：针对大规模信息网络的嵌入表示

struc2vec

struc2vec 通过遍历多层图（而不是原始网络）的加权随机游走来生成节点的上下文序列，并通过序列的相似性度量来评估并编码节点的结构相似性，增强了对图的结构信息捕捉

更多算法细节可参阅原始论文：struc2vec：从结构性标识中学习节点的表示

图神经网络

推荐直接阅读：CS224W 图机器学习04：GNN 深入理解

该节课程笔记涵盖了 GCN、GraphSAGE 和 GAT 三种经典的 RNN 层

图同构网络 GIN

通过构建单射的邻域聚合函数来增强模型的表达能力

更多细节可参阅： 图同构网络 GIN

Cluster-GCN

Cluster-GCN 算法——解决大规模图的内存消耗问题

  • 图聚类（Metis 或 Graclus）将图预先划分为可小批量操作的子图
  • 限制卷积操作仅在特定子图内进行，从而忽略了邻域爆炸的问题
  • 随机保留不同分区间的链接，避免有偏估计影响最终模型的性能

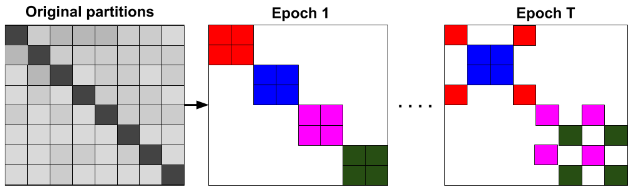
  • 颜色代表每批次维护的邻接信息，每个时期可能不同

更多细节可参阅原始论文：Cluster-GCN

往年同期文章