中文标题:struc2vec: 从结构性标识中学习节点的表示
英文标题:struc2vec: Learning Node Representations from Structural Identity
发布平台:ACM SIGMOD
发布日期:2017-08-04
引用量(非实时):1288
DOI:10.1145/3097983.3098061
作者:Leonardo F.R. Ribeiro, Pedro H.P. Saverese, Daniel R. Figueiredo
关键字: #struc2vec #图嵌入
文章类型:conferencePaper
品读时间:2024-03-22 16:16
1 文章萃取
1.1 核心观点
struc2vec,一种新颖且灵活的框架,用于学习节点结构身份的潜在表示。struc2vec 通过遍历多层图(而不是原始网络)的加权随机游走来生成节点的上下文序列,并通过序列的相似性度量来评估并编码节点的结构相似性。struc2vec 对节点的编码仅依赖于节点上下文结构的相似性,而不考虑节点和边的属性和“距离”
数值实验表明,DeepWalk 等算法适用于节点分类等任务,而本问题提出 struc2vec 能够捕获更强的结构同一性概念,更贴近真实网络的场景(比如具有相同政治倾向的两个博客,相似度应该更强),实现了更优越的性能
1.2 综合评价
- 在捕捉结构同质性方面能力较强,算法经典,简单有效
- 算法鲁棒性和可拓展性强,具备处理大规模网络的能力
- 可以考虑除 DTW 外的距离度量方法或更多的分层方法
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
2.1 算法细节
struct2vec 的算法步骤:
- 确定不同邻域大小情况下,每个顶点对的结构相似性(考虑层次结构信息)
- 根据邻域大小构建一个多层加权图,每一层都包含网络中的所有节点
- 每个节点在多层加权图中进行加权随机游走,生成上下文序列
- 应用 Skip-Gram 等技术根据上下文序列学习节点的潜在表示(略)
2.1.1 定义结构相似度
核心思想:
- 度相同的两个节点在结构上相似;如果它们邻居的度也相同,那它们在结构上更相似
- 目的:在不使用任何节点或边属性的情况下确定两个节点之间的结构相似性
- 注意:相似性度量需要分层以应对不同的邻域大小,捕获更精细的结构相似性概念
定义节点 $u$ 和节点 $v$ 对应 $k$ 跳邻域下的结构距离如下: $$ f_{k}(u,v)=f_{k-1}(u,v)+g(s(R_{k}(u)),s(R_{k}(v))) $$
- 其中 $R_k(u)$ 是距离节点 $u$ 在 $k$ 跳范围内的节点集合
- $s(S)$ 表示对节点集合 $S$ 进行按度排序的序列
- $g(D_1,D_2)$ 测量了按度排序后的两个序列间的距离
- 限制条件: $f_{-1}=0$,$k\ge0$,$|R_{k}(u)|>0$, $|R_{k}(v)|>0$
在本文中,主要使用 时间序列距离测度 DTW 来测量两个序列间的距离。DTW 可以用来衡量两个不同长度且含有重复元素的的序列的距离,其中任意两个元素间的距离定义如下: $$ d(a,b)=\frac{max(a,b)}{min(a,b)}-1 $$
当 $a=b$ 时,$d(a,b)=0$;由此可知当 $D_1=D_2$ 时,$g(D_1,D_2)=0$
$d(1,2)$ 远大于 $d(101,102)$,该距离函数的特性更符合预期
为方便理解,展示按度排序的两个序列的生成过程:
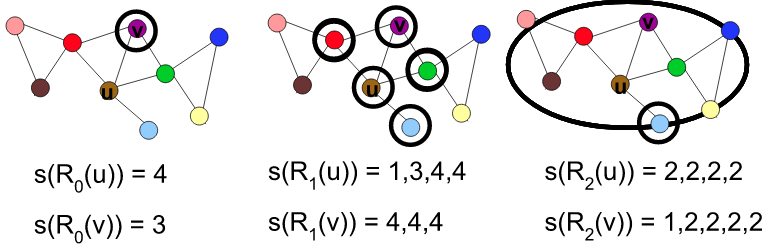
2.1.2 构建多层加权图
多层加权图中每一层图都包含网络中的所有节点
第 $k$ 层加权图中节点 $u$ 和节点 $v$ 之间的边权重定义如下: $$ w_{k}(u,v)=e^{-f_{k}(u,v)},\quad k=0,...,k^{*} $$
- 其中 $f_k(u,v)$ 表示两个节点的 $k$ 跳邻域下的结构距离
- $k^{*}$ 表示本文定义的最大邻域直径(即 $k$ 的理论最大值)
- 边权值 $w_k$ 与结构距离 $f_k$ 成反比,并且值小于等于 1
- 当且仅当结构距离 $f_k=0$ 时,边权值为 1
第 $k$ 层加权图中节点 $u_k$ 与上下层的节点 $u_{k-1},u_{k+1}$ 相连,对应的边权值定义如下: $$ \begin{array}{l}w(u_k,u_{k+1})=\log(\Gamma_k(u)+e),k=0,...,k^*-1 \\w(u_k,u_{k-1})=1,k=1,...,k^*\end{array} $$
- $\Gamma_k(u)$ 表示第 $k$ 层中与节点 $u$ 相连并且边权重大于第 $k$ 层平均边权重的边数量
- $\Gamma_k(u)=\sum_{v\in V}\mathbb{1}(w_k(u,v)>\overline{w}_k)$,其中 $\overline{w}_k$ 表示第 $k$ 层的平均边权重
2.1.3 生成节点的上下文
struct2vec 基于有偏随机游走在多层加权图中生成节点的上下文(游走过的节点序列)
有偏随机游走策略:
- 对于每个节点,随机游走策略从第 $0$ 层开始,每次游走的长度固定且较短
- 每次游走时考虑层切换,在当前层游走的概率为 $q$ ,换层游走的概率为 $1-q$
- 在第 $k$ 层从节点 $u$ 游走到节点 $v$ 的概率为 $p_k(u,v)$:($Z_k(u)$ 为标准化因子)
$$ p_k(u,v)=\frac{e^{-f_k(u,v)}}{Z_k(u)}=\frac{e^{-f_k(u,v)}}{\sum\limits_{{v\in V,v\neq u}}e^{-f_k(u,\upsilon)}} $$
有偏随机游走策略会优先选择在结构上与当前顶点更相似的节点
- 决定换层时,策略使用以下公式来计算游走到上一层/下一层的概率:
$$ \begin{aligned}p_k(u_k,u_{k+1})&=\frac{w(u_k,u_{k+1})}{w(u_k,u_{k+1})+w(u_k,u_{k-1})} \\p_k(u_k,u_{k-1})&=1-p_k(u_k,u_{k+1})\end{aligned} $$
当节点 $u$ 在第 $k$ 层与很多节点都相似时(此时 $\Gamma_k(u)$ 值更大,因此 $w(u_k,u_{k+1})$ 更大),说明节点所处的层过低(在当前层所能考虑到的信息太少),所以节点更容易游走到更高层;反之亦然
- 最终得到每个节点的多次独立游走记录(即节点的多个上下文)
2.1.4 算法的效率优化
优化 1:压缩按度排序的序列
- 对于序列中的每个度数,我们计算该度数出现的次数
- 由于网络中的许多节点往往具有相同的度,因此压缩序列会小很多
- 调整 DTW 中的距离函数计算($a_0$ 表示度,$a_1$ 表示度出现的次数):
$$ \operatorname{dist}(\boldsymbol{a},\boldsymbol{b})=\left(\frac{\max(a_0,b_0)}{\min(a_0,b_0)}-1\right)\max(a_1,b_1) $$
上式最终得到原始序列对于 DTW 的近似值(牺牲一定的精度)
优化 2:减少不必要的相似度计算
- 两个度差异很大的节点,对应的结构距离很大,因此采样概率很低
- 通过二分法查询并保留与节点 $u$ 相似的节点,将边的计算量从 $n^2$ 压缩到 $nlogn$
优化 3:限制多层加权图的层数
- 当 $k$ 较大时,对应的 $k$ 跳节点过少,并且 $f_k$ 和 $f_{k-1}$ 也会很相似
- 不考虑 $k$ 远大于顶点间平均距离的情况,减少不必要的计算和存储开销
2.2 实验分析
节点潜在表示间的距离分布分析:
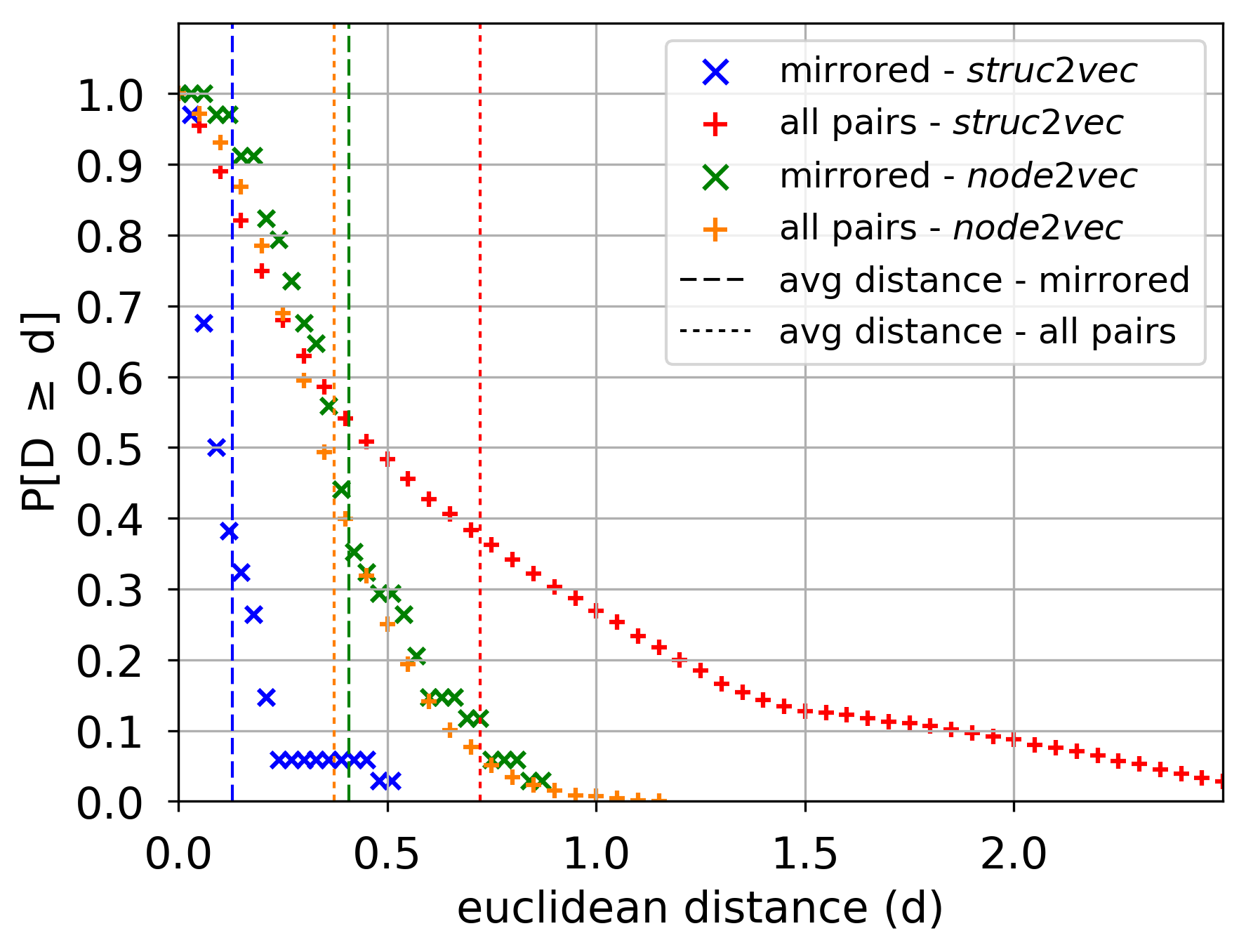
- 蓝色/红色标记分别表示 struct2vec 中镜像节点/所有节点之间的距离分布
- 绿色/橙色标记分别表示 node2vec 中镜像节点/所有节点之间的距离分布
- 相比于 node2vec,struct2vec 更能区分出镜像节点(蓝色与红色的差异明显)
- struct2vec 对不相似的节点具备更明显的区分度(红色曲线拖尾现象明显)
空中交通网络中的分类能力评估:
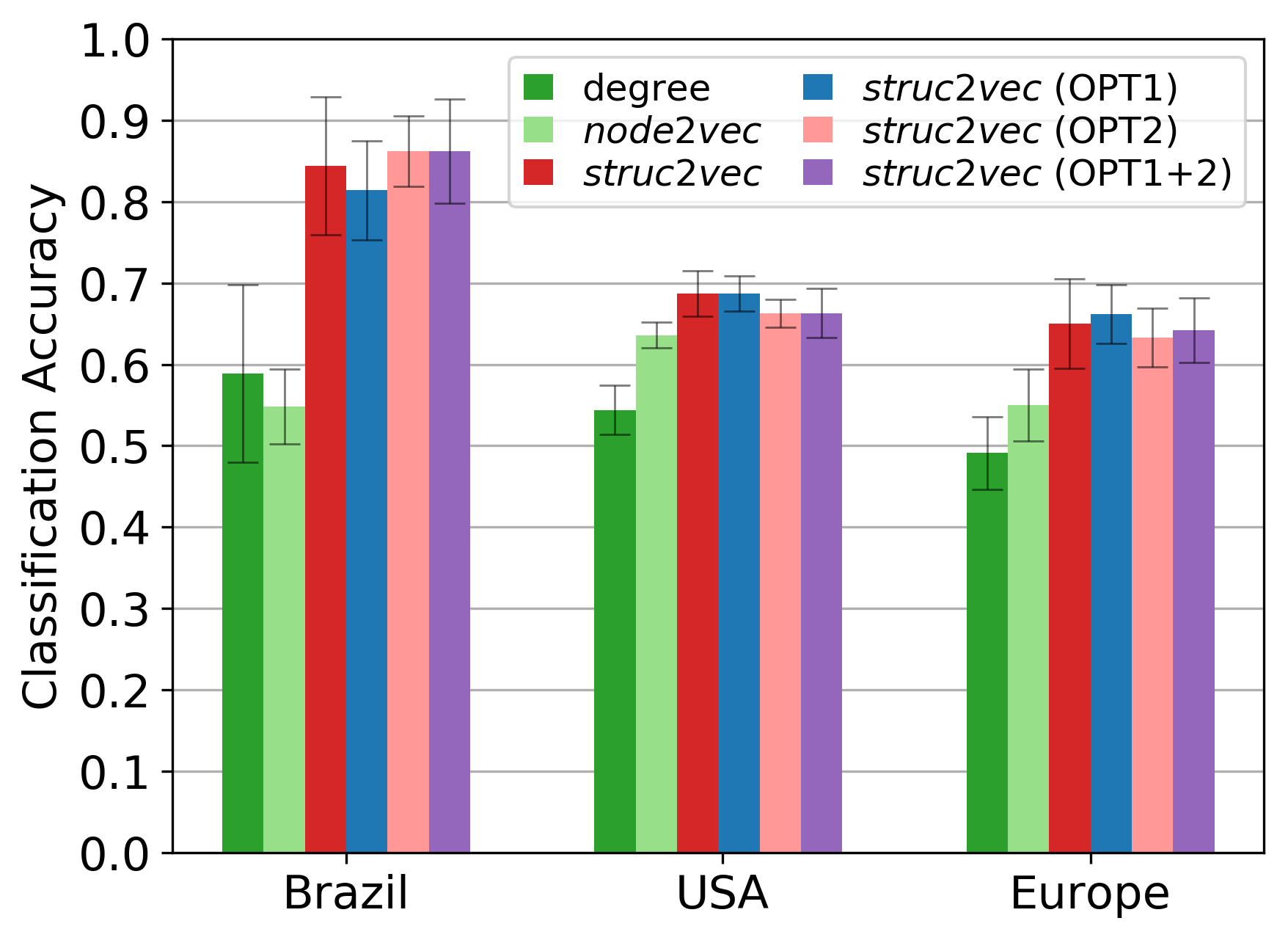
struct2vec 算法的高可拓展性:
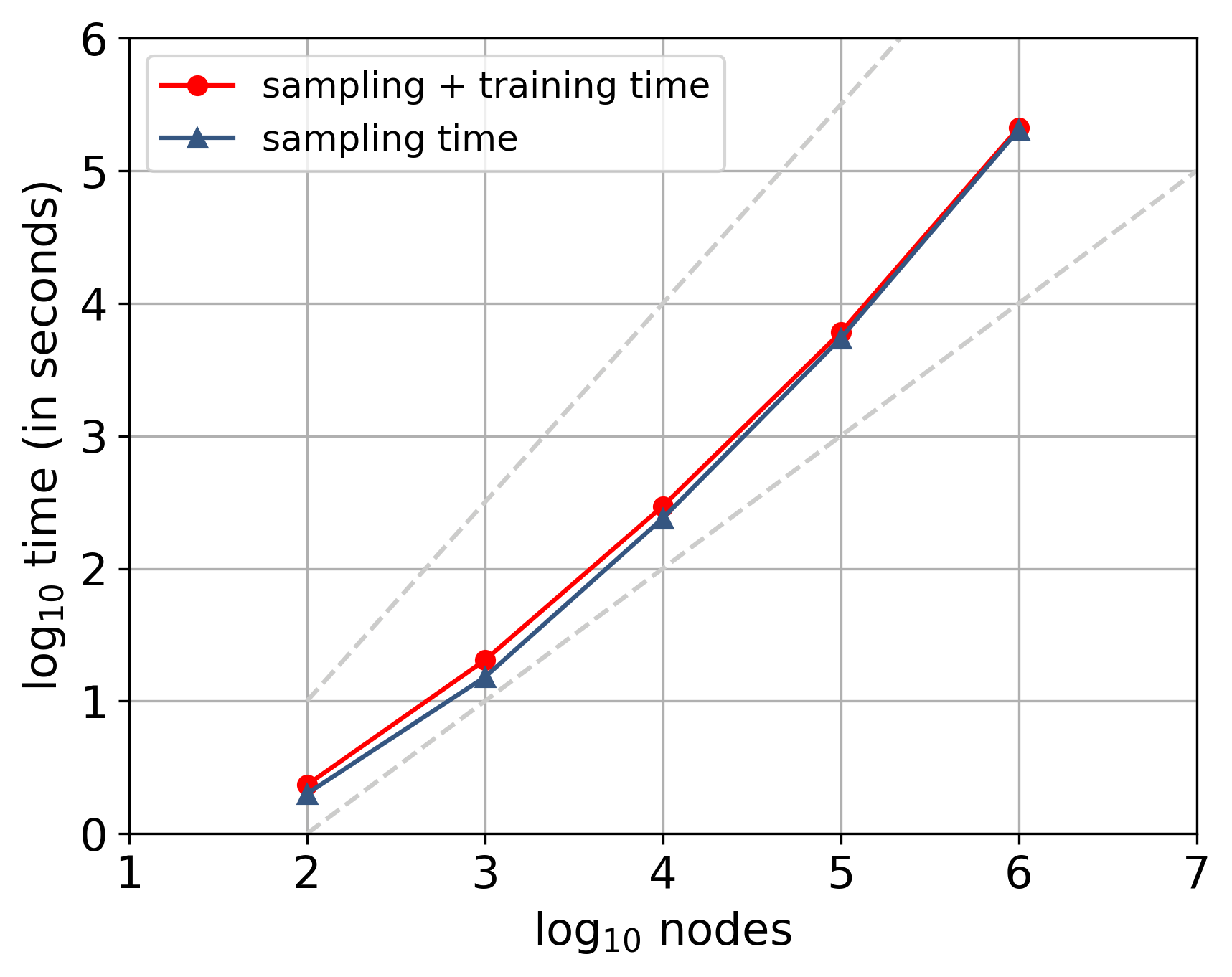
其他实验总结:
- struct2vec 在多种数据集上表现出了很强的结构等价性的捕捉能力
- 面对结构性噪声(随机删除边),struct2vec 表现出较强的鲁棒性
相关资源
- 论文在线地址
- 项目源码地址
- 本地文件地址:Ribeiro et al_2017_istruc2vec-i.pdf
- 本地Zotero地址:Ribeiro et al_2017_istruc2vec-i.pdf