强化学习的定义
强化学习(reinforcement learning,RL)
- RL 是 Agent 通过动作与环境交互,从而实现特定目标最优化的一种计算方法
- Agent 在环境状态为 $S_{t}$ 的情况下产生一个动作决策 $A_{t}$,并将 $A_{t}$ 作用到环境中
- 然后环境发生相应的改变,并将相应的奖励反馈 $R$ 和下一轮状态 $S_{t+1}$ 传回机器
- 以上交互是迭代进行的,目标是最大化在多轮交互过程中获得的累积奖励的期望
强化学习的三个基本要素:
- 状态 $S$,Agent 需要能感知当前环境的状态;比如 AlphaGo 需要了解当前棋盘情况
- 动作 $A$,Agent 需要根据状态和目标,产生能够与环境交互的动作,是不同 Agent 策略的最终体现;比如 AlphaGo 针对当前的棋盘决定下一颗落子的位置
- 奖励 $R$,环境根据当前状态和 Agent 动作,给出可量化的奖励反馈;奖励是评估 Agent 策略的方式,也是指导 Agent 改进的核心目标;比如围棋博弈是否胜利
强化学习的五个关键要素:
- 策略 $\pi$,Agent 会根据策略 $\pi$ 来选择动作;最常见的策略表示方式为条件概率分布 $\pi(a|s)$,即状态 $s$ 时采取动作 $a$ 的概率,此时Agent 会根据最大条件概率原则来选择动作
- 状态转化模型 $P(s′,s,a)$,,描述了状态 $s$ 下采取动作 $a$ 导致状态转移为 $s′$ 的概率
- 奖励衰减因子 $\gamma$,将未来的奖励折算为即时奖励时的折扣因子(未来奖励贴现)
- 动作价值 $v_{\pi}(s)$,表示给定状态 $s$ 和策略 $\pi$ 的情况下采取动作后的价值;动作价值一般及时性更强,但价值不高(比如下棋时的吃子价值);而奖励则一般更滞后,但延迟奖励很高(最终围棋博弈胜利)
- 探索率 $\epsilon$,在训练选择最优动作时,会有一定的概率 $\epsilon$ 不选择使当前轮迭代价值最大的动作,而选择其他的动作;该方式能够保证模型进行更充分的探索,积累足够的历史经验用于学习
强化学习的分类
强化学习是和监督学习,非监督学习并列的第三种机器学习方法
- 有监督学习的目的是寻找一个模型,使其在给定数据分布下得到的损失函数的期望最小
- 强化学习的目的是寻找一个 Agent 策略,使其在与动态环境交互的过程中产生最优的数据分布,即最大化该分布下一个给定奖励函数的期望
在线策略算法 VS 离线策略算法
- 行为策略(behavior policy)用于动作选择,目标策略(target policy)用于价值函数更新
- 在线策略(on-policy)算法表示行为策略和目标策略是同一个策略,比如 SARSA 算法
- 而离线策略(off-policy)算法表示行为策略和目标策略不是同一个策略,比如 Q-Learning
- 对于在线策略,当策略被更新后,采样得到的样本就被放弃了,无法复用(水龙头洗手)
- 对于离线策略,则可以重复利用采样得到的样本,更好地利用历史数据(用脸盆接水后洗手)
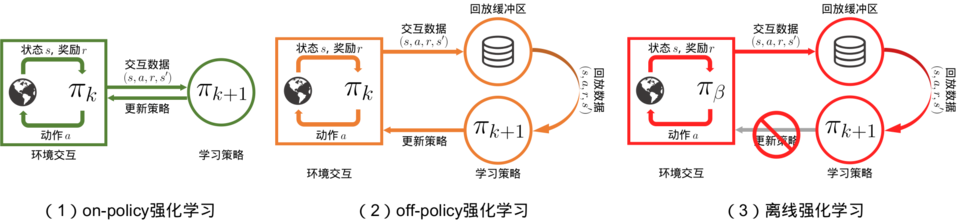
尽管离线策略(off-policy)学习可以让 Agent 基于经验回放池中的样本来学习,但需要保证 Agent 在学习的过程中可以不断和环境进行交互,将采样得到的最新的经验样本加入经验回放池中 如果不允许智能体在学习过程中和环境进行持续交互,而是完全基于一个给定的样本集来直接训练一个策略,这样的学习范式被称为离线强化学习(offline reinforcement learning)
基于模型的强化学习 VS 无模型的强化学习
- 此处“模型”指的是环境模型,即对环境的状态转移概率和奖励函数进行建模
- 无模型的强化学习(model-free reinforcement learning)主要依赖 Agent 与环境交互采样到的数据直接进行策略提升或者价值估计,比如蒙特卡洛法或时序差分算法 TD
- 基于模型的强化学习(model-based reinforcement learning)则会先根据 Agent 与环境交互采样到的数据学习环境模型,然后进行策略提升或者价值估计,比如 Dyna 算法框架
- 基于模型的强化学习一般不单独使用,而是和无模型的强化学习结合起来;基于模型的强化学习的主要作用是降低对真实环境的样本需求量,但环境模型无法完全代替真实环境,因此其期望回报一般低于无模型的强化学习
基于价值的强化学习 VS 基于策略的强化学习
- 前文介绍的时序差分算法 TD 或 DQN 都是基于价值(Value Based)的强化学习,这类算法的最优策略一般是确定性策略(先学习值函数,再寻找价值最大化对应的策略),不适用于连续动作空间或受限状态下的问题
- 基于策略(Policy Based)的强化学习,将策略表示为一个连续的函数并进行策略函数的优化,其核心点在于策略的参数化和优化;策略梯度算法是基于策略的方法的基础
- 还有一类将策略和价值相结合的算法,比如 Actor-Critic 算法