天使问题是由英国数学家约翰·何顿·康威提出的一个博弈论问题,在 2006 年已获解答。
天使问题是关于一个叫天使与恶魔的双人游戏,其规则如下:
- 两名玩家分别扮演天使和恶魔
- 游戏开始前,指定一个正整数 K,称之为天使的力量
- 游戏在一个无限大的方格棋盘上进行;开始时棋盘是空的,天使停留在棋盘上的某一个方格(称为天使的起始点),恶魔并不存在于棋盘上
- 每一轮中,恶魔可以在棋盘上放置一个路障,路障不可以放置在天使停留处
- 每一轮中,天使可以向相邻格移动至多 K 步,移动过程中可以穿过路障,但移动终点必须停留在没有路障的格中;纵横斜格均算作相邻格
- 从恶魔开始,双方交替进行(若从天使开始,从上面的规则描述,亦可等价转换为从恶魔开始的局面)
- 若在一轮中,天使无法移动,则恶魔获胜
- 如果天使能够无限地继续游戏,则天使获胜
天使问题可以陈述为:是否存在某个 K,使得力量为 K 的天使拥有必胜策略?
天使问题图示:
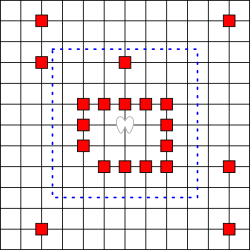
- 图中棋盘区域中央为天使,当天使力量为 3 时,其当前可移动区域被蓝色点画线围起
天使问题的已知证明(恶魔必胜策略)
- K = 1 时,恶魔有必胜策略(康威, 1982)
- 如果天使不可以降低其 y 坐标,则恶魔有必胜策略(康威, 1982)
- 如果天使一直增加它到起始点的距离,则恶魔有必胜策略(康威, 1996)
天使问题的已知证明(天使必胜策略)
- 在 2006 年,有 4 位数学家独立解决了天使问题
- 皮特·加茨(Péter Gács)证明了当 K 充分大时,天使有必胜策略
- 英国数学家布莱恩·鲍迪奇(Brian Bowditch) 证明了 K = 4 的时候,天使有必胜策略
- 挪威数学家 Oddvar Kloster 和 András Máthé 各自证明了 K = 2 的时候,天使有必胜策略