生存分析模型
发表评论
19 views

生存分析入门

生存分析（Survival analysis），也称失效分析

  • 分析距离特定事件发生前的预期持续时间，例如生物体的死亡和机械系统的失效
  • 起点/起始事件（initial event）：反应生存时间起始特征的事件，如疾病确诊、治疗开始等。
  • 结局/失效事件（failure event）：研究规定的终点结局，比如患者死亡、治疗的结束等
  • 生存时间，起点事件到结局事件之间所经历的时间（也可以是距离等度量方式）
  • 中位生存期/半数生存期：50%个体存活的情况所对应的生存时间

起始事件和失效事件是相对应，并且可应用于不同行业；比如在互联网行业中，起始事件可以是用户开始活跃和用户流失，那生存分析模型就可以用于预测用户流失的概率

生存时间的分布通常不服从正态分布，而是呈现出偏态分布的特征，常见的分布形式包括指数分布、Weibull 分布、Gompertz 分布以及对数 logistic 分布等

删失/截尾（Censoring）是影响生存时间数据完整性的重要因素

  • 删失，由于起点事件或结局事件缺失，导致生存时间不可知
  • 截尾，样本的分布是有偏的，比如观察样本提前退出，或超出观测区间

生存函数（Survival Function）

  • 也称为积累生存函数/概率（Cumulative Survival Function）或生存率，符号$S(t)$
  • 生存函数表示观察对象生存时间越过时间点t的概率，$t=0$ 时生存函数 $S(t)=1$
  • 一般随着时间推移，生存函数值会单调递减；对应的函数曲线也被称为生存曲线

风险函数（Hazard Function）

  • 累积风险函数 $H(t)=-\log(S(t))$；累积分布函数 $F(t)=1-S(t)$；概率密度函数 $f(t)=F'(t)$
  • 风险函数表示生存时间达到 $t$ 后瞬时发生失效事件的概率，符号 $h(t)=f(t)/S(t)$

常见的单因素生存分析方法：Kaplan–Meier 曲线

常见的多因素生存分析方法：Cox 比例风险回归

Kaplan–Meier 分析

Kaplan Meier 分析，又称 K-M 分析

  • 可用于研究1个因素对于生存时间的影响，在医疗领域中使用广泛
  • 由 Kaplan 和 Meier 与1958年共同提出的一种单因素生存分析方法

K-M 分析步骤

  1. 数据整理：确保每个样本观测区间与事件的完整性
  2. 划分时间区间，并按区间依次计算生存概率
  3. 对区间生存概率进行逐段累乘，并绘制 K-M 生存曲线
  4. 为 K-M 曲线添加 95%的置信区间，以反映估计准确率

K-M 分析过程中，对于在研究结束前未发生事件的参与者（右侧删失），他们将被纳入到最后一个已知时间区间的生存率计算中，但在此之后不再影响生存率的计算

K-M 曲线示例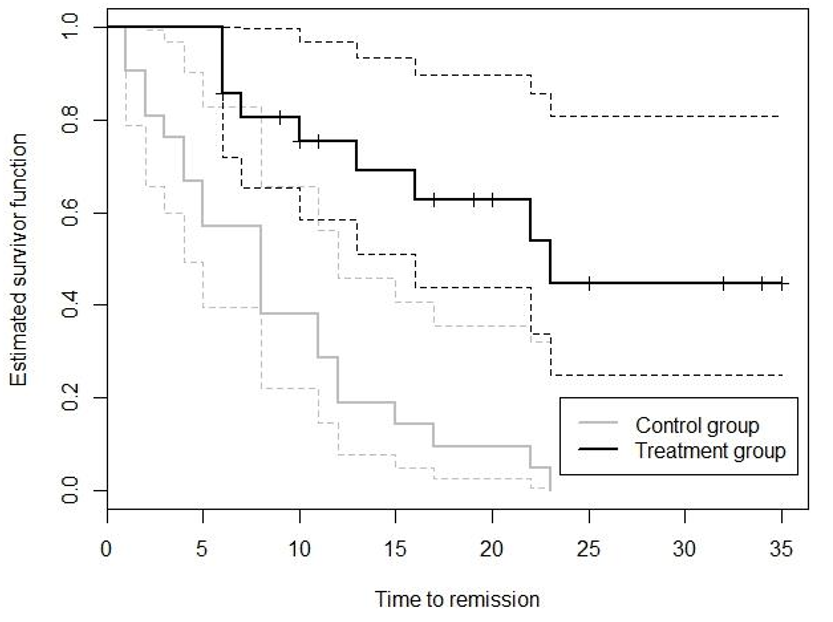： K-M 曲线对比：

  • 目的：判断两组间整体生存时间分布是否存在统计学差异
  • 一般有三种常见的卡方检验方法来判断差异，具体区别可参见下表
检验方法 假设检验方法 检验类型 自由度 权重 影响
Log-rank 检验 卡方检验 同 组数-1 各时点均为 1 对远期效应敏感
Breslow 检验 卡方检验 异 组数-1 各时点存活例数 对近期效应敏感
Tarone-Ware 检验 卡方检验 异 组数-1 各时点存活例数（平方根） 介于两者之间

K-M 分析总结

  • 一种非参数单因素方法，适用情况广泛，不受分布假设的限制
  • 随着样本的增加，K-M 曲线将逐渐逼近真实经验生存曲线
  • 直观展示随时间变化的生存率，能够处理右侧删失数据的情况

Cox 比例风险回归

Cox 比例风险回归模型，简称 Cox 回归 $$h(t, X)=h_0(t)\times\exp(b_1x_1+b_2x_2+…+b_px_p)$$

  • 由 Cox 于1972年提出的半参数模型，其公式如上所示
  • 其中 $t$ 为生存时间，$h(t)$ 是不同时间的风险值（Hazard）
  • $x_{1},x_{2},...,x_{p}$ 是具有预测效应的协变量，每个变量对应的效应为 $b$
  • $h_{0}(t)$ 是基准风险函数，描述了其他协变量都为 0 或均值时对应的风险值
  • $h_{0}(t)$ 可根据不同的数据来选择不同的分布，因此是模型中的非参数部分
  • $\exp(b_px_p)$ 则是模型的参数部分，其对风险值是乘性效应；当 $\exp(b_px_p)=1$ 时，表示该因素对事件风险无影响；当 $\exp(b_px_p)>1$ 时，表示 $x_{p}$ 是危险因素；当 $\exp(b_px_p)<1$ 时，表示 $x_{p}$ 是保护因素

Cox 回归的一般过程：

  1. 数据准备，确定包含协变量、生存时间和结局事件的数据集
  2. 假设检验，使用 Schoenfeld 残差法 (Schoenfeld Residuals) 来判断某个变量的残差与时间是否存在显著相关性（P < 0.05），如果存在相关性则说明不满足 Cox 回归的前提假设
  3. 筛选合理的协变量并通过最大化偏似然函数来计算回归系数
  4. 对回归结果进行结果并添加回归系数的假设检验结果与 95%置信区间
  5. 估计基准风险 $h_{0}(t)$，并用于生存函数的估计和生存预测概率：

$$S(t) = S_0(t)^{exp(\Sigma b_i \times x_i)} = (exp(-H_{0}(t)))^{exp(\Sigma b_i \times x_i)}=exp(-\Sigma_{j=0}^{j=t}h_{0}(j))^{exp(\Sigma b_i \times x_i)}$$

  • 时刻 $t$ 的生存率 $S(t)$，是基准生存率 $S_0(t)$ 的风险倍数累乘
  • 利用生存分析中的恒等式 $S(t)=e^{-H(t)}$ 可实现风险与生存率的互换
  • 时刻 $t$ 基准风险 $H_{0}(t)$ 是多个历史瞬时风险的累加，$H_{0}(t)=\Sigma_{j=0}^{j=t}h_{0}(j)$
  • 瞬时基准风险常用Breslow 估计法： $h_0(j)=\frac{d_j}{\sum_{k=1}^{K}{} exp({ b_i \times (X_k-\bar{X_k}))}}$；其中分子表示时刻 $j$ 的发生事件的个体数；分母表示时刻 $j$ 所有风险个体的协变量线性组合指数的和

当 Cox 回归用于探索风险/保护因子时，不需要估计基准风险 当 Cox 回归用于预测时，需要估计基准风险以及后续生存概率

Cox 回归的评估指标：C-index/AUROC、RMSE、MAE 等

参考：

Wikipedia - Survival analysis
Wikipedia - Kaplan–Meier estimator
深入解析KM图（Kaplan-Meier图）
生存分析的背景及理论知识
生存分析入门之三（一文读懂 Cox 比例风险回归模型）
生存分析从概念到实战
生存分析中的半参数模型：Cox 回归模型

往年同期文章