前置知识:因果推断
1 因果关系介绍
因果 DAG(有向无环图):使用图来表示因果关系
用于决策干预的链路预测任务(比如搜索或推荐)往往是存在因果关系的
因果关系在决策中的示例:
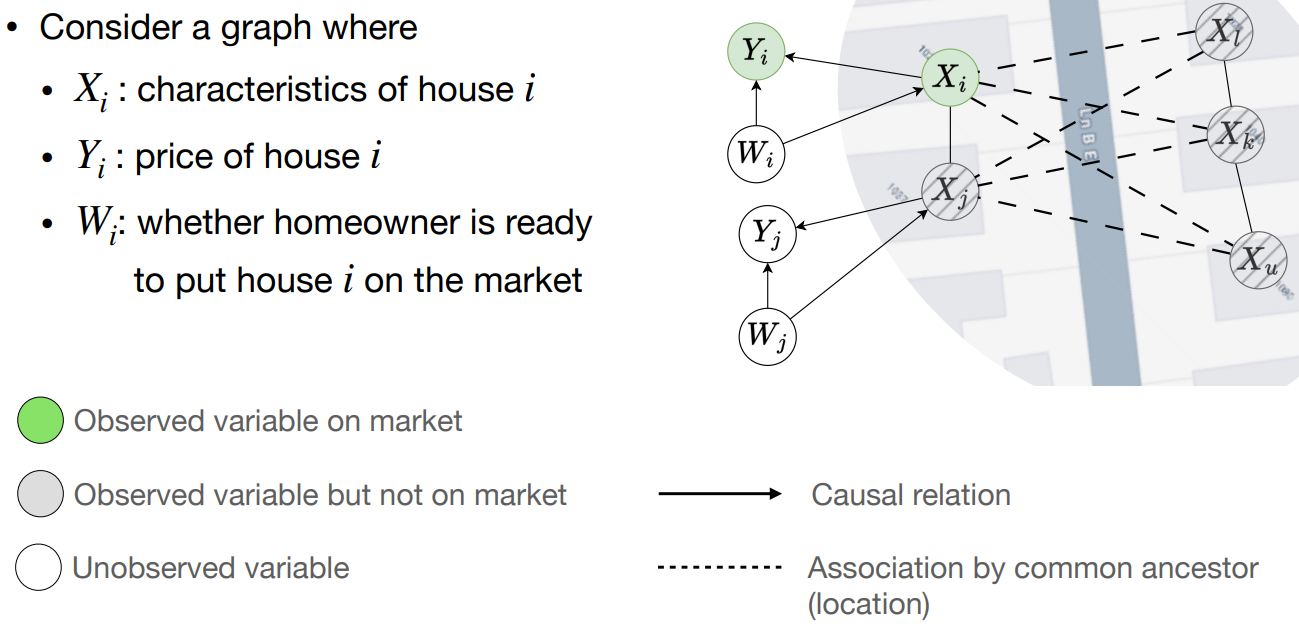
- 上图中,$X_i$ 表示第 $i$ 个房子的特征,$Y_i$ 表示第 $i$ 个房子的价格,$W_i$ 表示房主是否准备出售房子;实线表示因果关系,虚线表示由父节点决定的相关性
- 一般情况下,模型可以根据市场上的待售房屋的信息和报价,来预估个人的房屋价格;但实际应用时,房主的出售行为 $W_i$ 是房屋属性 $X_i$ 和价格 $Y_i