分类目录归档：课程
已知三角形面积的计算公式为$S=\frac{1}{2}absin\theta$
则由向量$\vec{A}$和$\vec{B}$组成的平行四边形面积为$S=|\vec{A}||\vec{B}|sin\theta$
设$\vec{A'}$为向量$\vec{A}$逆时针旋转$90°$的结果，$\vec{A'}$与$\vec{B}$的夹角为$\theta'=\frac{\pi}{2}-\theta$
则平行四边形面积为$S=|\vec{A'}||\vec{B}|cos\theta'=\vec{A
向量$\vec{A}$主要由长度$|A|$和方向$dir(A)$组成，起点和终点不固定
$$\vec{A}\cdot \vec{B}=\Sigma a_ib_i=|\vec{A}||\vec{B}|cos\theta$$ 点乘的结果是一个常数，同时包含了向量长度信息和夹角信息
点乘的证明（基于向量版余弦定理）：
- 定义向量$\vec{A}$和向量$\vec{B}$，量向量夹角为$\theta$
- 定义向量$\vec{C}=\vec{A}-\vec
山东寿光农村人，家里种大棚，虽然现在在外面上大学，从五岁开始就干农活下地，对农活还比较了解，各种下地干的活都拿得出手。 对农业最深刻的印象就是 累，收益效益低 简单描述一下现在蔬菜大棚农民的劳作 各种蔬菜，得益于现在北方的冬暖式大棚技术发展，无论冬夏，各种季节都能种 ，因而所谓的农闲 ，其实只有夏天最热的那会到现在 ，也是要去棚地里推粪 ，修整耕地。 拿黄瓜举个例 ，黄瓜这个东西可以说是最累人的作物之一 ，从种植开始 ，到第一茬收获，这段时间其实还是最简单的 ，你只需要每天定时通风 ，每隔两天浇一次水 ，每隔两三日打一次药 。 可不要以为简单 ，想这个谁不会 ，你要面对的可是数以万计的黄瓜
山西大同人。 父亲是一名大货车司机。 我小时候住在城郊一个叫时庄的村子，整个村很多都在养大车，就是拉煤。那时候养大车赚的特别多，05-06年每个月赚几万的比比皆是，那时候的时庄人看不起城里人，孩子们初中都念不完就开始跟车，学车，跑车，赚钱。 人们有了钱，也没有文化，吃喝嫖赌是常态。 整个村子就没几个正经大学生，我印象中就十来个吧，我因为有个好妈妈，侥幸成了其中之一。 不光是时庄，那时候整个大同矿区都是这种风气，矿工下井一个月赚一万，吃香的喝辣的，也不重视子女教育，大不了孩子大了花钱找人当两年bing，回来矿上分配工作。这就是那时候大同人的常态。 所以作为一个大同人，我对资源诅咒这四个字的理
Unit 1 知识点简单概
（最后一节课换了个导师，所以教学进度衔接似乎不太好 = =）
幂级数的性质1：存在收敛半径$R$ 幂级数的性质2：当$|x|<R$时，$f(x)$可无限求导（比如说多项式级数）
泰勒展开式：
$$f(x)=\Sigma_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n$$
示例1：几何级数 geometric series $\frac{1}{1+x}=1-x+x^2-x^3...(R=1)$
示例2：$ln(1+x)=\int_0^x\fr
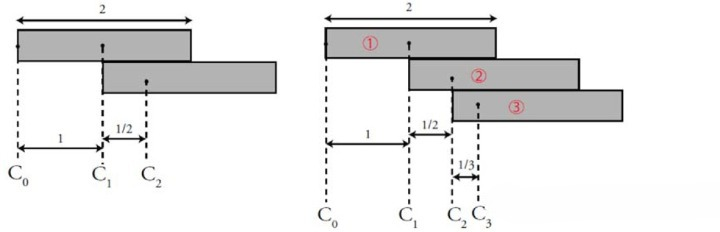
将1号木板放置在桌面边缘，在木板不掉落的情况下不断探出；然后再叠加2号木板，追求总探出长度最大的情况，以此类推，判断最终总长度是否是有限的
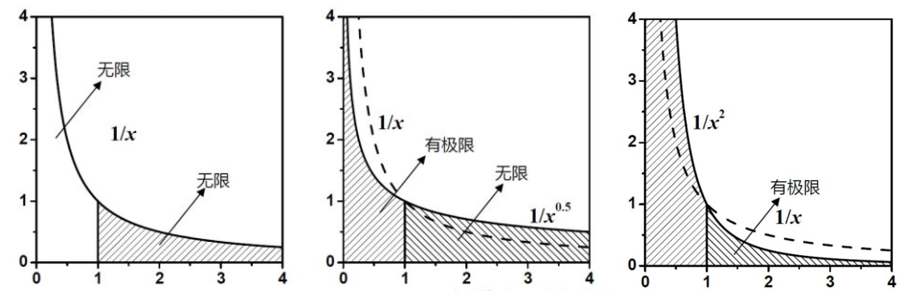
反常积分的第二种情况就是积分区域内有奇点的情况
示例：讨论$\int_0^1\frac{dx}{x^p}$的收敛性
总结3 反常积分示例中示例3的结果可得到以下结果：
芝诺悖论：$1+\frac{1}{2}+\frac
$$\begin{equation}
IF = \left\{
\begin{array}{rl}
f(x)\to \infty \\ \\
g(x)\to \infty \\ \\
\frac{f'(x)}{g'(x)}\to L
\end{array} \right.
\end{equation}
\ \ \ AS \ \ x\to a \ \ THEN \ \frac{f(x)}{g(x)}\