分类目录归档：基础数学
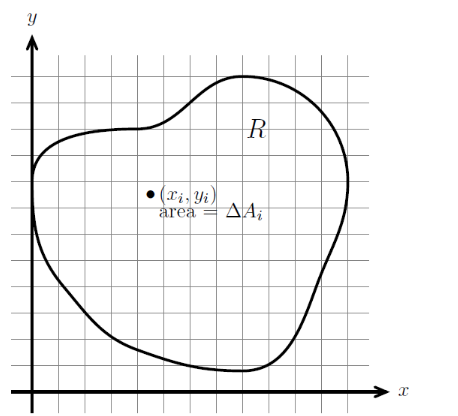
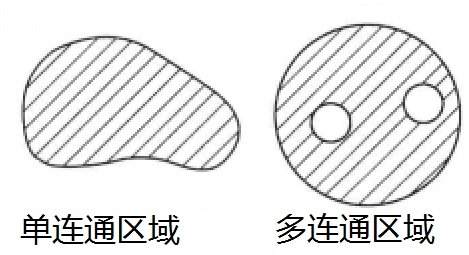
单连通区域$R$：由单一的一块组成的区域$R$，即没有“洞”的区域
要求：对于单连通区域$R$内存在的任意闭合曲线$C$，曲线$C$的区域也属于$R$
不满足以上要求的区域则被称为多连通区域，或复连通区域
在之前第21节课中曾提及判定梯度场的前提条件，即$\vec{F}$处处有定义可导。在了解单连通区域的定义后，可以发现此前提条件等价于$\vec{F}$的定义域是单连通区域：
如果$\vec{F}$的旋度是0，且$\vec{F}$的定义域是单连通区域，则$\vec{F}$是保守场/梯度场
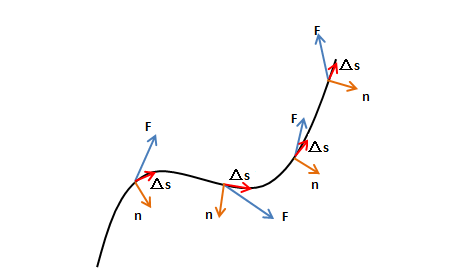
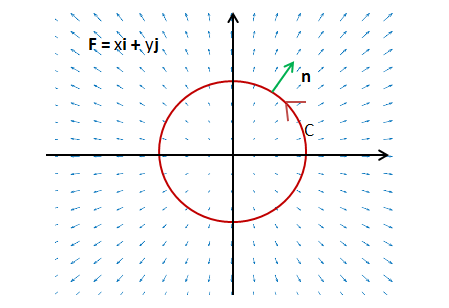假设$C$为逆时针的封闭曲线，包围着区域$R$；如果向量场$\vec{F}$在曲线$C$和区域$R$处处有定义且处处可微，则存在格林公式使得线积分转化为双重积分： $$∮_c\vec{F}\cdot d\vec{r}=\int \! \! \!\int_Rcurl(\vec{F})dA$$ 坐标形式的格林公式： $$∮_cMdx+Ndy=\int \! \! \!\int_R(N_x-M_y)dA$$
此处限制曲线$C$为逆时针是一种人为规定的方向，也就是一种约定成俗。就好像定义旋度$=N_x-M_y$，而不
上一节对于向量场判断是否为梯度场已有较为全面的表述
本小节将从梯度场的性质出发，展示最常见且便捷的判断方法
如果$\vec{F}$是梯度场，则$\vec{F}=\nabla f,M=f_x,N=f_y$
由$f_{xy}=f_{yx}$可知，梯度场$\vec{F}$需要满足：$M_y=N_x$
- $\vec{F}$是梯度场，是$M_y=N_x$的充分不必要条件
- $M_y=N_x$在$\vec{F}$处处有定义可导的前提下，可推得$\vec{F}$是梯度场
- 在后续的第24节课中将提及，这
向量场（vector fields）将空间中的点映射为向量，用于描述空间流体或力的强度和方向
常见的向量场举例：风场、引力场、电磁场、水流场
假设存在函数$M(x,y)$和$N(x,y)$，用$\vec{F}$来描述向量场： $$\vec{F}=M\vec{i}+N\vec{j}$$ 示例1：$\vec{F}=2\vec{i}+\vec{j}$，其向量场可视化结果如下：
示例2：$\vec{F}=x\vec{j}$，其向量场可视化结果如下：
示例3：$\vec{F}=-y\vec{i}+x\vec{j}$，其向量场可视化结果
在上一节中，从直角坐标系到极坐标的转换其实是一种换元法的特例： $$\int\int_Rf(x,y)dA=\int\int_Rg(r,\theta)rdrd\theta$$
在本小节，对这类方法进行拓展，并以例题的形式对变量替换法（换元法）进行说明
例题：计算$(\frac{x}{a})^2+(\frac{y}{b})^2=1$椭圆面积
分析：考虑借助$u=\frac{x}{a},v=\frac{y}{b}$进行换元
- 此时可得微分关系：$du=\frac{1}{a}dx,dv\frac{1
例题：计算二重积分$\int\int{1-x^2-y^2}dA$，限定区域在$x^2+y^2<1,x\geq 0,y\geq 0$
分析：考虑$sin^x+cos^2=1$的特性，极坐标化将极大简化运算过程
- 对变量进行极坐标化，带入$x=rcos\theta,y=rsin\theta$
- 对函数图像进行网格化处理，在笛卡尔坐标系中，函数区域将会细分为多个横平竖直的小矩阵；而在极坐标系中，函数区域将有无数从原点出发的射线与半径不一同心圆（具体结果如下图所示）
- 此时很明显$dr\cdot d\theta
假设存在区域$R$与函数$f(x,y)$，对区域$r$进行网格化分割，其中第$i$块小格的面积为$\Delta A_i$，并且该小格的中心坐标为$(x_i,y_i)$，则函数$f$在区域$R$内的二重积分可表示如下： $$\int \! \! \!\int_{R} f(x,y)dA=\int \! \! \!\int_{R} f(x,y)dA$$ 其中，$dA$可以看作$dx$与$dy$的乘积（小格子都被近似看作为矩阵）
考虑单变量积分，其积分值表示函数曲线在特定区间下围绕产生的面积值。
同理，二重积分的几
截止到第十五节课，本课程的第二单元：偏微分（Unit 2 Partial derivatives）部分内容已完成，内容脉络简单梳理如下：
$$∮_