分类目录归档：基础数学
方程$ax+by+cz=d$定义了一个平面，此方程的矩阵形式如下： $$\left[ \begin{matrix} a \\ b \\ c \\ \end{matrix} \right] \cdot \left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right] =d$$ 上面的式子也可以整理如下： $$\left[ \begin{matrix} a \\ b \\ c \\
已知三角形面积的计算公式为$S=\frac{1}{2}absin\theta$
则由向量$\vec{A}$和$\vec{B}$组成的平行四边形面积为$S=|\vec{A}||\vec{B}|sin\theta$
设$\vec{A'}$为向量$\vec{A}$逆时针旋转$90°$的结果，$\vec{A'}$与$\vec{B}$的夹角为$\theta'=\frac{\pi}{2}-\theta$
则平行四边形面积为$S=|\vec{A'}||\vec{B}|cos\theta'=\vec{A
向量$\vec{A}$主要由长度$|A|$和方向$dir(A)$组成，起点和终点不固定
$$\vec{A}\cdot \vec{B}=\Sigma a_ib_i=|\vec{A}||\vec{B}|cos\theta$$ 点乘的结果是一个常数，同时包含了向量长度信息和夹角信息
点乘的证明（基于向量版余弦定理）：
- 定义向量$\vec{A}$和向量$\vec{B}$，量向量夹角为$\theta$
- 定义向量$\vec{C}=\vec{A}-\vec
Unit 1 知识点简单概
（最后一节课换了个导师，所以教学进度衔接似乎不太好 = =）
幂级数的性质1：存在收敛半径$R$ 幂级数的性质2：当$|x|<R$时，$f(x)$可无限求导（比如说多项式级数）
泰勒展开式：
$$f(x)=\Sigma_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n$$
示例1：几何级数 geometric series $\frac{1}{1+x}=1-x+x^2-x^3...(R=1)$
示例2：$ln(1+x)=\int_0^x\fr
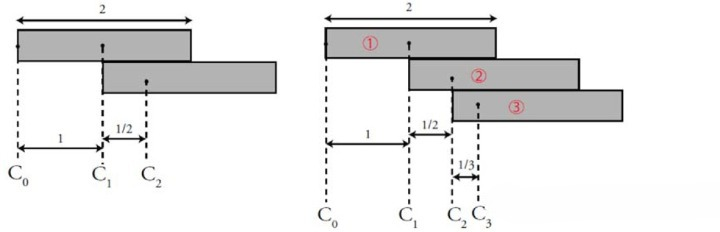
将1号木板放置在桌面边缘，在木板不掉落的情况下不断探出；然后再叠加2号木板，追求总探出长度最大的情况，以此类推，判断最终总长度是否是有限的
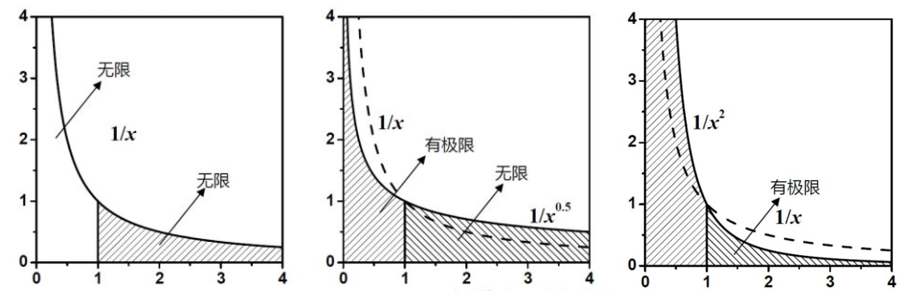
反常积分的第二种情况就是积分区域内有奇点的情况
示例：讨论$\int_0^1\frac{dx}{x^p}$的收敛性
总结3 反常积分示例中示例3的结果可得到以下结果：
芝诺悖论：$1+\frac{1}{2}+\frac
$$\begin{equation}
IF = \left\{
\begin{array}{rl}
f(x)\to \infty \\ \\
g(x)\to \infty \\ \\
\frac{f'(x)}{g'(x)}\to L
\end{array} \right.
\end{equation}
\ \ \ AS \ \ x\to a \ \ THEN \ \frac{f(x)}{g(x)}\
洛必达法则（L'Hopital's Rules）：当$f(a)=g(a)=0$
$$lim_{x\to a}\frac{f(x)}{g(x)}=lim_{x\to a}\frac{f(x)/(x-a)}{g(x)/(x-a)}=\frac{f'(x)}{g'(x)}(g'(x)\neq0)$$
$$lim_{x\to 0}\frac{sin5x}{sin2x}=lim_{x\to 0}\frac{5cos5x}{2cos2x}=\frac{5}{2}$$
$$lim_{x\to 0}\frac{cosx-