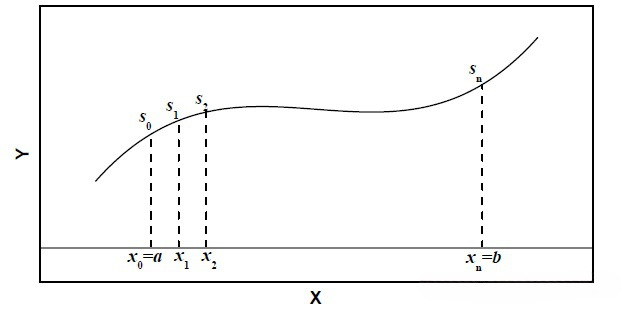
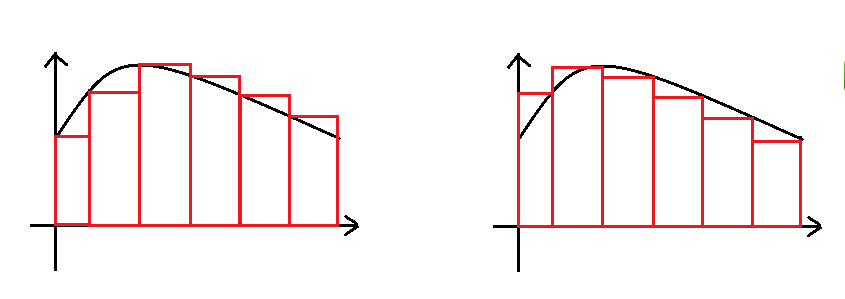
1 极坐标与面积
半径为$a$的圆的面积为$A=\pi a^2$
其中角度为$\Delta \theta$的扇形面积为$\Delta A$,则$\Delta A=\frac{\Delta \theta}{2\pi}\pi a^2=\frac{1}{2}a^2\Delta \theta$
无限细分角度,可得$dA=\frac{1}{2}a^2d\theta$,则$A=\int_{\theta_1}^{\theta_2}\frac{1}{2}a^2d\theta$
对于一些不规则的类圆图形,可引入参数方程,