个人笔记

1 曲线构图补充

画图法步骤：

1. 描点

• 不连续点（特别是$f(x)\to \mathrm{\infty }$的点）
• 无限远端（$x\to \mathrm{\infty }$）
• 易求的点

2. 求驻点$f^{\prime }(x)=0$，判断不同区域一阶导数的正负性，检验单调性
3. 求拐点$f^{″}(x)=0$，判断不同区域二阶导数的正负性，检验凹凸性
4. 画图和总结

练习：$f(x)=\frac{1+x}{2+x}$绘图

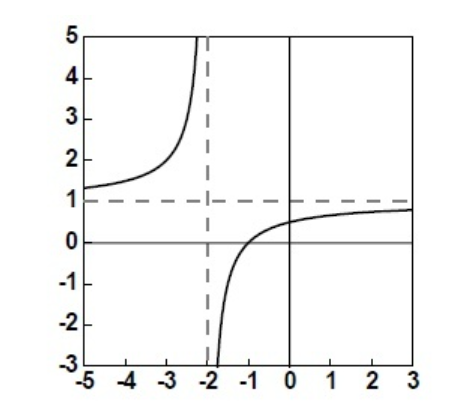
2 最值问题

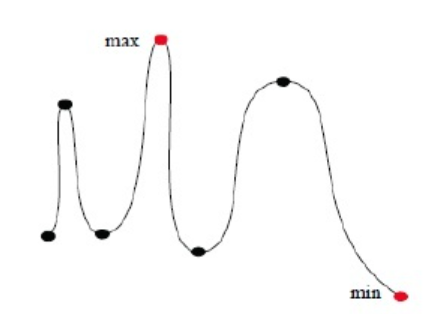
分析函数极值点关键是找到驻点、边界点和不连续点

3 参考

MIT—单变量微积分笔记11 极值问题

#最值

Read more

1 线性近似和二阶近似补充

$$\underset{k\to \mathrm{\infty }}{lim}{a}_k=\underset{k\to \mathrm{\infty }}{lim}(1+\frac{1}{k}{)}^k=e$$

利用线性近似进行更简单的证明

• $ln(a_k)=k\times ln(1+\frac{1}{k})\approx k\times \frac{1}{k}=1$

二阶近似的性质

• $ln(a_k)=k\times ln(1+\frac{1}{k})\approx k\times (\frac{1}{k}-\frac{1}{2k^2})=1-\frac{1}{2k}$
• $

Read more

1 线性近似 linear approximation

$$f(x)\approx f(x_0)+f^{\prime }(x_0)(x-x_0)$$

• 其中$\approx$仅在$x$接近$x_0$时成立

以$x_0=0$且$x\approx 0$为前提，几种常见的函数线性近似：

• $sin(x)\approx x$
• $cos(x)\approx 1$
• $e^x\approx 1+x$
• $lm(1+x)\approx x$
• $(1+x)^r \a

Read more

1 多项式导数的推广

$$\frac{d}{dr}{x}^r=r{x}^{r-1}$$ 其中$r\in$实数

快速证明 $$\frac{d}{dr}{x}^r=\frac{d}{dr}{e}^{ln(x^r)}=e^{ln(x^r)}\times r\times \frac{1}{x}=r{x}^{r-1}$$

2 自然对数的常见应用

股票指数，以FTSE100为例

• FTSE100全称为伦敦金融时报100指数，简称英国富时100指数
• 欧洲三大股票指数包括：30工业股、FT-100、综合

Read more

1 指数（exponential）的导数Part1

$$\frac{d}{dx}{a}^x=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{a^{x+\mathrm{\Delta }x}-a^x}{\mathrm{\Delta }x}=a^x\underset{\mathrm{\Delta }x\to 0}{lim}\frac{a^{\mathrm{\Delta }x}-1}{\mathrm{\Delta }x}=M(a)a^x$$

• 其中$a$表示某一固定常数，$M(a)$表示某一固定函数值
• 当$x=0$时，$M

Read more

1 隐函数微积分

扩展$(x^n{)}^{\prime }=n{x}^{n-1}$为$(x^a{)}^{\prime }=a{x}^{n-1}$

• 其中$a$表示有理数，可以用$\frac{m}{n}$表示
• $m,n\in Z$，即$m$和$n$属于整数集

扩展公式的证明：

• 转换$y=x^{\frac{m}{n}}$为$y^n=x^m$
• 由此可得$\frac{d}{dx}{y}^n=\frac{d}{dx}{x}^m=m{x}^{m-1}$
• 借助链式法则可得$\frac{d}{dy}{y}^n\frac{dy}{dx}=m{x}^{m-1}$
• 化简可得$\frac{dy}{dx}=\frac{mx^{m-

Read more

1 导数的乘法法则

$(uv{)}^{\prime }=u^{\prime }v+v^{\prime }u$

乘法法则推导Part 1 $$\begin{align} \Delta(uv) & = u(x+\Delta x)v(x+\Delta x)-u(x)v(x) \ \ & = [u(x+\Delta x)-u(x)]v(x+\Delta x)+u(x)[v(x+\Delta x)-v(x)] \ \ & = \Delta u\times v(x+\Delta x)+u(x)\D

Read more

1 求导公式

1. 特定函数求导，如$x^n$的导数为$n{x}^{n-1}$
2. 通用公式，如${(u+v)}^{\prime }=u^{\prime }+v^{\prime }$
3. 以上两种的混合使用

2 三角函数的导数

• 在正式推导前，需要先推导出两个特殊情况下的极限变化率

第一种特殊情况： $$\underset{x\to 0}{lim}\frac{sin(x)}{x}=1$$ 几何法证明：

（图片引用说明：知乎@三少爷的贱男春）

• 上图为一个标准单位圆，角度$\theta$对应弧长为$2\pi r=\theta$
• 随着$\theta$的减少，极短曲线可看作直线，即$\theta=sin(\theta

Read more

1 变化率 rate of change

• 注意：本课前半部分内容为第一节内容未讲完部分。第一节仅描述了导数的几何解释，而变化率则是导数的物理解释。

$$\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{dy}{dx}$$

• $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$表示的是一种平均值
• $\frac{dy}{dx}$表示的是一种瞬时值

Read more

1 何为导数 derivative

• 几何解释 geometric interpretation
• 物理解释 physical interpretation
• 导数全方位的重要性 importance to all measurements

2 如何对已知的任意函数求导

• 思考：如何对$e^{xarctan(x)}$求导

导数的几何解释

• 选择函数曲线上的点$P$，其坐标值为$(x_0,y_0)$
• $x_0$沿着x轴（x-axis）移

Read more