仅搜集收录了部分个人感兴趣的文章,并进行简单记录
1 概念科普
1.1 大语言模型和病历质量下降
2024-11-01 文章链接
- LLM 可能会进一步降低病历中的信息质量。高质量记录绝不是对患者诊疗过程的一般文字转录,而是包含了医师推理、患者价值观以及病历中其他地方可能没有体现的临床背景。
- 使用 LLM 可能会削弱临床推理能力。有观点认为转录诊疗过程和总结病历是相对低风险的 LLM 应用方式,但持
仅搜集收录了部分个人感兴趣的文章,并进行简单记录
2024-11-01 文章链接
幻觉,一种现实世界与幻想世界的边界模糊:
大模型的幻觉问题是不可避免的,是一种先天的局限性

变点检测(Change point detection, CPD)是指在时间序列中发现统计特性发生重大变化的点
变点检测示例(斯匹次卑尔根岛的年均气温趋势):
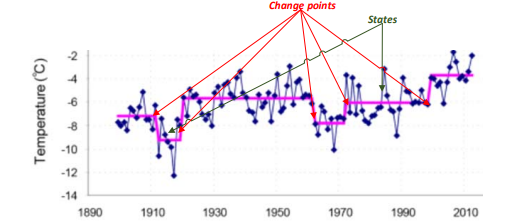
变点检测的分类:
变点检测的有监督方法:
无限猴子定理(英语:Infinite monkey theorem):让一只猴子在打字机上随机地按键,当按键时间达到无穷时,几乎必然能够打出任何给定的文字,比如莎士比亚的全套著作
定理的数学描述:当一个事件(例如,一只猴子输入一组字符)以有限的非零概率在给定的试验中发生时,随着独立试验的数量趋于无穷大,该事件从未发生的概率趋于零
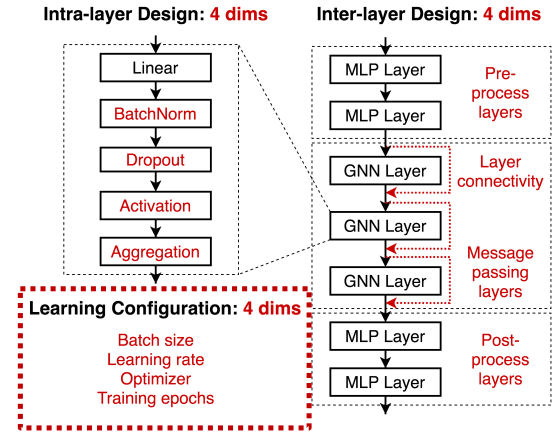
经验总结:
课程目标 1:GNN 与传统图算法的关系
课程目标 2:理解 GNN 学习映射的过程
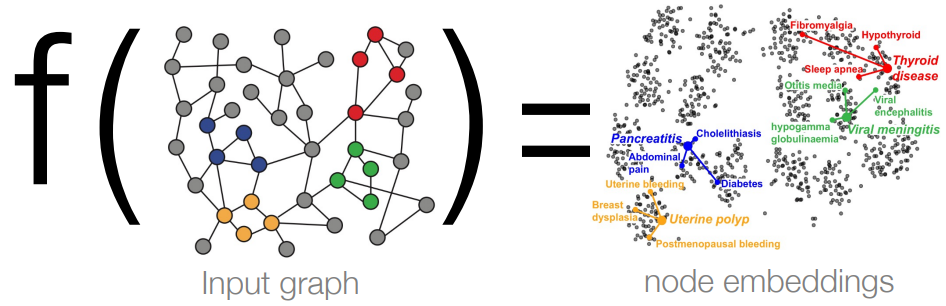
前置知识:WL 图同构检验、4 图同构网络 GIN
前置知识的概括总结:
思考:除了 1-WL,GNN 还可以轻松地模拟哪些其他任务?
任务 1:特征提取
参考文章:2024: The State of Generative AI in the Enterprise
核心观点:
Ollama 是一个支持在本地下载、管理运行大语言模型的工具
项目地址 105k ⭐
Ollama 基本操作:
ollama pull llama3.3 # 下拉模型
ollama 方案:将 config.json 文件中 num_hidden_layers 的值修改为较小的值(比如 1)
原理:隐藏层中 block 的输入输出维度是一致的,因此去除重复的 block 并不会影响模型的处理逻辑;但需要注意该方法会影响模型的性能,因此只适合模型调试阶段使用。
分层推理法:将模型根据层来进行拆分存储,推理时分批次将要处理的层导入显存
代码示例:
from accelerate import init_empty_weights
from accele