1 定积分(definite integral)
$$\int_a^bf(x)dx=F(b)-F(a)$$
- 其中$F(x)$是$f(x)$的原函数,$[a,b]$是$x$的区间范围
- 相比于不定积分有区间上下限的限制,排除了常数$c$
- 定积分表示在某个区间上函数曲线与$x$轴所围成的面积
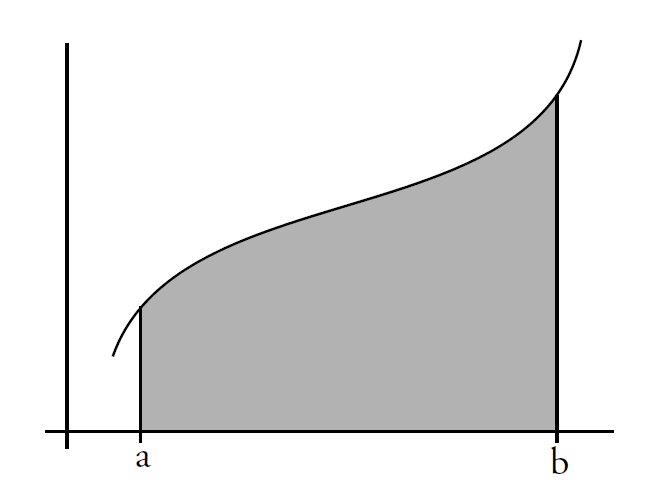
2 定积分通解-面积近似法
- 沿着$x$轴垂直切割图像,然后得到很多矩形
- 多个矩形面积的加和就是面积的近似值
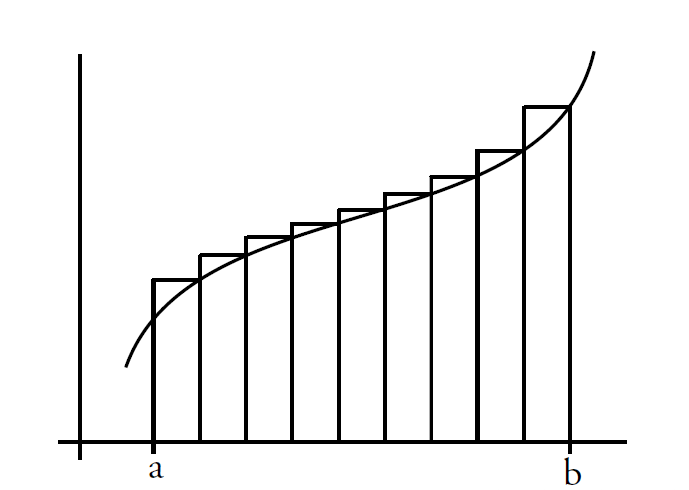
3 定积分求解
例:计算$y=x^2$从$
分类目录归档:MIT18.01单变量微积分
$$\int_a^bf(x)dx=F(b)-F(a)$$


例:计算$y=x^2$从$
例: $$(\frac{d}{dx}+x)y=0$$
具体详见: #待补充
求解上方例题
莱布尼兹的导数记法:$f'(x)=\frac{dy}{dx}$
$y$的微分就是$dy=f'(x)dx$
如果$G'(x)=g(x)$,则$G(x)$就是$g(x)$的原函数,也就是不定积分 $$G(x)=\int g(x)dx$$
例:固定绳子两端于点$(0,0)$和点$(a,b)$,并在绳子内任意位置悬挂重物,得到重物的坐标$(x,y)$,求$y$的最小值
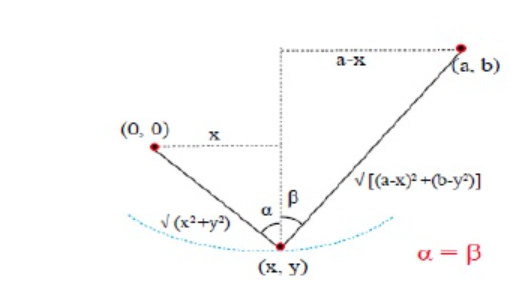
求解过程
$$\frac{1}{2}\frac{2x+2yy'}{\sqrt{x^2+y^2}}+\frac{1}{2}\frac{-2(a-x)-2(b-
复习:分析函数极值点关键是找到驻点、边界点和不连续点
例:1根绳,截2段,分别围成正方形,求总面积最大值 $$S=(\frac{x}{4})^2+(\frac{1-x}{4})^2$$
求解过程
- 令$S'=0$,可得$x=\frac{1}{2}$
- 此时$S(x=\frac{1}{2})=\frac{1}{32}$,是最小值
- 此函数的最大值为边界值,即$x=0^+or1^-$的时候最大
- 此时$S=\frac{1}{16}$,
$$\lim_{k \to \infty}a_k=\lim_{k \to \infty}(1+\frac{1}{k})^k=e$$
利用线性近似进行更简单的证明
- $ln(a_k)=k\times ln(1+\frac{1}{k})\approx k\times \frac{1}{k}=1$
二阶近似的性质
- $ln(a_k)=k\times ln(1+\frac{1}{k})\approx k\times (\frac{1}{k}-\frac{1}{2k^2})=1-\frac{1}{2k}$
- $
$$f(x) \approx f(x_0)+f'(x_0)(x-x_0)$$
以$x_0=0$且$x\approx 0$为前提,几种常见的函数线性近似:
- $sin(x) \approx x$
- $cos(x) \approx 1$
- $e^x \approx 1+x$
- $lm(1+x) \approx x$
- $(1+x)^r \a
$$\frac{d}{dr}x^r=rx^{r-1}$$ 其中$r \in$实数
快速证明 $$\frac{d}{dr}x^r=\frac{d}{dr}e^{ln(x^r)}=e^{ln(x^r)}\times r \times \frac{1}{x}=rx^{r-1}$$
股票指数,以FTSE100为例
- FTSE100全称为伦敦金融时报100指数,简称英国富时100指数
- 欧洲三大股票指数包括:30工业股、FT-100、综合