分类目录归档:机器学习
1 GNN 的架构设计
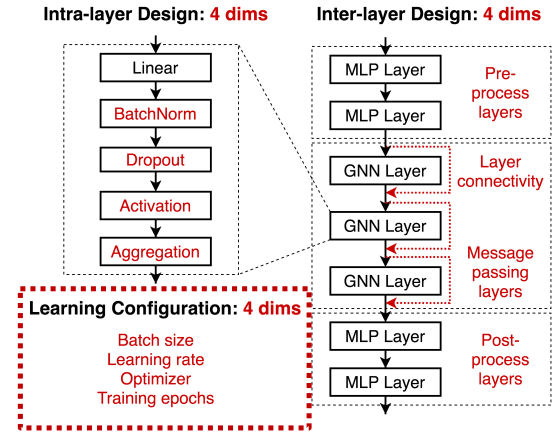
- 层内(Intra-layer)设计:核心过程信息的转换和聚合
- 层间(Inter-layer)设计:预处理层主要是对节点特征的编码,后处理层主要是对节点嵌入的推理和转换;跳过连接(skip-connection)有助于改善深度 GNN 的性能
- 学习配置(Learning configuration)对性能影响很大,还容易被忽视
经验总结:
- GNN 的可能设计结构非常多,因此设计空间的研究很重要
- GNN 很难优化,也经常容易欠拟合;训练的 epochs 越多越好
- Su
课程目标 1:GNN 与传统图算法的关系
课程目标 2:理解 GNN 学习映射的过程
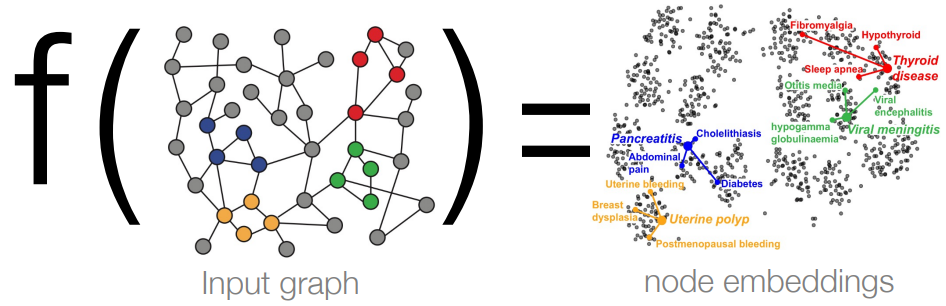
1 GNN 与经典任务
前置知识:WL 图同构检验、4 图同构网络 GIN
前置知识的概括总结:
- GIN 是 1-WL 算法的“神经版本”,二者的表现力相似
- 只不过 GIN 用可学习的 MLP 替换了 1-WL 的 HASH 函数
- 未经训练的 GNN(随机 MLP = 随机哈希)接近 1-WL 算法
思考:除了 1-WL,GNN 还可以轻松地模拟哪些其他任务?
任务 1:特征提取
- 输入:一堆包含颜色、位置描述的物体
- 输出
前置知识:因果推断入门
1 因果关系介绍
因果 DAG(有向无环图):使用图来表示因果关系
用于决策干预的链路预测任务(比如搜索或推荐)往往是存在因果关系的
因果关系在决策中的示例:
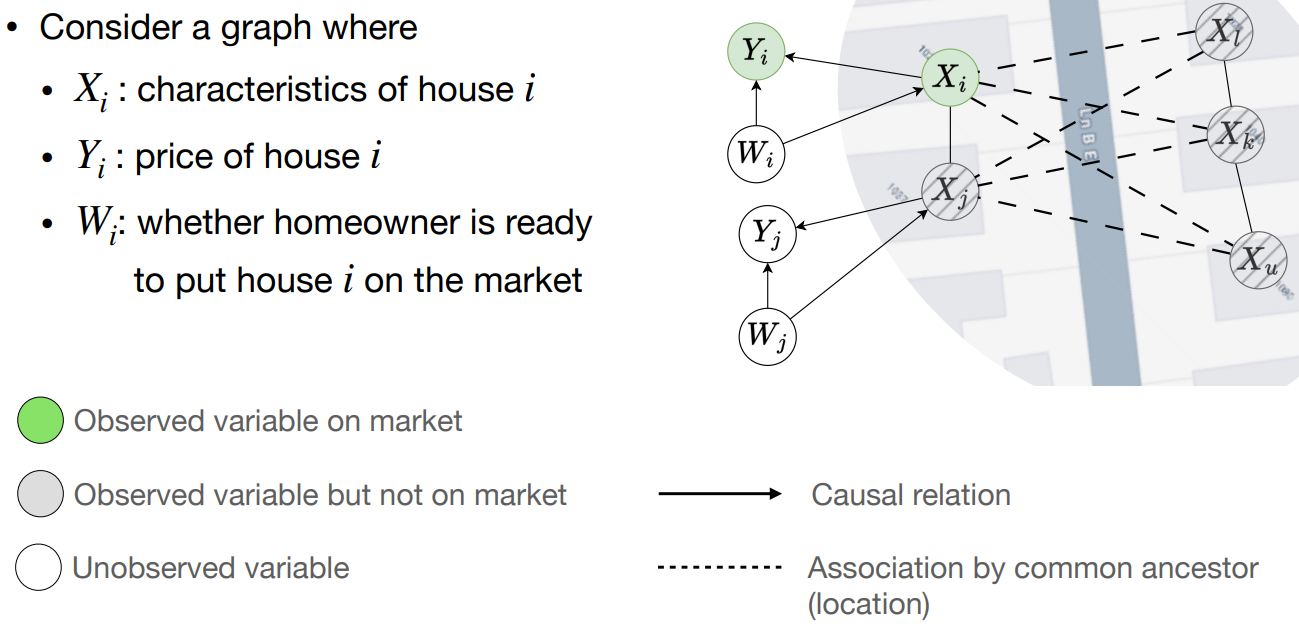
- 上图中,$X_i$ 表示第 $i$ 个房子的特征,$Y_i$ 表示第 $i$ 个房子的价格,$W_i$ 表示房主是否准备出售房子;实线表示因果关系,虚线表示由父节点决定的相关性
- 一般情况下,模型可以根据市场上的待售房屋的信息和报价,来预估个人的房屋价格;但实际应用时,房主的出售行为 $W_i$ 是房屋属性 $X_i$ 和价格 $Y
由于本小节为论文研讨课,因此本文将以论文阅读笔记的形式展开
前置知识:了解基本的共形预测 Conformal Prediction 概念与评价方法(覆盖率)
《Uncertainty Quantification over Graph with Conformalized Graph Neural Networks》
摘要:
- 本文提出了一种共形 GNN(conformalized GNN,简称 CF-GNN),将共形预测扩展到图模型以估计模型预测的不确定性。预定义覆盖率(比如 90%)后,CF-G
由于本小节为论文研讨课,因此本文将以论文阅读笔记的形式展开
《PRODIGY: Enabling In-context Learning Over Graphs》
摘要:
- 本文提出了一种名为 PRODIGY(Pretraining Over Diverse In-Context Graph System)的预训练框架,该框架借鉴了大模型的训练思路,先通过图提示(Graph Prompt)来表示图的上下文学习任务,再使用名为邻居匹配(neighbor mat
本小节目标:将 Transformers 的能力引入图神经网络
1 从 Transformers 到 GNN
前置知识:Transformer 基础、第三方资料-图解 Transformer
多头自注意力机制:
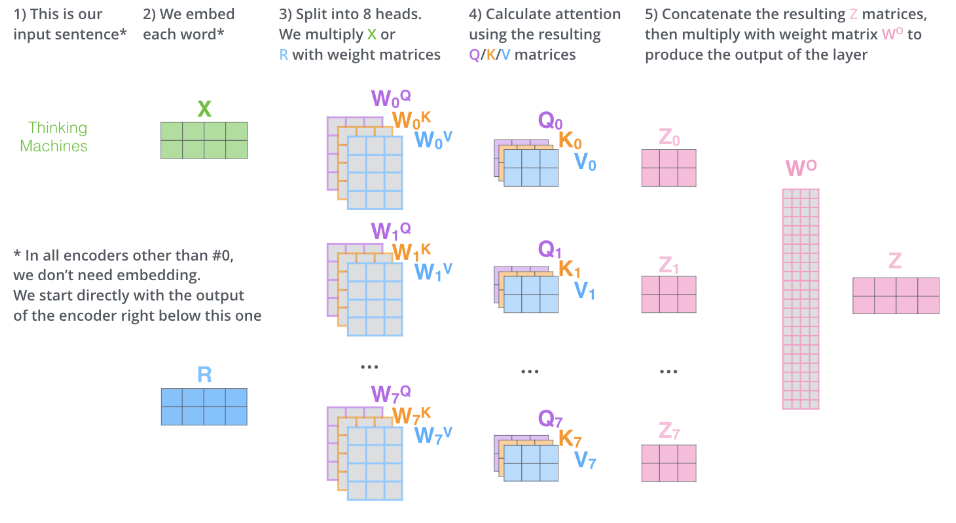
对比 Transformer 和 RNN:
- 相似点:输入一系列向量(无特定顺序),并输出一系列嵌入
- 不同点:GNN 使用消息传递,Transformer 使用自注意力机制
对比消息传递和自注意力机制:
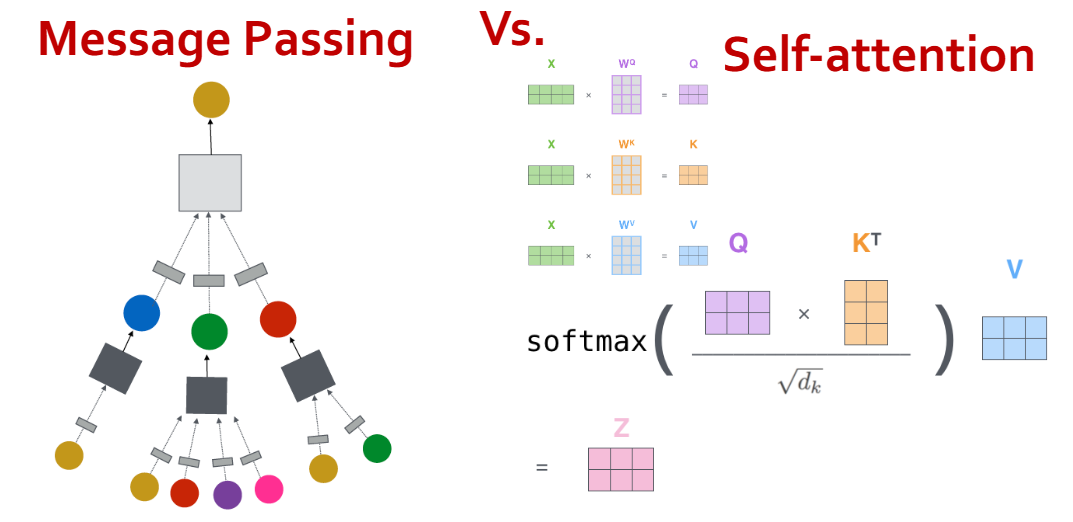
- 自注意力是消息传递的一个特例,是一种在全连接图上的消息传递
- 给定一个图
1 大型图应用与难点
当前的大型图应用场景:
- 推荐系统(亚马逊、Youtube、Pinterest 等):用户规模在 100M~1B,产品/视频规模在 10M~1B,任务包括商品推荐或用户分类
- 社交网络(Facebook、X、Instagram 等):用户规模在 300M~3B,任务包括好友推荐或用户属性预测
- 学术网络(微软学术图谱):作者或论文规模在 120M,任务包括论文分类、合作作者推荐、论文引用推荐
- 知识图谱(Wikidata、Freeb
前置知识:CS224W 图机器学习04:GNN 深入理解、CS224W 图机器学习05:GNN 的训练与预测、 CS224W 图机器学习06:GNN 的理论理解
本节主题:如何使得 GNN 的嵌入更具表示力?
1 图神经网络的局限性
一个"完美"的 GNN 应该具备什么特征?
- 能在邻域结构(无论跃点如何)和节点嵌入之间构建一个单射函数
- 如果两个节点具有相同的邻域结构,则它们必须具有相同的嵌入
- 如果两个节点具有不同的邻域结构,则它们必须具有不同的嵌入
问题 1:
1 深度图生成模型基础
图生成的应用:药物发现、材料设计、社交网络建模
图生成的意义:理解图的表达、预测图的演变、实现图的模拟、检测图的异常
图生成的发展:(1)根据现实世界构建图(2)传统图生成(3)深度图生成
之前学习的图编码是一个 encoding 的过程,而图生成是一个 decoding 的过程
图生成的目标:给定来自 $p_{data}(G)$ 的图采样,构建模型 $p_{model}(G)$ 学习图的分布

图生成的的过程
- 基于最大似然估计,让