2.面试需要的基础知识

1 面试官谈基础知识
2 编程语言
- 2.1 面试题1：赋值运算符函数
- 2.2 面试题2：实现Singleton模式
3 数据结构

1 面试官谈基础知识

擅长的编程语言的特性和深入理解
设计模型、UML图
内存管理、并发、性能、安全
基础数学（概率）
问题分析和推理能力
算法、复杂度

2 编程语言

C++、C#、Java、Python

本小节以C++和C#为例，进行了常见面试题的说明和思路介绍，还提供了进阶学习的相关书籍推荐，由于本人C++只学过一点，因此简单记录相关知识点

C++中的空类型实例，不包含任何信息，但由于已声明类型，在内存中占用1字节的空间
空类型实例添加构造函数和析构函数后，函数地址与类型有关，与实例无关，因此内存占用不变，还是1字节
类型添加虚函数后，会生成虚函数表，实例需要记录指向虚函数表的指针，在32位机器上，一个指针占4字节的空间，在64位机器上，一个指针占8字节的空间

构造函数析构函数虚函数虚函数表 #待补充

C++进阶阅读推荐

2.1 面试题1：赋值运算符函数

C++题目，解题思路暂略

可参考：一文说尽C++赋值运算符重载函数(operator) 《剑指Offer》面试题1：赋值运算符函数

2.2 面试题2：实现Singleton模式

C#题目，解题思路暂略

2.2.1 Python实现方法1：使用模块

Python 的模块就是天然的单例模式，因为模块在第一次导入时，会生成 .pyc 文件，当第二次导入时，就会直接加载 .pyc 文件，而不会再次执行模块代码。因此，我们只需把相关的函数和数据定义在一个模块中，就可以获得一个单例对象了。

# mysingleton.py

class Singleton(object):
    def foo(self):
        pass
singleton = Singleton()

from mysingleton import singleton

此方法在[[4_book/Python编程/编写高质量代码改善 Python 程序的 91 个建议/5.《Python高质量代码的91个建议》设计模式#建议 50：利用模块实现单例模式]]中有提及

2.2.2 Python实现方法2：借助装饰器decorator

def Singleton(cls):
    _instance = {}
    def _singleton(*args, **kargs):
        if cls not in _instance:
            _instance[cls] = cls(*args, **kargs)
        return _instance[cls]
    return _singleton

@Singleton
class A(object):
    a = 1
    def __init__(self, x=0):
        self.x = x

a1 = A(2)
a2 = A(3)

2.2.3 Python实现方法3：基于`new`方法

实例化一个对象时，是先执行了类的__new__方法实例化对象；然后再执行类的__init__方法，对这个对象进行初始化。因此可以在__new__方法中添加单例限制。

同时也要注意为了保证线程安全需要在内部加入锁

import threading
class Singleton(object):
    _instance_lock = threading.Lock()

    def __init__(self):
        pass

    def __new__(cls, *args, **kwargs):
        if not hasattr(Singleton, "_instance"):
            with Singleton._instance_lock:
                if not hasattr(Singleton, "_instance"):
                    Singleton._instance = object.__new__(cls)  
        return Singleton._instance

obj1 = Singleton()
obj2 = Singleton()
print(obj1,obj2)

def task(arg):
    obj = Singleton()
    print(obj)

# 验证单例模式是否满足线程安全
for i in range(10):
    t = threading.Thread(target=task,args=[i,])
    t.start()

2.2.4 Python实现方法4：基于`metaclass`

类由type创建，创建类时，type的__init__方法自动执行，类() 执行type的__call__方法
执行type的 __call__ 方法时，将调用类（是type的对象）的 __new__方法，用于创建对象，然后调用类（是type的对象）的 __init__方法，用于对象的初始化。
对象由类创建，创建对象时，类的__init__方法自动执行，对象()执行类的__call__方法

import threading

class SingletonType(type):
    _instance_lock = threading.Lock()
    def __call__(cls, *args, **kwargs):
        if not hasattr(cls, "_instance"):
            with SingletonType._instance_lock:
                if not hasattr(cls, "_instance"):
                    cls._instance = super(SingletonType,cls).__call__(*args, **kwargs)
        return cls._instance

class Foo(metaclass=SingletonType):
    def __init__(self,name):
        self.name = name

obj1 = Foo('name')
obj2 = Foo('name')
print(obj1,obj2)

本小节内容主要参考自Python中的单例模式的几种实现方式的及优化

3 数据结构

3.1 数组

占用连续内存空间，顺序存储，读写效率为O(1)
通过将下标设为哈希表的键值（key），实现O(1)的查找效率
内存是预分配的，空间利用率低，可通过动态数组减少浪费

3.1.1 面试题3：数组中重复的数字

在一个长度为n的数组里的所有数字都在0到n-1的范围内。数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。

示例

输入：[2, 3, 1, 0, 2, 5, 3]

输出：2 或 3

思路

O(nlogn)复杂度的排序，然后遍历排序后的数组

建立哈希表O(n)，哈希表中存在表面此数字是重复的

由于数字范围在0~n-1，所以可以借助n维数组自带的索引

测试用例

数字范围在0到n-1的n维数组

无重复数字的数组

无效用例（空数组、数字范围不在0到n-1等）

3.1.1.1 Python实现方法1：哈希表/Set

class Solution:
    def findRepeatNumber(self, nums: [int]) -> int:
        dic = set()
        for num in nums:
            if num in dic: return num
            dic.add(num)
        return -1

复杂度分析：

时间复杂度 O(N) ：遍历数组使用 O(N) ，HashSet 添加与查找元素皆为 O(1) 。空间复杂度 O(N) ： HashSet 占用 O(N) 大小的额外空间。

3.1.1.2 Python实现方法2：原地交换

class Solution:
    def findRepeatNumber(self, nums: [int]) -> int:
        i = 0
        while i < len(nums):
            if nums[i] == i:
                i += 1
                continue
            if nums[nums[i]] == nums[i]: return nums[i]
            nums[nums[i]], nums[i] = nums[i], nums[nums[i]]
        return -1

复杂度分析：

时间复杂度 O(N)：遍历数组使用 O(N)，每轮遍历的判断和交换操作使用 O(1) 。空间复杂度 O(1) ：使用常数复杂度的额外空间。

Python实现思路的参考链接

3.1.2 面试题4：二维数组中的查找

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例

现有矩阵 matrix 如下：
[

[1, 4, 7, 11, 15], [2, 5, 8, 12, 19], [3, 6, 9, 16, 22], [10, 13, 14, 17, 24], [18, 21, 23, 26, 30] ]

- 给定 target = 5，返回 true。
- 给定 target = 20，返回 false。

思路

暴力求解，复杂度为O(mn)，不可取

根据“上下递增、左右递增”的特性，进行线性搜索

测试用例

二维数组包含查找的数字

二维数组不包含查找的数字

无效用例（空数组，非数字等）

3.1.2.1 Python实现方法：线性搜索

class Solution:
    def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
        i, j = len(matrix) - 1, 0
        while i >= 0 and j < len(matrix[0]):
            if matrix[i][j] > target: i -= 1
            elif matrix[i][j] < target: j += 1
            else: return True
        return False

复杂度分析：

时间复杂度 O(M+N) ：其中，N 和 M 分别为矩阵行数和列数，此算法最多循环 M+N 次。空间复杂度 O(1) : i, j 指针使用常数大小额外空间。

Python实现思路的参考链接

3.2 字符串

C++/C#中字符串都是以\0结尾
为了节省内存，C++/C#中常量字符串索引都指向相同的内存空间
Java或Python中字符串都是不可变对象，而C++中是可变的，所以字符串能原地修改

3.2.1 面试题5：替换空格

请实现一个函数，把字符串 s 中的每个空格替换成"%20"。

示例

输入：s = "We are happy."

输出："We%20are%20happy."

思路

遍历查看，依次赋值给新字符串，并在遇到空格时替换

遍历查看，在不新建字符串的情况下实现原地修改（仅C++支持）

测试用例

输入的字符串包含空格

输入的字符串不包含空格

特殊输入测试（空字符串、只有一个空格、连续多个空格等等）

3.2.1.1 Python实现方法：遍历添加

class Solution:
    def replaceSpace(self, s: str) -> str:
        res = []
        for c in s:
            if c == ' ': res.append("%20")
            else: res.append(c)
        return "".join(res)

复杂度分析：

时间复杂度 O(N) ：遍历使用 O(N) ，每轮添加（修改）字符操作使用 O(1) 。空间复杂度 O(N) ： Python 新建的 list 使用了线性大小的额外空间。

Python实现思路的参考链接

3.3 链表

链表结构是由指针把若干个节点连接成链状结构
链表是一种动态数据结构，新增节点伴随着内存的分配，所以内存空间效率高
由于链表在内存中不是连续的，所以每次查询只能从头开始，时间效率为O(n)

3.3.1 面试题6：从尾到头打印链表

输入一个链表的头节点，从尾到头反过来返回每个节点的值（用数组返回）。

示例

输入：head = [1,3,2]

输出：[2,3,1]

思路

遍历链表，然后利用栈"后进先出"的特性返回值

递归本质也是一种栈结构，所以可以用递归法输出下一个节点

测试用例

功能测试（单节点链表、多节点链表）

特殊输入测试（链表头节点指针为空）

3.3.1.1 Python实现方法1：辅助栈法

class Solution:
    def reversePrint(self, head: ListNode) -> List[int]:
        stack = []
        while head:
            stack.append(head.val)
            head = head.next
        return stack[::-1]

复杂度分析：

时间复杂度 O(N)：入栈和出栈共使用 O(N) 时间。空间复杂度 O(N)：辅助栈 stack 和数组 res 共使用 O(N) 的额外空间。

3.3.1.2 Python实现方法2：递归法

class Solution:
    def reversePrint(self, head: ListNode) -> List[int]:
        return self.reversePrint(head.next) + [head.val] if head else []

复杂度分析：

时间复杂度 O(N)：遍历链表，递归 N 次。空间复杂度 O(N)：系统递归需要使用 O(N) 的栈空间。

Python实现思路的参考链接

3.4 树

除根节点外的节点都只有一个父节点
除叶节点外的节点都有一个或多个的子节点
父节点和子节点之间用指针链接

几种常见的树结构

二叉树：子节点的度不超过2的树

满二叉树：除了叶子结点，每个结点的度都为 2的二叉树

完全二叉树：除去最后一层节点为满二叉树，且最后一层的结点连续集中在左边

最大堆/最小堆：根节点为最大值/最小值的完全二叉树

二叉查找树\二叉排序树\二叉搜索树：一种用于查找的二叉树

平衡二叉树之AVL树\红黑树：保持左右两个子树的高度差的绝对值不超过1

B树：一种用于查找的平衡树，但不是二叉树

B+树：B树的变体，也是一种多路搜索树

树结构部分参考自数据结构中各种树

树的遍历

前序遍历：先根、再左、最后右

中序遍历：先左、再根、最后右

后序遍历：先左、再右、最后根

记忆技巧：先左后右，根看方法名称，实现分递归和循环两种方法

遍历分为宽度优先遍历和广度优先遍历两种

3.4.1 面试题7：重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例

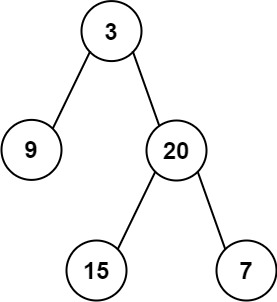
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

Output: [3,9,20,null,null,15,7]

思路

根据前序遍历可以确定根节点为3

根据中序遍历可以确定根节点的两个子树遍历结果

左子树中序遍历结果为[9]；右子树中序遍历结果为[15,20,7]

而由前序遍历可知右子树前序遍历结果为[20,15,7]，最后递归重复以上过程

测试用例

普通二叉树（完全、不完全）

特殊二叉树（单节点、无左子节点、无右子节点）

特殊输入测试（根节点指针为空；前序遍历和中序遍历不匹配）

3.4.1.1 Python实现方法：分治法

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        def recur(root, left, right):
            if left > right: return                               # 递归终止
            node = TreeNode(preorder[root])                       # 建立根节点
            i = dic[preorder[root]]                               # 划分根节点、左子树、右子树
            node.left = recur(root + 1, left, i - 1)              # 开启左子树递归
            node.right = recur(i - left + root + 1, i + 1, right) # 开启右子树递归
            return node                                           # 回溯返回根节点

        dic, preorder = {}, preorder
        for i in range(len(inorder)):
            dic[inorder[i]] = i
        return recur(0, 0, len(inorder) - 1)

复杂度分析：

时间复杂度 O(N) ：其中 N 为树的节点数量。初始化 HashMap 需遍历 inorder ，占用 O(N) 。递归共建立 N 个节点，每层递归中的节点建立、搜索操作占用 O(1) ，因此使用 O(N) 时间。

空间复杂度 O(N) ： HashMap 使用 O(N) 额外空间；最差情况下（输入二叉树为链表时），递归深度达到 N ，占用 O(N) 的栈帧空间；因此总共使用 O(N) 空间。

Python实现思路的参考链接

3.4.2 面试题8：二叉树的下一个节点

给定一个二叉树和其中的一个结点，找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。

#单例模式 #哈希 #链表 #二叉树

个人笔记

Digital Garden | 王半仙

1 面试官谈基础知识

2 编程语言

2.1 面试题1：赋值运算符函数

2.2 面试题2：实现Singleton模式

2.2.1 Python实现方法1：使用模块

2.2.2 Python实现方法2：借助装饰器decorator

2.2.3 Python实现方法3：基于`new`方法

2.2.4 Python实现方法4：基于`metaclass`

3 数据结构

3.1 数组

3.1.1 面试题3：数组中重复的数字

3.1.1.1 Python实现方法1：哈希表/Set

3.1.1.2 Python实现方法2：原地交换

3.1.2 面试题4：二维数组中的查找

3.1.2.1 Python实现方法：线性搜索

3.2 字符串

3.2.1 面试题5：替换空格

3.2.1.1 Python实现方法：遍历添加

3.3 链表

3.3.1 面试题6：从尾到头打印链表

3.3.1.1 Python实现方法1：辅助栈法

3.3.1.2 Python实现方法2：递归法

3.4 树

3.4.1 面试题7：重建二叉树

3.4.1.1 Python实现方法：分治法

3.4.2 面试题8：二叉树的下一个节点

1 面试官谈基础知识

2 编程语言

2.1 面试题1：赋值运算符函数

2.2 面试题2：实现Singleton模式

2.2.1 Python实现方法1：使用模块

2.2.2 Python实现方法2：借助装饰器decorator

2.2.3 Python实现方法3：基于__new__方法

2.2.4 Python实现方法4：基于metaclass

3 数据结构

3.1 数组

3.1.1 面试题3：数组中重复的数字

3.1.1.1 Python实现方法1：哈希表/Set

3.1.1.2 Python实现方法2：原地交换

3.1.2 面试题4：二维数组中的查找

3.1.2.1 Python实现方法：线性搜索

3.2 字符串

3.2.1 面试题5：替换空格

3.2.1.1 Python实现方法：遍历添加

3.3 链表

3.3.1 面试题6：从尾到头打印链表

3.3.1.1 Python实现方法1：辅助栈法

3.3.1.2 Python实现方法2：递归法

3.4 树

3.4.1 面试题7：重建二叉树

3.4.1.1 Python实现方法：分治法

3.4.2 面试题8：二叉树的下一个节点

2.2.3 Python实现方法3：基于`new`方法

2.2.4 Python实现方法4：基于`metaclass`