中文标题: 通过不确定性量化和主动感知进行早期脓毒症预测
英文标题:SepsisLab: Early Sepsis Prediction with Uncertainty Quantification and Active Sensing
发布平台:SIGKDD
发布日期:2024-08-01
引用量(非实时):7
DOI:10.1145/3637528.3671586
作者:Changchang Yin, Pin-Yu Chen, Bingsheng Yao, Dakuo Wang, Jeffrey Caterino, Ping Zhang
关键字: #SepsisLab
文章类型:journalArticle
品读时间:2025-05-13 10:46
1 文章萃取
1.1 核心观点
本文首先针对现实临床场景下的数据普遍缺失情况,将信息缺失导致的预测不确定性定义为预测输出的方差,然后引入不确定性传播方法来量化传播的不确定性,并借助主动感知的方式给出能最大程度减少预测不确定性的缺失变量推荐。
本文构建了缺失值插补模型与脓毒症预测模型,首先了入院初期脓毒症风险的实时预测与不确定性量化,同时本文算法效果在三个数据集中得到了有效验证;最后本文将所有功能进行汇总,提出了一种实用且落地的 SepsisLab 系统用于脓毒症的风险预测和患者检验项目的推荐。
1.2 综合评价
- 基本模型框架较为简单,存在继续改进和完善的空间
- 引入对抗训练来确定局部线性,方便不确定性的传播
- 代码开源,功能集成到 SepsisLab 系统,实用价值高
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
前置知识:脓毒症 Sepsis
模型框架总览:
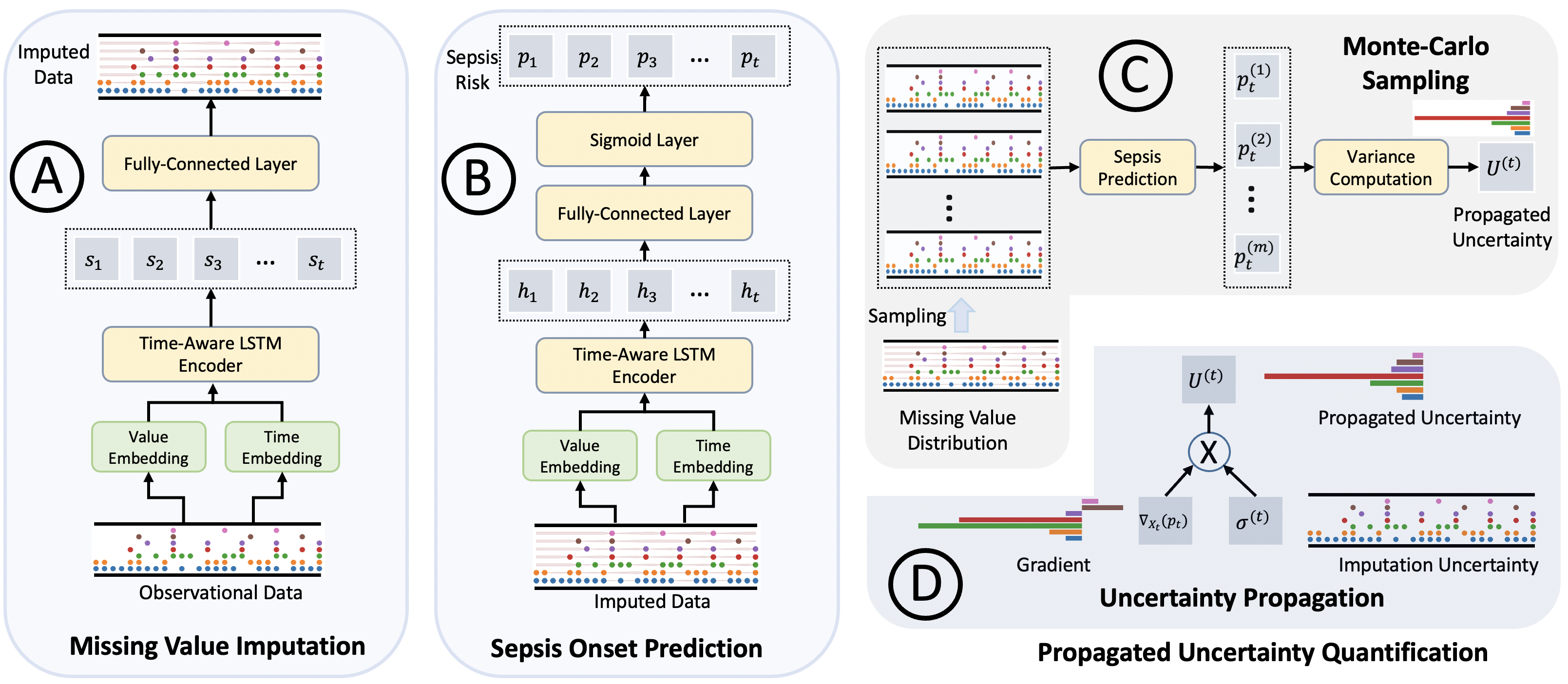
- (A)缺失值插补模型:输入为可观测变量及其时间戳,输出为缺失值的分布
- (B)脓毒症预测模型:基于插补后的数据,预测脓毒症的风险及其不确定性
- (C)基于蒙特卡洛采样的不确定性量化方法,用于量化插补值的不确定性
- (D)模型通过插补值梯度值及其不确定性的相乘,来估计传播的不确定性
2.1 缺失值插补模型
缺失值插补模型:
- 假设缺失值服从高斯分布,模型需要估计缺失变量的分布(均值和协方差)
- 嵌入层:第 $i$ 个样本集合的嵌入表示 $e_{i}=w_{e}[Z_{i};e^t_{i}]+b_{e}$,其中 $Z_{i}$ 为包含缺失的观测特征,$e^t_{i}$ 为使用正弦和余弦函数进行处理的时间位置编码,$w$ 和 $b$ 为可训练参数
- 编码层:基于时间感知的 LSTM 编码,给定嵌入向量来建模患者的状态:
$$s_{1},s_{2},...,s_{n}=LSTM(e_{1},e_{2},...,e_{n}) $$
- 分布估计:使用全连接层生成缺失变量的均值 $\mu$ 和方差 $\sigma$
$$ \mu_{i}=w_{\mu}s_{i}+b_{\mu}, \quad \sigma_{i}=ReLU(w_{\sigma}s_{i}+b_{\sigma}) $$
- 预训练阶段:针对均值预测使用均方误差损失函数,其中 $M$ 表示掩码矩阵,当第 $i$ 个样本的第 $j$ 个可观察变量被掩盖时,设置 $M_{i,j}=1$
$$ \mathcal{L}_{imp}(Z,M,\mu)=\sum_{i=1}^{n}\sum_{j=1}^{k}M_{i,j}(\mu_{i,j}-Z_{i,j})^{2} $$
- 微调阶段:针对标准差预测使用对数似然损失
$$\mathcal{L}_{\sigma}(Z,M,\mu,\sigma)=\sum_{i=1}^{n}\sum_{j=1}^{k}M_{i,j}[\frac{\left(\mu_{i,j}-Z_{i,j}\right)^{2}}{2\sigma_{i,j}^{2}}+\frac{\sigma_{i,j}^{2}}{2}]$$
2.2 脓毒症预测模型
预测机制:每小时触发一次,预测患者是否会在 4 小时内患上脓毒症
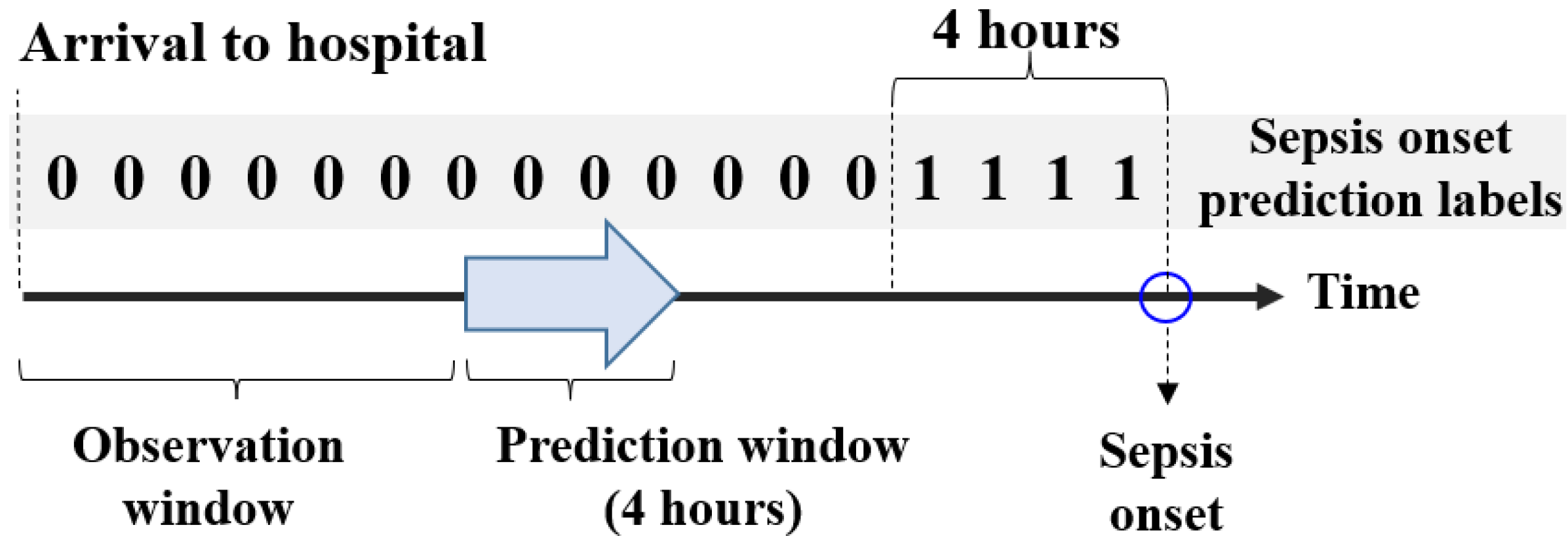
脓毒症预测模型:
- 使用和缺失插补模型相同的嵌入层和 LSTM 编码层
- 后接一个全连接层和 Sigmoid 层,用于脓毒症的风险预测
- 模型通过最小化二元交叉熵损失进行训练
2.3 不确定性量化与主动感知
不确定性的两个主要来源:
- 模型参数的不确定性,在测试阶段使用 dropout,并多次运行推理来量化此类不确定性
- 缺失值带来的不确定性,插补方法的准确性会直接影响预测败血症风险的性能
遵循现有研究,本文将预测结果的不确定性定义为模型输出结果的方差 $U$
$$ \begin{aligned} & U=\int_{w}\int_{x}\left(f_{w}(x)-\mu_{y}\right)^{2}\rho(x)dx\rho(w)dw=U_{x}+U_{w} \\ & \mathrm{where} \ U_{x}=\int_{w}\int_{x}(f_{w}(x)-\mu_{y_{w}})^{2}\rho(x)dx\rho(w)dw, \\ & U_{w}=\int_{w}(\mu_{y_{w}}-\mu_{y})^{2}\rho(w)dw, \\ & \mu_{y_{w}}=\int_{x}f_{w}(x)\rho(x)dx, \\ & \mu_{y}=\int_{w}\int_{x}f_{w}(x)\rho(x)\rho(w)dxdw, \end{aligned} $$
- 其中 $U_{x}$ 表示缺失值带来的不确定性,$U_{w}$ 表示模型参数的不确定性
- 本文假设输入变量 $x$ 和模型参数 $w$ 分别服从高斯分布 $N(\mu_{x},\sigma_{x})$ 和 $N(\mu_{w},\sigma_{w})$
- 当模型参数 $w$ 固定时,估计的不确定性为 $U_{x}^{(w)}=\int_{x}(f_{w}(x)-\mu_{y_{w}})^2\rho(x)dx$
- 因此可使用蒙特卡洛 dropout 采样模型参数,并用 $U_{x}^{(w)}$ 的均值来表示 $U_{x}$
不确定性的传播:
- 当预测模型为线性函数时(比如 $f_{w}(x)=\Sigma_{j} w_{j}x_{j}$),很容易计算传播的不确定性
$$ U_{x}^{(w)}=\sum_{i}w_{i}^{2}\sigma_{x_{i}}^{2}+\sum_{i}\sum_{j\neq i}w_{i}w_{j}\rho_{ij}\sigma_{x_{i}}\sigma_{x_{j}} $$
- 当预测模型为非线性函数时,可考虑使用泰勒展开作为近似函数
$$ \tilde{f}_{w}(x+\delta)=f_{w}(x)+\delta^{T}\nabla_{x}f_{w}(x) $$
由于使用了截断级数展开,非线性函数的传播不确定性估计存在偏差;可通过局部线性对抗训练,确保 $f_{w}$ 在 $u_{x}$ 附近的足够小的邻域内是局部线性的,这样传播的不确定性仍然是准确的
局部线性对抗训练:
- 对于非线性预测函数 $f_{w}$,定义函数 $g$ 来描述 $f_{w}$ 与近似函数 $\tilde{f}_{w}$ 在邻域内的误差绝对值
$$ g(\delta,x)=|f_w(x+\delta)-f_w(x)+\delta^T\nabla_xf_w(x)| $$
- 随机采样一批患者数据,包括 $x,\sigma_{x},y$,然后初始化随机扰动 $\delta \sim N(0,\sigma_{x})$
- 定义对抗训练的损失函数:$\mathcal{L}{adv}=\min{w}\max_{\delta}g(\delta,\mu_{x}),\mathrm{where}-2\sigma_{x}<\delta<2\sigma_{x}$
- 脓毒症预测模型的损失函数更新:$\mathcal{L}=\alpha\mathcal{L}{cls}+(1-\alpha )\mathcal{L}{adv}$
- 最终定义不确定性的量化指标 $\gamma (\sigma, x)$
$$ \gamma(\sigma,x)=\max_{-2\sigma\leq\delta\leq2\sigma}|f_{w}(x+\delta)-f_{w}(x)-\delta^{T}\nabla_{x}f_{w}(x)| $$
因为假设变量缺失值服从高斯分布,所以 $\delta$ 位于两个标准差范围内的概率在 95%以上,即不确定估计的误差有 95%以上的概率小于 $\gamma (\sigma, x)$
主动感知:根据最大不确定性原则来筛选信息量最大且成本最小的变量
2.4 实验分析与总结
核心特征变量:心率、呼吸、体温、SpO2、收缩压、舒张压、平均血压、血糖、碳酸氢盐、白细胞、带状核细胞、C 反应蛋白、尿素氮、格拉斯哥昏迷评分、尿量、肌酐、血小板、钠、血红蛋白、氯离子、乳酸、国际标准化比值、部分促凝血酶原时间、镁、阴离子间隙、血细胞比容、凝血酶原时间
数据集:MIMIC3(开源)、AmsterdamUMCdb(开源)、OSUWMC(私有数据集)
| MIMIC | AmsterdamUMCdb | OSUWMC | |
|---|---|---|---|
| #. of patients 病人数量 | 21,686 | 6,560 | 85,181 |
| #. of male 男性数量 | 11,862 | 3,412 | 41,710 |
| #. of female 女性数量 | 9,824 | 3,148 | 43,471 |
| Age (mean ± std) 年龄(平均数±标准差) | 60.7 ± 11.6 | 62.1 ± 12.3 | 59.3 ± 16.1 |
| Missing rate 缺失率 | 65% | 68% | 75% |
| Sepsis rate 脓毒症患病率 | 32% | 35% | 29% |
结论 1:随着不确定性的增加,模型的预测性能也呈下滑趋势

结论 2:缺失值导致不确定性在入院初期占主导地位,15h 后与模型参数的不确定性持平

结论 3:随着可额外观察到的缺失变量增多,预测的脓毒症风险不确定性显著降低

- RAS 表示本文方法,RAS-L 使用线性拘束,RAS-N 未使用约束
- 通过对抗训练,RAS 比 RAS-L 实现了更好的局部线性,因此表现最佳
其他结论:
- RAS 不确定性量化的推理时间比基线方法所需时间少得多,工作更高效
- RAS 的主动感知能够通过少数的额外变量观察,实现不确定性的显著减少
2.5 SepsisLab 系统界面说明
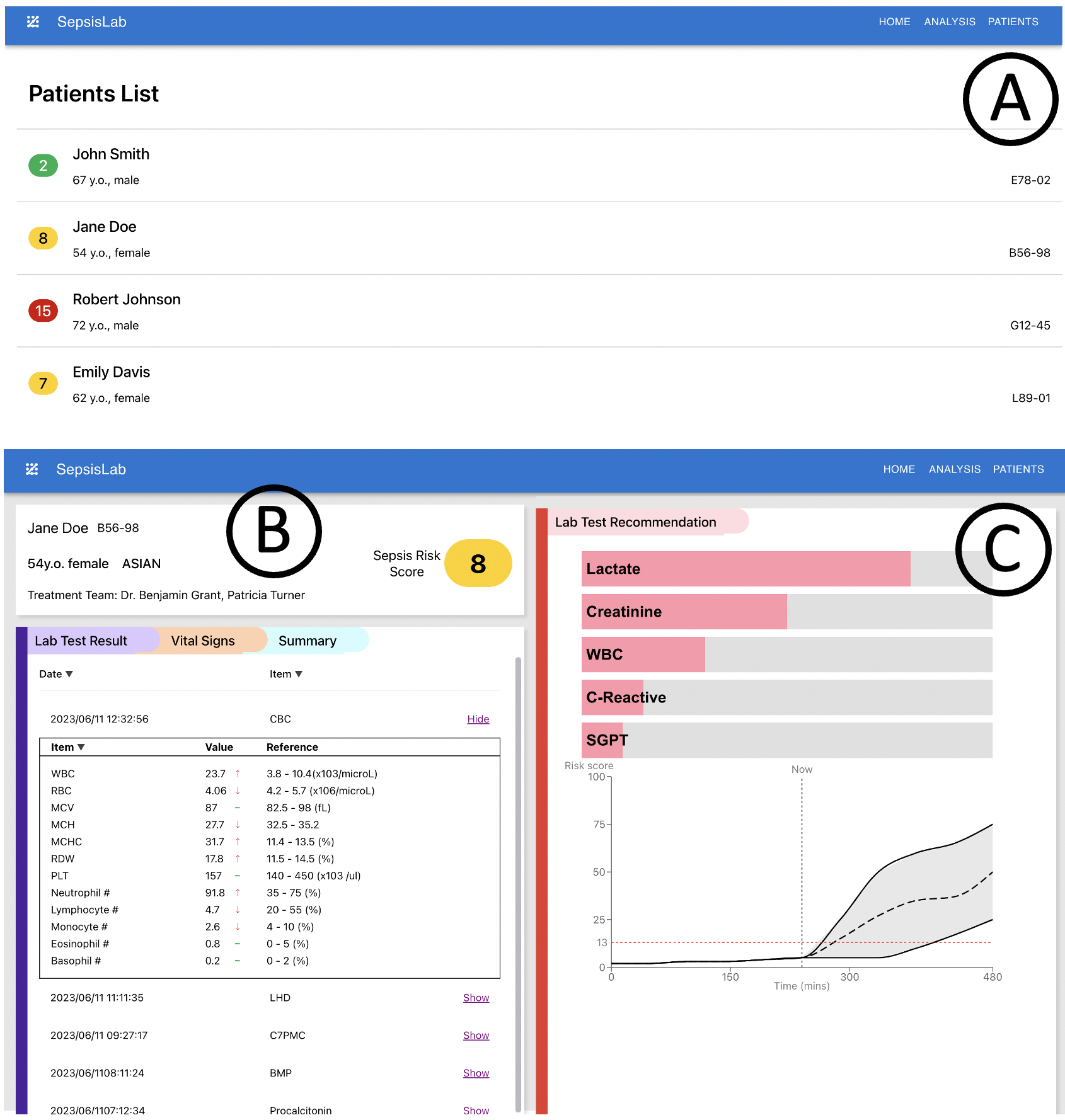
- (A)带有脓毒症风险预测分数的患者列表
- (B)患者的基本信息和患者历史数据的观察仪表板
- (C-上)主动感知的额外变量推荐,可用于检查项的推荐
- (D-上)带有不确定性量化的脓毒症风险得分的预测曲线
相关资源
- 论文在线地址
- 项目开源地址
- 本地文件地址:Preprint PDF
- 本地Zotero地址:Preprint PDF