英文标题：Heterogeneous Graph Transformer
发布平台：WWW
发布日期：2020-04-20
引用量（非实时）：1064
DOI：10.1145/3366423.3380027
作者：Ziniu Hu, Yuxiao Dong, Kuansan Wang, Yizhou Sun
关键字： #HGT #异构图 #HGSampling
文章类型：conferencePaper
品读时间：2024-05-08 17:24
1 文章萃取
1.1 核心观点
本文围绕异构图的信息传递和聚合，提出了一种异构图表示学习方法，其特点如下：（1）引入与节点和边类型相关的注意机制来处理图的异质性，同时使用更少的参数来捕捉不同类型间的关系和模式（2）提出相对时间编码 (RTE) 策略来增强 HGT 处理动态图的能力（3）设计了 HGSampling 异构子图采样算法用于小批量 GNN 训练，并增强了 HGT 处理大规模网络数据的能力
实验结果表明，与最先进的 GNN 以及专用异构图模型相比，HGT 可以将各种下游任务的性能表现提高 9-21 %，并能够自动捕获不同任务的隐式元路径的重要性
1.2 综合评价
- 将边类型和节点信息融入注意力机制中，实现对异质图的处理
- 通过异构子图采样和相对时间编码方法对 HGT 的适用性进行增强
- HGT 的模型适用性较强，可考虑探索对异构图和普通图的整合训练
1.3 主观评分：⭐⭐⭐⭐⭐
2 精读笔记
2.1 算法细节
前置知识：1 异构图的定义与理解
HGT 框架：
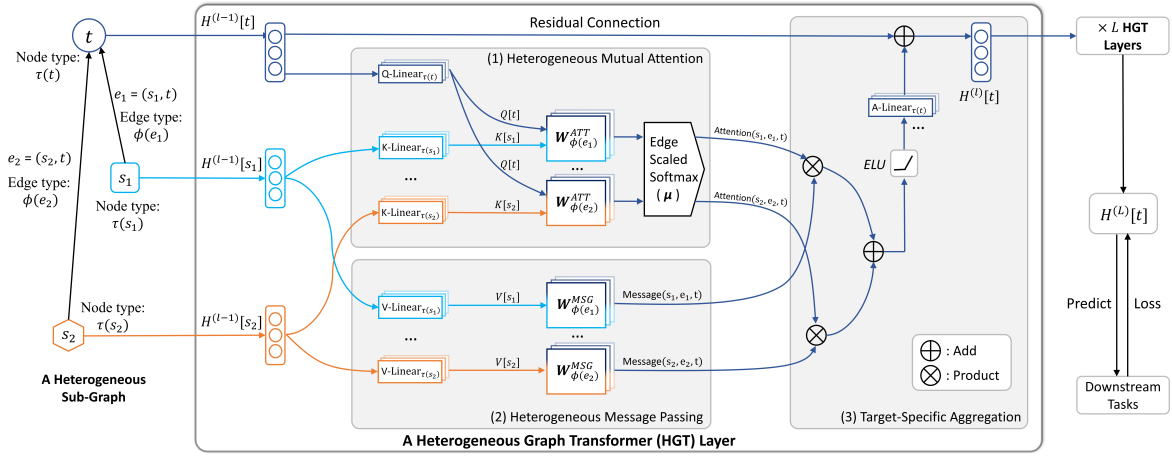
- Heterogeneous mutual attention 根据异构关系计算节点间的注意力得分
- Heterogeneous message passing 实现了异构图中节点信息的提取和传递
- Target-specific aggregation 聚合异构图中邻域信息，并用于最终的目标任务
2.1.1 异构相互注意力
给定一个目标节点 $t$ 及其所有邻居 $s\in N(t)$，其对应的边为 $e=(s,t)$；定义节点 $t$ 的类型为 $\tau(t)$，边 $e$ 的类型为 $\phi(e)$；Heterogeneous mutual attention 模块对应的计算过程如下： $$ \textbf{Attention}_{HGT}(s,e,t) = \mathop{\text{Softmax}}\limits_{\begin{array}{c}\forall s\in N(t) \\\end{array}}\Big(\underset{i\in[1,h]}{\operatorname*{|}}ATT{-}head^{i}(s,e,t)\Big) $$ $$ \begin{gathered} ATT{-}head^{i}(s,e,t) =\left(K^{i}(s) W_{\phi(s)}^{ATT}Q^{i}(t)^{T}\right)\cdot\frac{\mu_{\langle\tau(s),\phi(s),\tau(t)\rangle}}{d} \\ K^{i}(s) =\mathrm{K{-}Linear}_{\tau(s)}^{i}\biggl(H^{(l-1)}[s]\biggr) \\ Q^{i}(t) =\mathrm{Q{-}Linear}_{\tau(t)}^{i}\biggl(H^{(l-1)}[t]\biggr) \end{gathered} $$
- 自下往上看，该模块先将目标节点 $t$ 在第 $l-1$ 层的嵌入表示映射为 Query 向量 $Q^i(t)$，然后将源节点 $s$ 在第 $l-1$ 层的嵌入表示映射为 Key 向量 $K^i(s)$；其中 $i$ 表示多头注意力机制的第 $i$ 个注意力头
- 映射后的两个向量（$Q^i(t)$，$K^i(s)$）会考虑节点类型信息，即不同类型的节点对应不同的线性投影向量，该向量在上式中表示为线性映射函数： $\mathrm{K{-}Linear}$ 和 $\mathrm{Q{-}Linear}$
- $ATT{-}head$ 函数主要用于计算 $Q^i(t)$ 和 $K^i(s)$ 间的相似度/注意力向量；类似于 $\mathrm{Q{-}Linear}$ 之于节点类型，$W_{\phi(s)}^{ATT}$ 会考虑不同的边类型 $\phi(s)$ ，以获取同一类型节点对之间的不同关系的语义信息
- 先验张量 $\mu$ 作为注意力向量的自适应缩放，表示元关系三元组（meta relation triplet）$\langle\tau(s),\phi(s),\tau(t)\rangle$ 的权重，描述了不同节点类型和边类型组合的重要程度；$d$ 表示嵌入表示的维度
- $\textbf{Attention}_{HGT}$ 将 $h$ 个注意力头的输出进行拼接，得到每个节点对的注意力向量；最后借助 softmax 函数进行标准化处理，得到每个节点对的最终注意力权重
$\mathrm{K{-}Linear}$ 和 $\mathrm{Q{-}Linear}$ 使得异构相互注意力考虑到了节点类型信息
$W_{\phi(s)}^{ATT}$ 使得异构相互注意力考虑到了边类型信息
这两点是异构相互注意力与普通注意力机制最大的不同
2.1.2 异构消息的传递
Heterogeneous message passing 模型将元关系信息纳入消息的传递过程中 $$ \textbf{Message}_{_{HGT}}(s,e,t) =\underset{i\in[1, h]}{\operatorname*{|}}MSG{-}head^{i}(s, e, t)
$$ $$ MSG{-}head^i(s,e,t)=\text{M{-}Linear}_{\tau(s)}^i\Big(H^{(l-1)}[s]\Big) W_{\phi(s)}^{MSG} $$
- 输入将源节点 $s$ 在第 $l-1$ 层的嵌入表示，然后根据特定的节点类型 $\tau(s)$ 进行 $\text{M{-}Linear}$ 线性映射；矩阵 $W_{\phi(s)}^{MSG}$ 则会考虑到了边类型信息 $\phi(s)$；最后拼接来自不同注意力头的信息
思路和上一小节的 Heterogeneous mutual attention 模块很相似，因此此处不再赘述
2.1.3 基于目标聚合信息
根据每个节点对的注意力得分，聚合邻域内源节点的信息并传递给目标节点： $$ \widetilde{H}^{(l)}[t] = \bigoplus\limits_{\forall s \in N(t)}\Big(\textbf{Attention}_{HGT}(s,e,t)\cdot\textbf{Message}_{HGT}(s,e,t)\Big). $$ 考虑使用注意力得分作为权重，对来自源节点 $s$ 的信息进行加权平均，然后将聚合信息 $\widetilde{H}^{(l)}[t]$ 传递给目标节点 $t$，并得到更新后的嵌入表示 $H^{(l)}[t]$： $$ H^{(l)}[t]=\text{A-Linear}_{\tau(t)}\Big(\sigma\Big(\widetilde{H}^{(l)}[t]\Big)\Big)+H^{(l-1)}[t] $$
- 线性投影函数 $\text{A-Linear}$ 依然是特定于节点类型 $\tau(t)$ 的
- $H^{(l)}[t]$ 表示目标节点 $t$ 在第 $l$ 层的嵌入表示，可直接用于后续的预测任务
2.1.4 相对时间编码
参考了 Transformer 中的相对位置编码，用于适用图动态变化的场景
给定目标节点 $t$ 和源节点 $s$，以及它们对应的时间点 $T(s)$ 和 $T(t)$。则两个节点间的相对位置编码如下： $$ \begin{aligned} \mathrm{Base}(\Delta\mathrm{T} (\mathrm{t},\mathrm{s}),2\mathrm{i})& =\sin\left(\Delta\mathrm{T_{t,s}}/10000^{\frac{2\mathrm{i}}{\mathrm{d}}}\right) \\ \mathrm{Base}(\Delta\mathrm{T} (\mathrm{t},\mathrm{s}),2\mathrm{i}+1)& =\cos\left(\Delta\mathrm{T}_{\mathrm{t,s}}/10000^{\frac{2\mathrm{i}+1}{\mathrm{d}}}\right) \\ \mathrm{RTE}(\Delta\mathrm{T}\left(\mathrm{t},\mathrm{s}\right))& =\text{ T-Linear ( Base (}\Delta\mathrm{T_{t,s}})) \end{aligned} $$
- 上式使用了一组固定的正弦函数作为基，对时间信息进行初步编码
- 然后用 T-Linear 作为线性投影矩阵，对基进行变换，最终得到时间编码
实际使用时，会将时间编码直接添加到源节点 $s$ 的嵌入表示中： $$ \hat{H}^{(l)}[t]=H^{(l)}[t]+\mathrm{RTE}(\Delta\mathrm{T}\left(\mathrm{t},\mathrm{s}\right)) $$
2.1.5 HGSampling 异构子图采样
核心思想：为每个节点类型 $\tau$ 保留单独的节点预算 $B[\tau]$ ，并使用重要性采样策略对每种类型的相同数量的节点进行采样以减少方差。从而在最大化减少信息损失的同时为每种类型保留相似数量的节点和边
HGSampling 异构子图采样的算法图示：
(0) 初始化图：随机选择 $P1$ 作为初始节点，初始化每个节点类型的 budgets 集合
(1) 将 $P1$ 节点的邻节点按照节点类型的不同纳入对应的 budgets 集合
(2) 对每个 budgets 集合进行采样，其中节点类型 $\tau$ 的每个源节点 $s$ 的采样概率为 $\frac{B[\tau][s]^2}{||B[\tau]||^2_2}$（比如 P2 节点的采样概率为 $0.25^2/\sqrt{(0.25^2+0.25^2)}=0.5$）；被采样后的节点从对应 budgets 集合中移除
(3) 将被采样节点的邻节点按照节点类型的不同纳入对应的 budgets 集合，注意此时不再考虑之前已经纳入过 budgets 集合的节点
(4) 按照步骤 (2) 的方式进行采样，被采样后的节点从对应 budgets 集合中移除
(5) 重复以上过程 L 次，所有被采样过的节点构成最大深度为 L 的异构子图
对于部分节点（比如特定年份发表的论文），HGSampling 可以保留时间戳 $T$ 以捕获时间依赖性
此处仅针对 HGSampling 异构子图采样进行粗略描述，更多细节请参阅原文
2.2 实验分析
简单总结如下：
- 本文提出的 HGT 在不同异构图任务中均表现优异（超过其他基线）
- HGT 在 CS、Med 和 OAG 数据集上相对 NDCG 平均提高了11%，10% 和 8%
- 在四项任务中，HGT 平均优于 GCN、GAT、RGCN、HetGNN 和 HAN 20%
- 消融实验显示，HGT 的核心组件是异构注意力机制（-4%）和相对时间编码（-2%）
元关系注意力的可视化：
HGT 能够隐式学习为特定下游任务构建重要的元路径