个人笔记

1 基本信息

1.1 课程标题：《MIT18.02多变量微积分》

1.2 授课讲师：Denis Auroux 教授

1.3 授课日期：2007 FALL

1.4 品读时间：初稿成于2014，电子稿成于2022

1.5 整体耗时：约70h

1.6 摘要

第一单元：向量和矩阵（Unit

Read more

1 旋度与力场

关于旋度的前置知识可参考之前的21课时中对于旋度的理解

速度场的旋度描述的是速度中的旋转运动分量，也就是角速度

加速度场的旋度描述的是加速度中的旋转运动分量，也就是角加速度

力场的旋度描述的是力的旋转分量，是扭矩力矩与转动惯性的比例，即单位质量的扭转力矩，更具体的来说： $$curl(\frac{\mathrm{力}}{\mathrm{质}\mathrm{量}})=2\frac{\mathrm{扭}\mathrm{矩}\mathrm{力}\mathrm{矩}}{\mathrm{转}\mathrm{动}\mathrm{惯}\mathrm{性}}$$ 对于保守场$\overrightarrow{F}$来说，力来自于势能，而势能会依据能力守恒定律，转化为动能，因此此时的$\overrightarrow{F}$不会产生用于旋转的分量，即$curl(\overrightarrow{F})=0$

Read more

1 单连通区域

定义单连通区域：区域内的任意一个闭合回路，在该区域内都有一个以它为界的曲面

举例理解：

• 三维空间去除一个原点后，此区域为单连通区域
• 三维空间去除$z$轴后，此区域为非连通区域

拓扑学拓展（通过”独立“环路数对曲面进行初步分类）：

• “甜甜圈”形状（doughnut）曲面：横切得到的环路由于内部存在洞所以找不到曲面，竖切得到的环路无法是任何曲面的边界，这两种”独立“环路都不能用于界定曲面边界
• 莫比乌斯环和克莱因瓶：属于不可定向（no-orientable）曲面，比如莫比乌斯环是单侧曲面，所以无法

Read more

1 斯托克斯定理

关于格林公式的前置知识可参考之前的第22课时内容和第23课时内容

格林公式可以看作斯托克斯（Stokes）定理在$xy$平面下的特例

当$C$为闭合曲线，包围着曲面$S$，则斯托克斯（Stokes）定理可表示如下： $${\oint }_C\overrightarrow{F}\cdot d\overrightarrow{r}=\int {\int }_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{S}=\int {\int }_S(\mathrm{\nabla }\times \overrightarrow{F})\cdot \hat{n}dS$$ 其中向量$\hat{n}$表示曲面

Read more

1 课程回顾

上一节讲解的扩散方程主要由以下两部分组成：

• 物理上，浓度$u$的流动是由高到低的，用$\overrightarrow{F}$描述这种流动（flow）：$\overrightarrow{F}=-k\mathrm{\nabla }u$
• $\overrightarrow{F}$的散度可以描述浓度变化速度。$div\overrightarrow{F}=-\frac{\partial u}{\partial t}$

2 空间线积分

关于平面线积分的前置知识可参考之前的第19课时的内容

假设在空间向量场$\overrightarrow{F}=P\hat{i}+Q\hat{j}+R\hat{k}$的作用下，物体运动轨迹为$c$，则物体的

Read more

1 散度定理的理解

在上一课时中，对于$\overrightarrow{F}=<P,Q,R>$的三维向量场，提出了散度定理： $${∯}_S<P,Q,R>\cdot \hat{n}dS=\int \int {\int }_D(P_x+Q_y+R_z)dV$$

定义三维空间下的$Del$算子：$\mathrm{\nabla }=<\partial /\partial x,\partial /\partial y,\partial /\partial z>$

对于普通三元函数$f$，$\n

Read more

1 通量的计算公式及证明

前情回顾：

• 上一节提出了通量的计算（面积分）：$Flux=\int !!!{\int }_S\overrightarrow{F}\hat{n}dS$
• 示例1针对曲面法向量与向量场平行的特殊情况进行了计算过程展示
• 示例2通过球坐标化的方法，先进行参数的变换，再进行后续的计算

以上的两种示例都属于现实中的特殊情况，本节课程则提出了更为通用的计算方法： $$Flux=\int \! \! \! \int _S\vec{F}\hat{n}dS=\pm \int \! \! \! \int _S\vec{F}\

Read more

1 三维向量场

与平面向量场类似，只不过维度为三： $$\overrightarrow{F}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}=<x,y,z>$$

2 通量与面积分

三维向量场下的通量 - 描述单位时间内流体场$\overrightarrow{F}$通过表面$S$的流量： $$Flux=\int {\int }_S\overrightarrow{F}d\overrightarrow{S}=\int {\int }_S\overrightarrow{F}\hat{n}dS$$

• 其中$\hat{n}$为面$S$的法向量
• $dS$表示面积积元，和实际的切分方式有关
• 常通过

Read more

1 球坐标系下的三重积分

球坐标系是三维坐标系的一种，以坐标原点为参考点，点$P$的坐标由方位角$\theta$（线$OP$投影到$xy$平面后与$x$轴的夹角）、仰角$\varphi$（线$OP$与$z$轴的夹角）和距离$\rho$（点到原点的距离）构成。经纬度就是球坐标系的一种常见形式，其中$\theta$与经度相似，$\varphi$与维度相似。

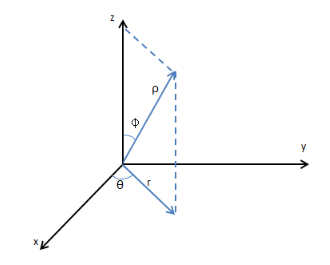
球坐标化通过以下公式实现从$(x,y,z)$到$(\rho ,\varphi ,\theta )$的转化： $$\begin{equation} \left

Read more

1 直角坐标系下的三重积分

二重积分的几何意义是面积，三重积分的几何意义是体积，二者的计算也是可以类推的

举例：计算两个曲面$z=x^2+y^2$和$z=4–x^2–y^2$围成的图形的体积

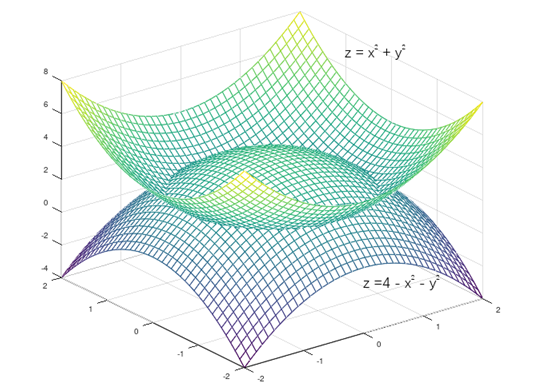
根据$x^2+y^2\le 4–x^2–y^2$推得$x,y$的限制条件：$x^2+y^2\le 2$

将限制条件转化为积分上下限，可得以下计算公式： $$\int \! \! \! \int \! \! \! \int_R fdV=\int_{-\sqrt{2}}^{\sqrt{

Read more