中文标题:使用 AlphaFold 进行高精度蛋白质结构预测
英文标题:Highly accurate protein structure prediction with AlphaFold
发布平台:Nature
发布日期:2021-08-26
引用量(非实时):15560
DOI:10.1038/s41586-021-03819-2
作者:John Jumper, Richard Evans, Alexander Pritzel, Tim Green, Michael Figurnov, Olaf Ronneberger, Kathryn Tunyasuvunakool, Russ Bates, Augustin Žídek, Anna Potapenko, Alex Bridgland, Clemens Meyer, Simon A. A. Kohl, Andrew J. Ballard, Andrew Cowie, Bernardino Romera-Paredes, Stanislav Nikolov, Rishub Jain, Jonas Adler, Trevor Back, Stig Petersen, David Reiman, Ellen Clancy, Michal Zielinski, Martin Steinegger, Michalina Pacholska, Tamas Berghammer, Sebastian Bodenstein, David Silver, Oriol Vinyals, Andrew W. Senior, Koray Kavukcuoglu, Pushmeet Kohli, Demis Hassabis
关键字: #蛋白质预测 #AlphaFold #DeepMind
文章类型:journalArticle
品读时间:2023-10-25 16:45
1 文章萃取
1.1 核心观点
AlphaFold 通过结合新颖的Transformer 神经网络架构和基于蛋白质结构的进化、物理和几何约束的训练程序,极大地提高了结构预测的准确性。
Evoformer 模块通过注意力机制和三角更新机制,完成序列比对(MSA)和结构模板中的信息的交换使得最终的序列抽象表示从而能够直接推理空间和进化关系
结构模块则在蛋白质主链的基础上构建骨干框架,之后通过不变点注意力(IPA)整合所有信息,直接实现原子的3D坐标预测输出,并添加了很多辅助预测头实现更丰富的输出
最后AlphaFold 通过自蒸馏技术进行数据增强,使用回收迭代机制实现自我强化;AlphaFold的预测结果经过严格的实验分析,在保持优越的预测性能的同时模型的稳健性也令人信服
1.2 综合评价
- AI与生物化学领域的交融和突破,里程碑事件
- 技术说明非常细致和全面,诸多细节信息量爆炸
- 多信息融合和物理规则约束等方面的处理也很启发
- 论文细节也展现出了背后团队很强的实验设计和规划能力
- 可能存在过度工程化(部分技巧的作用存疑);部分超参没有充分测试
1.3 主观评分:⭐⭐⭐⭐⭐
2 精读笔记
2.1 背景知识
维基百科 - 氨基酸是构成蛋白质的基本单位
- 氨基酸指一类含有氨基(-NH2)和羧基(-COOH)的有机化合物的统称
- α氨基酸的氨基和羧基连在同一个碳原子上,β氨基酸的氨基和羧基连在相邻的碳原子上
- 在生物学中,氨基酸通常特指α氨基酸;天然蛋白质水解所得的氨基酸大多为α氨基酸
- 在生物化学上,以甘油醛为基准依分子的绝对构型又分:D型和L型(手性,chirality)
维基百科 - 蛋白质结构是指蛋白质分子的空间结构:
- 作为一类重要的生物大分子,蛋白质主要由碳、氢、氧、氮、硫等化学元素组成
- 所有蛋白质都是由20种不同的L型α氨基酸连接形成的多聚体(聚合物,由许多以共价键相连且重复的单体或结构单元组成分子量很大的化合物),在形成蛋白质后,这些氨基酸又被称为残基
- 蛋白质的结构决定了其功能、与其他分子的相互作用、调节、稳定性和所有其他相关特性
- 了解蛋白质的结构与医疗和生物有紧密关系(比如药物阻断或激活、生物功能调节与稳定)
扩展阅读:
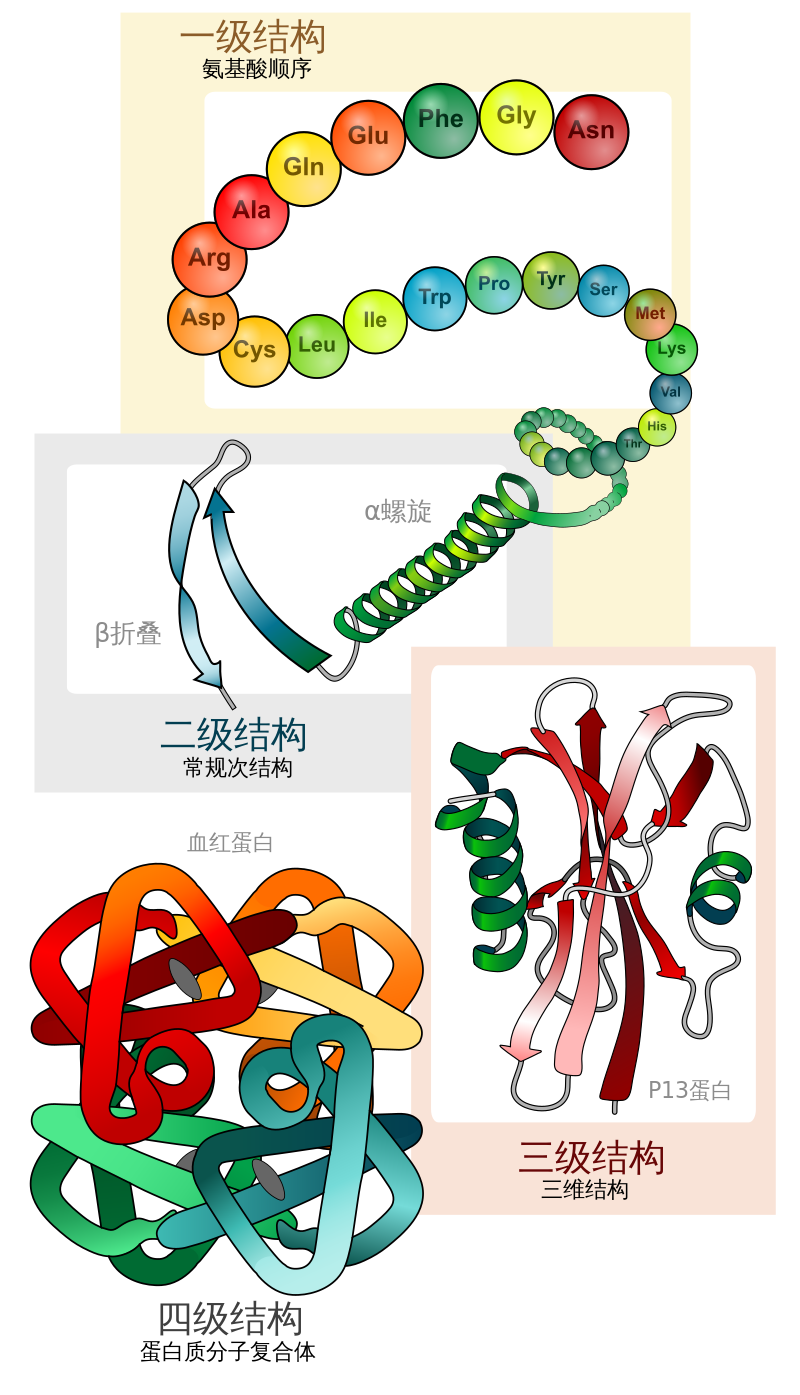
- 蛋白质一级结构:组成蛋白质多肽链(包含多个肽键 -CO-NH-)的线性氨基酸序列
- 蛋白质二级结构:依靠不同氨基酸之间的C=O和N-H基团间的氢键形成的稳定结构,主要为α螺旋和β折叠
- 蛋白质三级结构:通过多个二级结构元素在三维空间的排列所形成的一个蛋白质分子的三维结构
- 蛋白质四级结构:用于描述由不同多肽链(亚基)间相互作用形成具有功能的蛋白质复合物分子
已知蛋白质序列有数十亿,其中只有大约100,000种独特蛋白质的结构被确定
CASP(全球蛋白质结构预测评估竞赛)评估:
- 每两年使用最近确定的未公开蛋白质结构进行一次评估
- 是对预测方法的盲测,长期以来一直是结构预测准确性评估的金标准
- 在第13届CASP中第一代AlphaFold以58%的准确率遥遥领先第2名(17%)
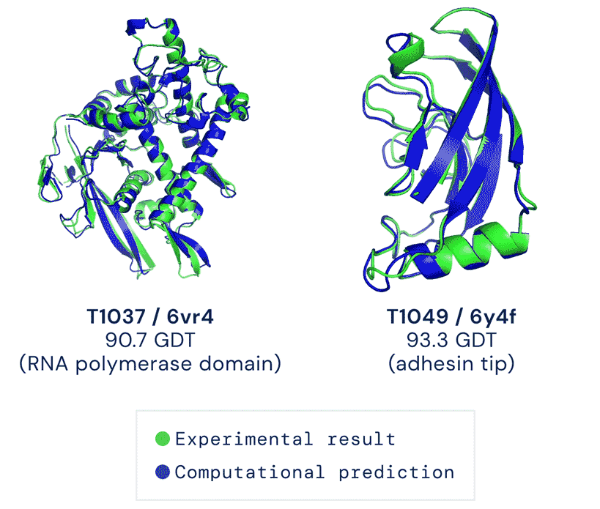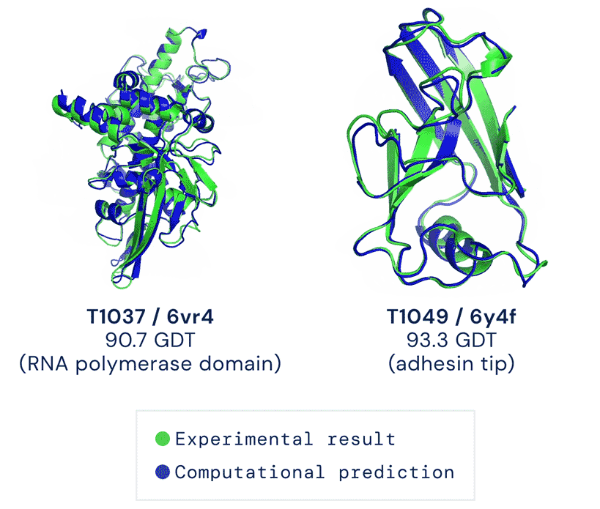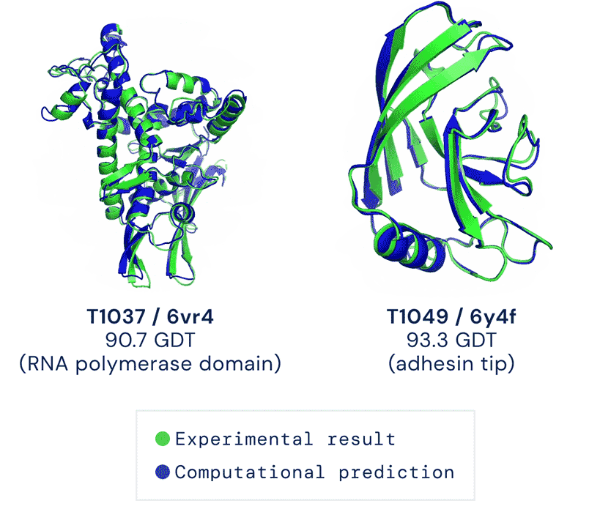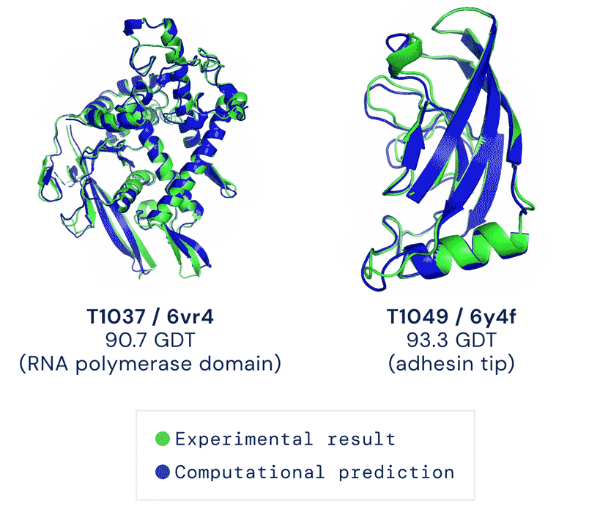
- 在第14届CASP中,本文提出的AlphaFold 2直接将准确性拔高到了92.4%
- 补充:一般认为评分大于90是可接受的,而92.4是 AlphaFold 2的评分中位数
- 序列比对(sequence alignment,SA)是一种排列 DNA、RNA 或蛋白质序列以识别相似区域的方法
- 多重序列比对(MSA)指三个或更多生物序列(蛋白质、DNA或RNA)的序列比对的过程或结果
- 一组哺乳动物的组蛋白(histone,染色质的主要蛋白质组分)序列比对如下所示:

在上图最后一行中,
*表示保守序列(conserved),:表示保守突变(Conservative),.表示半保守突变(Semi-Conservative),表示非保守突变(Non-Conservative)
蛋白质结构的主链和侧链 by GPT4:
- 主链:由连续的氨基酸残基通过肽键形成的线性结构。主链包含每个氨基酸的氨基(NH2)、羧基(COOH)和α-碳原子(与氨基、羧基和侧链相连的碳原子)。主链是构成蛋白质骨架的主要部分,决定了蛋白质的一级结构(氨基酸序列)和二级结构(如α-螺旋和β-折叠)。
- 侧链:侧链或R基团是氨基酸的一部分,与α-碳原子相连,不同的氨基酸有不同的侧链。侧链的化学性质和结构决定了氨基酸的性质,如极性、酸碱性和疏水性等,因此对蛋白质的三维结构和功能有重要影响。侧链可以参与蛋白质的相互作用,如离子键、氢键、范德华力和疏水相互作用等
蛋白质结构的扭转角 by GPT4+wiki:
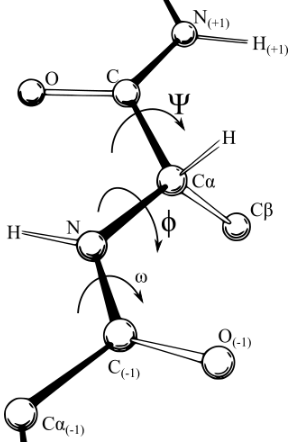
- 二面角(dihedral angle)是指两个相交平面之间的夹角;扭转角(torsion angle)是二面角在化学中的特例,描述了通过化学键连接的分子的两个部分的几何关系
- 在蛋白质的主链中,每个氨基酸残基都有两个扭转角,一个是$\Phi$角,另一个是$\Psi$角。$\Phi$角是指C-N键围绕的扭转角,而$\Psi$角是指N-Cα键围绕的扭转角。
- 在某些文献中,$\Omega$角也会被考虑,它是指Cα-C键围绕的扭转角,但在理想的蛋白质结构中,$\Omega$角通常被认为是固定的(约180度),因此主要考虑$\Phi$和$\Psi$两个角
- 侧链的$\chi$角描述了侧链中的原子之间的相对位置和取向。具体来说,$\chi$角是定义在侧链中四个连续原子之间的扭转角。侧链中的每个$\chi$角都对应一个特定的键的旋转
- 在自然存在的20种氨基酸中,侧链最多只有四个$\chi$角(理论上可能会有更多)
2.2 模型结构
AlphaFold 在神经网络架构的基础上融合了基于蛋白质结构的进化、物理和几何约束:
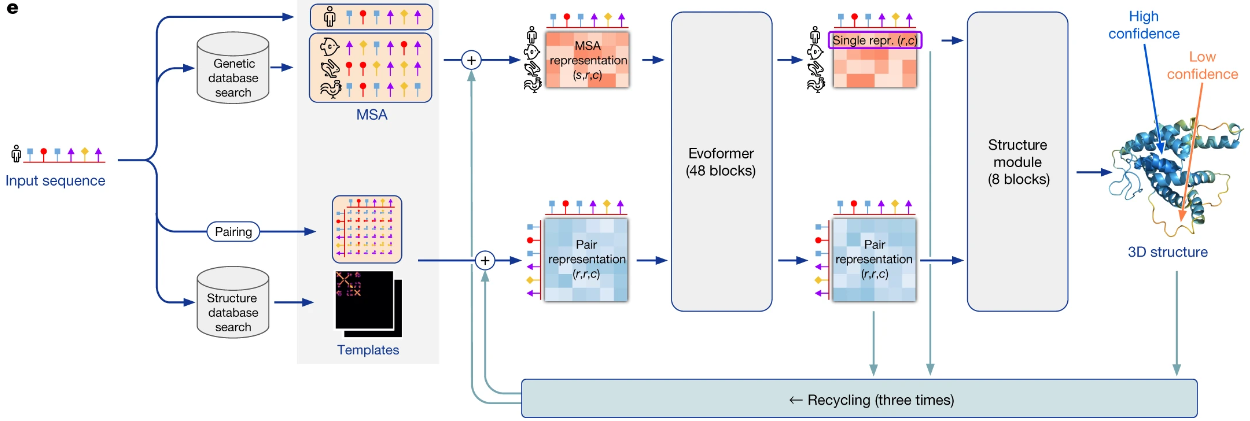
- AlphaFold 使用一级氨基酸序列和同源物比对序列(MSA)作为第一部分输入;而第二部分输入是将已知相似序列的蛋白质三维结构作为模板(Templates),并与结构未知的输入一级序列进行配对(pairing)
- 模型输出为给定蛋白质的所有重原子(除氢以外的任何原子)的 3D 坐标
- 模型先将比对序列(MSA)和配对(pairing)模板分别进行嵌入表示(representation)
- 之后模型通过 Evoformer 神经网络块实现空间和进化关系的推理,然后结构模型(Structure module)将最终表示作为输入,预测所有重原子(除氢以外的任何原子)的 3D 坐标和每个残基的置信度
- 预测结果会作为新的模板回收迭代到整个建模预测过程,重复三次后的结果精度有明显提高
2.2.1 数据预处理
AlphaFold 需要多个遗传(序列)数据库才能运行:
- BFD(Big Fantastic Database,最大的开源蛋白质家族集合之一):用于查找MSA
- MGnify(微生物组序列数据分析资源):用于查找MSA
- PDB70(包含完整蛋白质结构,聚类后序列同一性<70%):用于模板的搜索
- PDB (以mmCIF 格式存储蛋白质结构):用于模板的搜索
- PDB seqres:只用于预测两条以上蛋白质链结构(AlphaFold-Multimer)
- UniRef30 (FKA UniClust30)(聚类后序列同一性水平为30%):用于查找MSA
- UniProt:只用于预测两条以上蛋白质链结构(AlphaFold-Multimer)
- UniRef90(聚类后序列同一性水平为90%):用于查找MSA
完整数据库的总下载大小约为 556 GB,解压后的总大小为 2.62 TB
序列和模板的搜索:
- 输入氨基酸序列需要满足 FASTA 格式(其中的核酸或氨基酸均以单个字母编码呈现)
- AlphaFold 使用开源工具 JackHMMER v3.3) 和 HHBlits v3.0-beta.3 搜索遗传数据库中的序列
- 蛋白质结构模板一般满足 mmCIF 格式(包含序列、原子坐标、发布日期、名称和分辨率)
- AlphaFold 使用开源工具 HHSearch来搜索遗传数据库中的蛋白质结构模板
- 结构模板对应的序列不能是输入序列的子集,也不能太短(残基小于10或输入序列的10%)
- 推理时模板限制为最多4个;训练时可用模板最多保留20个(再随机选择抽选最多4个)
根据简单调研,以上提到的工具似乎都是基于隐马尔可夫模型 (HMM)的序列搜索工具
训练数据的过滤和采样:
- 输入 mmCIF 的分辨率限制为小于 9 Å(排除大约 0.2% 的样本)
- 不考虑与输入一级序列中单一氨基酸占比超过80%的期刊(排除大约 0.8% 的样本)
- 训练样本的采样概率与该链所在簇的大小成反比(增加多样性,减少同质化)
- 训练样本的采样概率与该链的长度成正比(平衡长度分布,重视长链的训练)
百度百科 - 埃米(外文名Ångstrom或ANG或Å)是晶体学、原子物理、超显微结构等常用的长度单位,音译为"埃",符号为Å,1Å等于10-10m,即纳米的十分之一
自蒸馏数据集:
- 训练样例有 25% 来自蛋白质数据库的已知结构,有 75% 来自自蒸馏集
- 首先从Uniclust30数据集中筛选出的MSA(筛选标准:序列长度在200~1024之间,序列数大于200,同一序列在不同的MSA中重复出现时需要删除该序列)
- 然后在 PDB 数据集上单独训练模型,并预测筛选出的MSA中355,993 个序列的蛋白质结构,以此预测结果作为“伪标签”创建一个结构数据集以在训练时使用
- 对于每个预测残基,通过计算与其他残基的距离分布与参考分布之间的 KL 散度来实现置信度度量
- 训练时会屏蔽掉置信度低于0.5 的残基;参考分布则来自序列的随机采样(1000个序列)
参考分布对应的采样距离分布似乎还需要有单独的模型来预测(距离分布)?
MSA 预处理:
- 在MSA 中随机删除连续的序列块,增强数据的多样性和模型的泛化能力
- 对MSA 序列进行聚类(偏向于选择彼此远离的样本),保持多样性的同时减少计算成本
- 聚类过程中,还会对MSA 聚类中心的每个氨基酸(以15%的概率)进行随机掩码
- 未被选为聚类中心的MSA序列,也会随机采样后作为”额外“的MSA 特征输入模型
- 实际训练中,MSA的聚类和掩码过程会重复进行(重采样),以增强模型的泛化能力
残基裁剪:输入序列的残基维度被裁剪到一个连续的区域(最大长度为$r$)
2.2.2 输入嵌入层
最终的模型主要输入(更多细节可参阅原始论文的拓展资料中Table1):
- target_feat:维度为$[r, 21]$,表示裁剪后的输入一维序列
- residue_index:维度为$[r]$,表示裁剪前的原始序列索引(位置编码)
- msa_feat:维度为$[s_c, r, f_c=49]$,表示聚类(簇数为$s_c$)后的已经过随机掩码的MSA序列及其衍生特征(MSA块的删除情况、簇中每个残基的氨基酸类型分布等)
- extra_msa_feat:维度为$[s_c, r, f_e=25]$,表示未被选为聚类中心的MSA序列的额外采样特征(MSA块的删除情况、经过随机掩码的每个残基的氨基酸类型)
- template_pair_feat:维度为$[s_t, r, r, f_p = 88]$,表示$s_t$个结构模板对应的成对(pair)序列信息(随机掩码后)、残基之间对应的距离位置关系(离散化距离,位移单位向量)
- template_angle_feat:维度为$[s_t, r, f_a=51]$,表示$s_t$个结构模板对应每个残基的扭转角(3 个主链扭转角和最多 4 个侧链扭转角)、替代扭转角和相关掩码信息
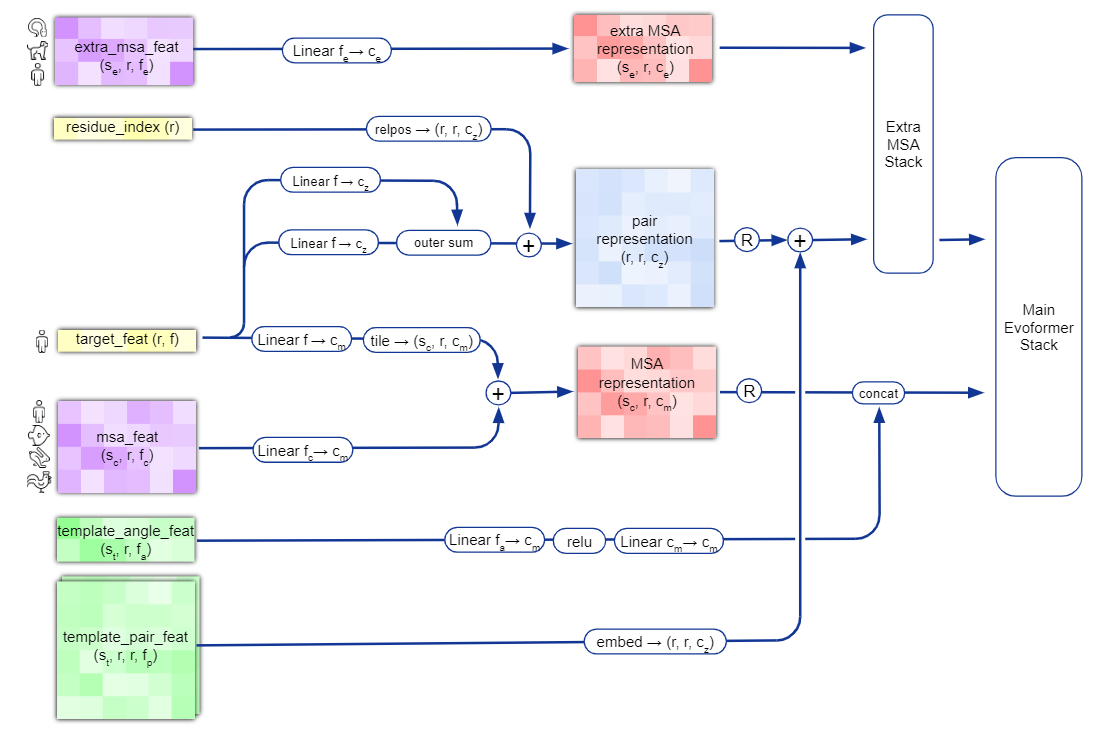
- 其中
Linear表示普通线性层;relpos表示相对位置编码 outer sum表示矩阵加法,tile表示数组复制(增加维度)relu和R均表示Relu激活函数;concat表示矩阵拼接- 上图中的通道数$c_m$、$c_z$和$c_e$分别为256、128和64
- 结构模板信息
template_pair_feat的嵌入表示会在2.2.4.1单独说明 - 额外MSA特征
Extra MSA Stack的处理会在2.2.4.2单独说明
2.2.3 Evoformer块
网络的主干由 Nblock = 48 个 Evoformer 块组成
- 每个块都有一个 MSA 表示 $m_{si}$ 和一个配对表示 $z_{ij}$ 作为其输入
- 每个层的输出都通过一个残差连接添加到当前的表示中;部分层输出包含Dropout
- 最后的 Evoformer 块提供了一个高度处理的 MSA 表示 $m_{si}$ 和一个配对表示 $z_{ij}$
Evoformer块核心流程:
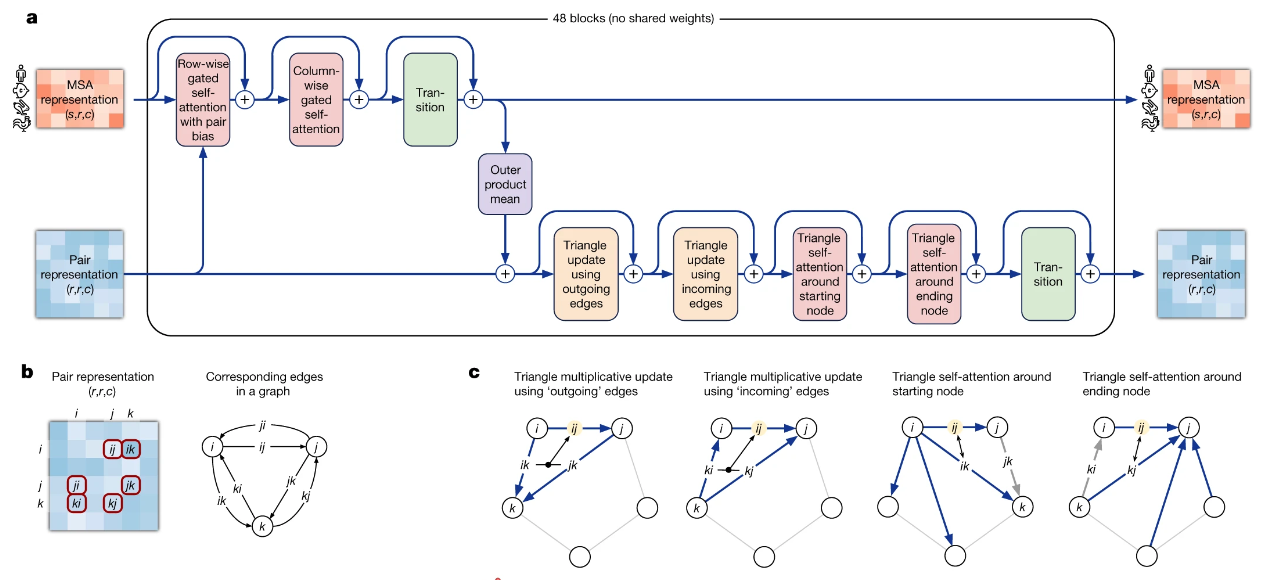
Row-wise gated self-attention with pair bias:在逐行自注意力块的基础上,将来自配对表示的信息作为附加偏差项整合到注意力权重中(鼓励通信,增强一致性);同时对输出信息使用门控机制调控Column-wise gated self-attention:和上一个很像的逐列自注意力块,只是缺少配对表示的信息整合Transition:一个 2 层 MLP 作为过渡层,通道数扩展为原来的4倍(左3)或2倍(右1)Outer product mean:使用 MSA 表示来更新配对表示(两个独立的线性变换+投影后取均值)Triangular multiplicative update using outgoing edges:将配对表示矩阵转化为图结构,用三角形两边的信息来更新第三条边(实际上是对配对表示的局部更新)Triangular multiplicative update using incoming edges:同上,只是将”出边“改为”入边“Triangular gated self-attention around starting node:在自注意力块的基础上,将起始节点$i$为query,周围的边信息作为key、value和注意力权重的偏差项;同时对输出信息使用门控机制调控Triangular gated self-attention around starting node:同上,只是将起始节点$i$改为结束节点$j$
蛋白质的3D结构需要满足很多约束,比如距离上的三角不等式;三角更新方法的诞生也是基于这种直觉
三角乘法更新最初是作为三角自注意力的平替而开发的,二者均可以产生高精度的结构;在Evoformer块的实际执行过程中,将两种更新方法进行了结合(效果更好)
为了兼容三角形缺失边的情况,在注意力计算中还会添加额外的布尔型偏置项(标识是否缺失)
2.2.3.1 细节1:门控自注意力
以Row-wise gated self-attention with pair bias为例
流程图:
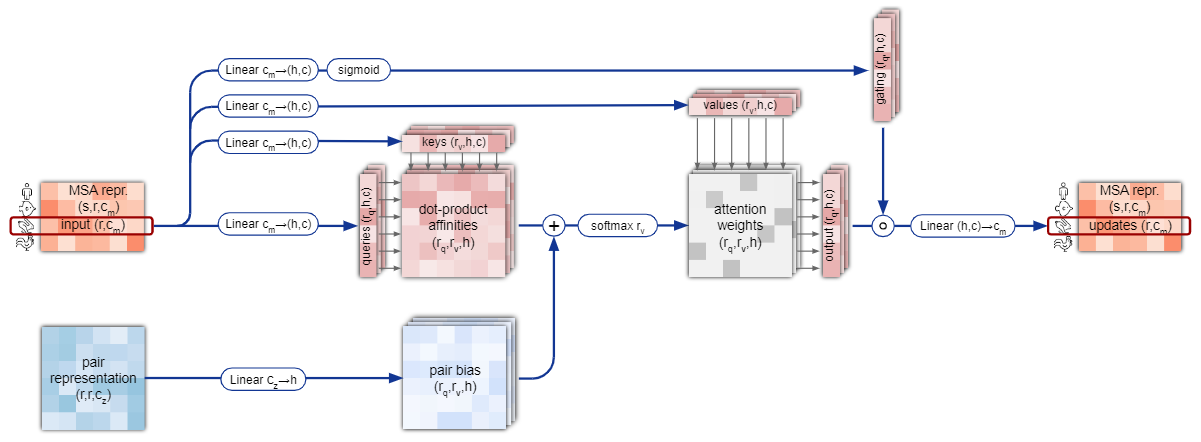
伪代码:

2.2.3.2 细节2:外积均值
Outer product mean
伪代码:

2.2.3.3 细节3:三角乘法更新
以Triangular multiplicative update using outgoing edges为例
流程图:
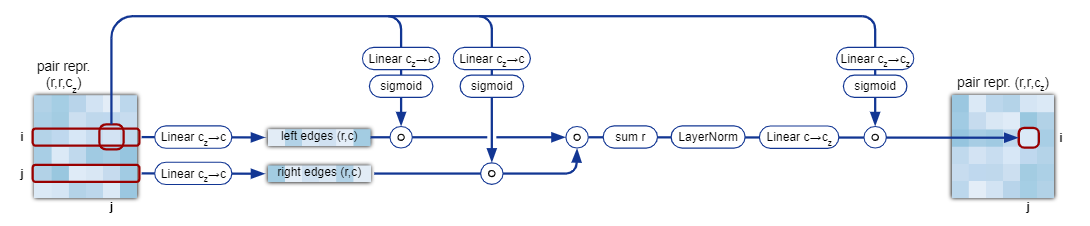
- 左边集合(left edges)定义为$\Sigma_k{ik}$;右边集合(right edges)定义为$\Sigma_k{jk}$
伪代码:

注:伪代码对边信息进行了简化,源代码有明确区分 left edges 和 right edges
2.2.3.4 细节4:三角自注意力
以Triangular gated self-attention around starting node为例
流程图:
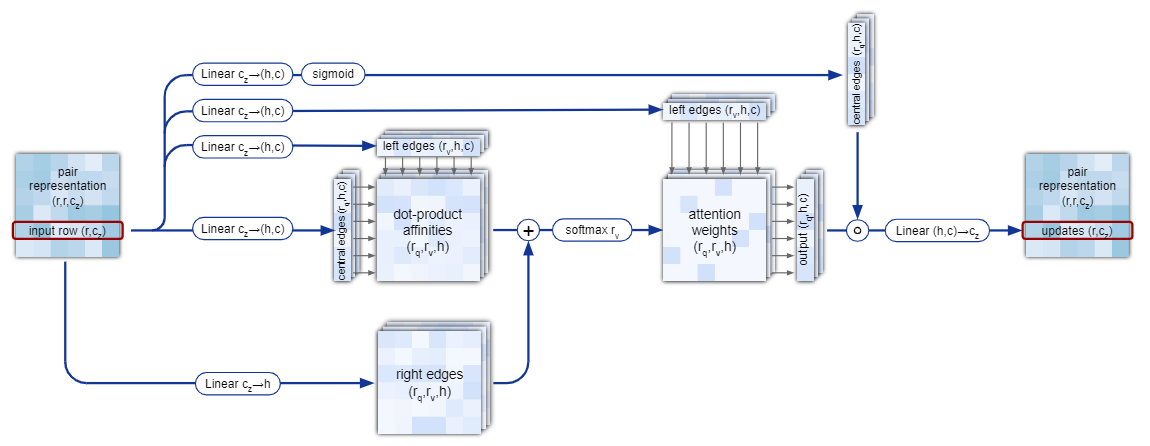
伪代码:

注:伪代码对边信息进行了简化,但源代码也没有明确区分 left edges 和 right edges?
2.2.4 其他附加模型块
额外的模型块包括结构模板的嵌入表示和非聚类 MSA 序列的处理
2.2.4.1 结构模板特征处理
结构模板特征处理主要包含两部分:
- 针对初始的配对模板表示$t_{s_t,i,j}$进行初步处理(Dropout和三角更新)

- 三角更新包括三角自注意力和三角乘法更新,不同模板之间参数共享
Transition是一个 2 层 MLP 的过渡层,通道数扩展为原来的2倍
- 以逐点自注意力的形式将配对模板信息$t_{s_t,i,j}$融入到配对信息$z_{ij}$

query为初始的$z_{ij}$,目前主要包含输入一维序列和位置信息key和value为已经过处理的配对模板表示$t_{s_t,i,j}$- 更新后的$z_{ij}$将包含配对信息,并作为主Evoformer块的输入
2.2.4.2 非聚类 MSA 处理
模块Extra MSA包含了非聚类 MSA 的处理过程
模块Extra MSA和主Evoformer块很相似,差异点如下:
- 输入的MSA表示改为非聚类MSA表示
- 主Evoformer块有48块,而
Extra MSA块是4 - 逐行的门控自注意力输出的通道数从32改为8
- 逐列的门控自注意力中的
query从改为全局均值
Extra MSA Stack模块的计算复杂度更低,也更重视对全局信息的提取
2.2.5 结构模块
上一节中,Evoformer块输出的是蛋白质结构的抽象表示
而结构模块(Structure module)将其映射到具体的3D原子坐标
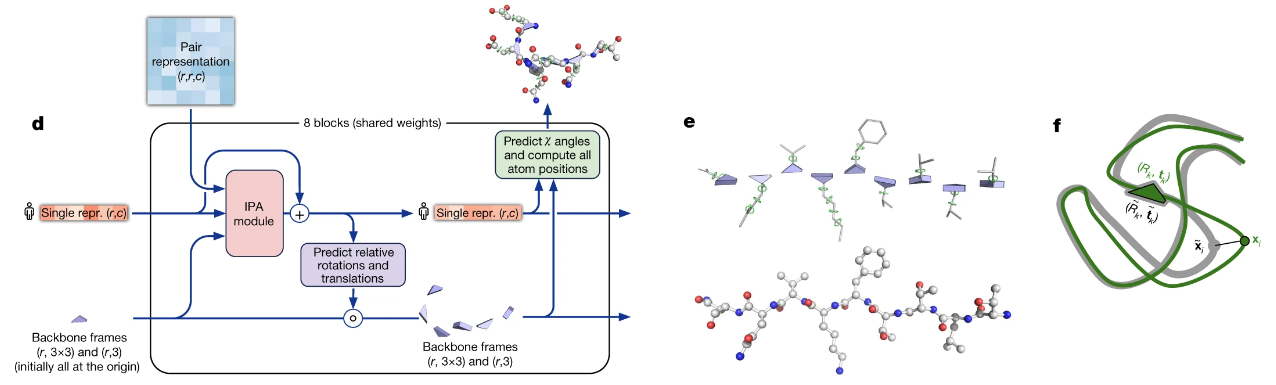
- 图(d)展示了结构模块的核心流程,其包含8个参数共享的网络块
- 图(e)展示了蛋白质主链(residue gas),上部分为一个自由浮动的主链刚体(蓝色三角形)和侧链的 χ 角(绿色圆圈);下部分为该序列对应的原子结构(红:低能,白:中能,蓝:高能——网络资料)
- 图(f)最终的预测结构(绿色)和真实结构(灰色)的对比;$(R_k,t_k)$表示框架(backbone frames);其中的每个预测点$x$的帧对齐点误差(FAPE)构成了最终的预测损失
结构模块的核心流程说明:
- 初始化:对主链进行黑洞初始化(black hole initialization),将所有残基都置于同一个点(原点)并保持相同的方向;对于最终的原子坐标,扭转角是唯一的自由度,而所有键角和键长都是完全刚性的
- 更新序列的抽象表示:通过不变点注意力(Invariant Point Attention,IPA)模块和过渡层来实现更新,IPA块输入包括配对表示、序列表示和从局部骨干框架抽取的位置信息;IPA块能确保最终输出对于全局的旋转和平移是不变的(即,全局的旋转和平移操作不影响输出值)
- 更新骨干框架:基于更新后的单一序列表示通过预测给出骨干的具体更新帧(一系列的旋转矩阵和平移向量),然后实现对骨干框架(第n个骨干坐标由前n-1个更新帧累积而成)的调整
- 坐标计算:基于结构模块预测给出的骨干框架和扭转角,然后模型通过将扭转角应用于具有理想化键角和键长的相应氨基酸结构来构建原子坐标(期间刚性基团约束也会附加到局部框架中)
结构模块这一部分的关键创新包括打破链结构以允许同时对结构的所有部分进行局部细化、一种新颖的等变变压器以允许网络隐式推理未表示的侧链原子以及一个损失项,该损失项将大量的残基方向正确性的权重。在结构模块内和整个网络中,我们通过重复将最终损失应用于输出,然后将输出递归地输入到相同的模块中,来强化迭代细化的概念。使用整个网络的迭代细化(“回收”)显着地提高了准确性,并且只需要少量的额外训练时间
2.2.5.1 细节1:刚性基团与骨干框架
刚性基团意味着,这些原子群的扭转角在某种程度上是固定的,不容易发生改变
“刚性”是相对的,并不意味着扭转角完全不能改变(只是一般不改变,或者改变较小)
20种氨基酸对应的所有对扭转角存在依赖性的原子(刚性基团):
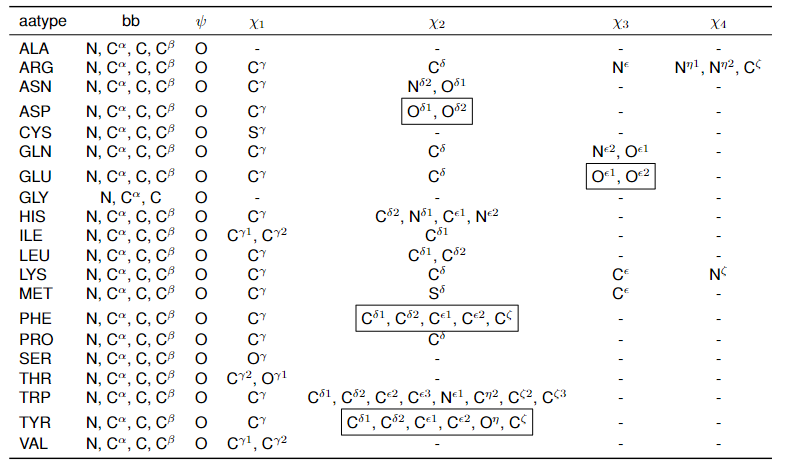
bb表示仅依赖于骨干框架的原子(“骨架刚性群”);黑框中的组具备180°旋转下的对称性- 需要注意的是:没有重原子的位置取决于扭转角$\Omega$或$\Phi$(所以上图没有这两列)
骨干框架,即主链框架(由连续的氨基酸残基通过肽键形成的线性结构)的抽象表示
骨干框架由一系列的更新帧组成: $$T_i=(R_i,\vec{t}_i)=T_{i-1} \ \text{o} \ (R_{i-1},\vec{t}_{i-1})$$
- 其中$R$表示旋转矩阵,$\vec{t}$表示位移向量
- 原始向量$\vec{x}_0$的旋转和位移可表示为:$\vec{x}_1=R\vec{x}_0+\vec{t}$
- 连续两个更新帧的组合可表示为:$(R_1,\vec{t}_1) \ \text{o} \ (R_2,\vec{t}_2)=(R_1R_2,R_1\vec{t}_2+t_1)$
在本文中,骨干框架的预先设定还能为侧链位置提供高度约束
最后,论文还定义了函数用于实现3D坐标到更新帧的转换:

- 该函数借助Gram-Schmidt正交化,能从子空间快速获得对应的标准正交基
- 对于主干框架,论文使用 N 作为$\vec{x}_1$,Cα为$\vec{x}_2$,C为$\vec{x}_3$,所以框架中心为Cα
- 对于侧链框架,按照原子距离主链的远近分别定义为$\vec{x}_1$,$\vec{x}_2$,$\vec{x}_3$
脑洞:魔尺(Rubik's Snake)的运动≈只考虑了旋转的简化版骨干框架
2.2.5.2 细节2:不变点注意力(IPA)
Invariant Point Attention(IPA)模块的流程图:
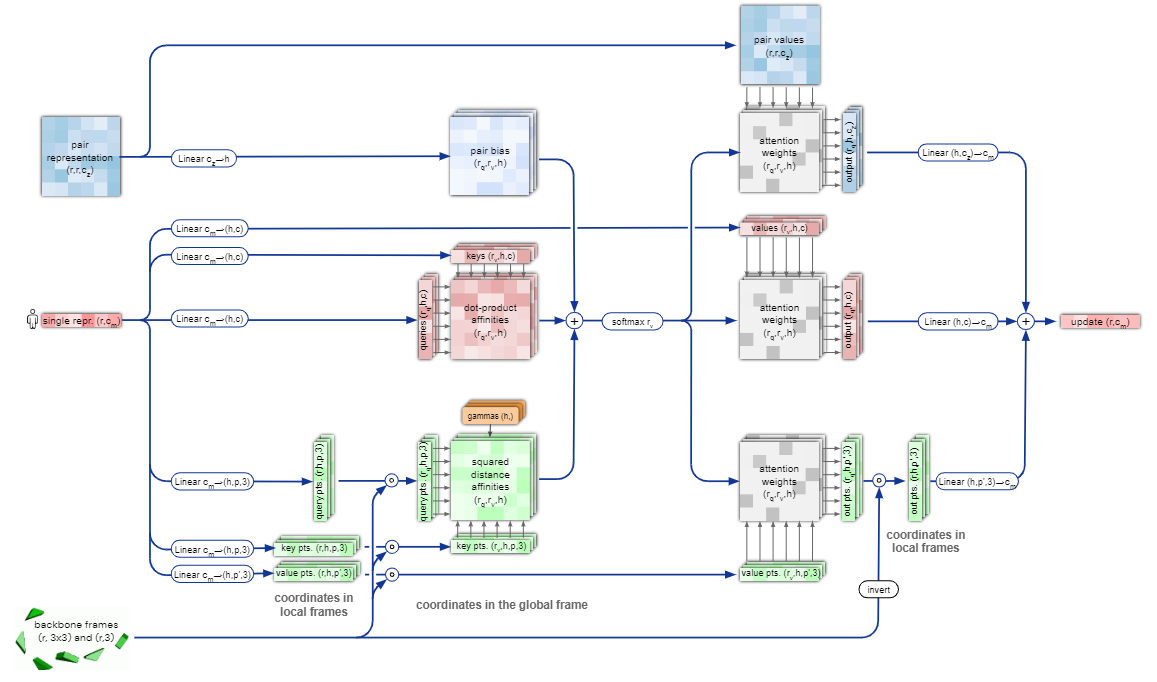
- 从上至下,蓝色部分为配对表示(包含相关序列及其蛋白质结构信息),红色部分为序列表示(包含输入序列的深度抽象信息),绿色部分为不变点注意力(包含框架信息)
- 总的来说,三个表示会先分别调整,然后将注意力加权汇总后,得到
attention weights(灰色部分);该注意力会分别指导更新三个输入表示,最终汇总输出完成序列表示的更新
Invariant Point Attention(IPA)模块的伪代码:

- $W_C$和$W_L$作为权重,平衡不同注意力项的权重(确保不同项的贡献一致)
- 向量的L2范数是确保IPA在全局刚性变换(旋转或平移)下是不变的
此处权重值的确定,尚未仔细研究;根据原文来看,是假设
query和key都服从标准正态分布后,得到的注意力值的方差$Var[0.5\times ||q||^2-q^Tk]$;然后令方差=1来确定权重值
2.2.5.3 细节3:骨干框架的更新与其他
经过了Evoformer块和IPA块处理后的序列表示$s_i$已经包含了足够的信息
因此序列表示$s_i$可作为输入直接给出预测旋转的四元数和位移向量
骨干框架更新的伪代码:

三维空间中,一个旋转可以由一个轴$v=[x,y,z]$和一个关于该轴的旋转角度$\theta$来定义,也就是四元数;四元数以更紧凑的方式表示三维空间中的旋转
本文中,默认四元数的第一项为1;(原因还没琢磨清楚,但原文描述该方式保证了一个有效的归一化四元数,并且使得旋转角度更倾向于小旋转而不是大旋转?)
其他优化1:重命名对称真实原子(忽略部分细节)
- 部分刚性集团存在180°旋转的对称性而导致的原子名称不明确
- 此时需要根据最终的预测误差,以全局一致的方式解决命名歧义
其他优化2:Amber relaxation(细节尚未理解)
- Amber relaxation主要用于解决剩余结构中可能存在的违规和冲突
- 具体过程:使用OpenMM 模拟包执行完全能量最小化来放松模型的预测,之后根据最小化器的收敛表现判断哪些残基存在违规;之后去除相关残基中的原子约束,再次执行最小化过程
- 重复以上过程,直到解决所有的违规问题
GPT4:能量最小化(或能量弛豫)就是通过改变系统中的原子位置,寻找一种结构配置,使得系统的总能量达到最小;系统的能量是由一系列相互作用项的总和来计算的,包括键长、键角、扭转角、范德华力和静电相互作用等
在蛋白质结构预测和优化中,能量最小化常常被用来纠正违规的结构。由于每种蛋白质的稳定结构对应的能量通常较低,如果一个结构中存在违规(例如键长或键角与理论值相差太大),那么这个结构的能量通常会较高。通过能量最小化,可以找到一种新的结构配置,使得能量降低,从而纠正这些违规的地方。
需要注意的是,能量最小化并不能保证找到全局最小能量的结构,因为这是一个典型的NP-hard问题。在实际应用中,通常使用一些启发式的优化算法(例如模拟退火)来寻找局部最小值。
2.2.6 损失函数和辅助损失
AlphaFold网络的训练是端到端的,损失函数如下:
$$\mathcal{L}=\begin{cases}0.5\mathcal{L}_{\mathrm{FAPE}}+0.5\mathcal{L}_{\mathrm{aux}}+0.3\mathcal{L}_{\mathrm{dist}}+2.0\mathcal{L}_{\mathrm{msa}}+0.01\mathcal{L}_{\mathrm{conf}}&\text{training} \\0.5\mathcal{L}_{\mathrm{FAPE}}+0.5\mathcal{L}_{\mathrm{aux}}+0.3\mathcal{L}_{\mathrm{dist}}+2.0\mathcal{L}_{\mathrm{msa}}+0.01\mathcal{L}_{\mathrm{conf}}+0.01\mathcal{L}_{\mathrm{exp~esolved}}+1.0\mathcal{L}_{\mathrm{viol}}&\text{fine-tuning}\end{cases}$$
- 主损失$\mathcal{L}_{\mathrm{FAPE}}$来自帧对齐点误差(FAPE),该误差主要来自逐帧坐标之间的距离误差,FAPE损失是对所有主链和侧链框架中的所有原子的评分(实际计算时会进行截断,误差上限为10Å)
- $\mathcal{L}_{\mathrm{aux}}$是结构模块的辅助损失,包含中间结构的平均FAPE损失和扭转角损失;扭转角损失的计算方式使用角度间差值的L2范数(在数学上等价于角差的余弦)
- $\mathcal{L}_{\mathrm{dist}}$是分布预测的平均交叉熵损失,预测目标是残基距离的分布分箱(直方图)
- $\mathcal{L}_{\mathrm{msa}}$是屏蔽 MSA 预测平均交叉熵损失,主要考虑了23种类型预测,其中包括:20种常见的氨基酸类型、未知类型、缺失标识、掩码标识
- $\mathcal{L}_{\mathrm{conf}}$是模型置信度损失,该损失来自模型的置信度预测(pLDDT);实际计算时,会将预测分数进行离散化并构建交叉熵损失(这样模型会直接输出预测结果的置信度)
- $\mathcal{L}_{\mathrm{exp}}$是“实验解析”损失,模型会预测判断原子是否在高分辨率结构中通过了实验解析;该过程仅发生在微调阶段,使用高分辨率 X 射线晶体和冷冻电镜结构构建标准交叉熵
- $\mathcal{L}_{\mathrm{viol}}$是违规损失,促使模型生成合理的结构而避免故障或违规问题;违规损失主要从“合理键长”、“合理键角”和“避免碰撞”三个角度出发;该过程仅发生在微调阶段,避免过早干预而导致预测精度下降
其他细节补充:
- 扭转角损失中还包含一个小的正则项$\mathcal{L}_{\mathrm{anglenorm}}$,用来约束扭转角的预测值接近单位圆;避免向量太靠近原点,导致数值不稳定的梯度;(经验上)改善向量的范数,优化模型的学习效果
- $\mathcal{L}_{\mathrm{conf}}$损失对应的权重特别小,确保pLDDT预测的同时不影响结构预测本身的准确性
- 以上不同损失项的权重确定为手工设计,并且后期优化较少
2.2.7 回收迭代与其他细节
“回收(recycling)”技术:将先前的输出嵌入作为额外的输入
- 回收允许网络更深入地处理输入特征的多个版本(例如合并 MSA 重采样)
- 在推理时,循环产生一个具有共享权重的循环网络,其中每次迭代时接受输入特征输入和前一次迭代的输出,并产生新的细化输出;而初始迭代时的输入“输出”是0
- 在 AlphaFold 模型的训练/推理中,网络进行了4次回收迭代
在实际训练中,AlphaFold 通过控制是否可以进行反向传播的方式,将回收迭代和训练迭代进行区分;然后收集回收迭代时的“输出”,通过采样来提高训练效率
该方式实现计算和内存的改善(额外训练时间从原本的300%降低至37.5%),也增强了模型自我迭代优化的能力(模型会产生更好的“输出”作为下次迭代时的输入)
2.3 实验分析
2.3.1 训练和推理细节
训练分两个阶段进行
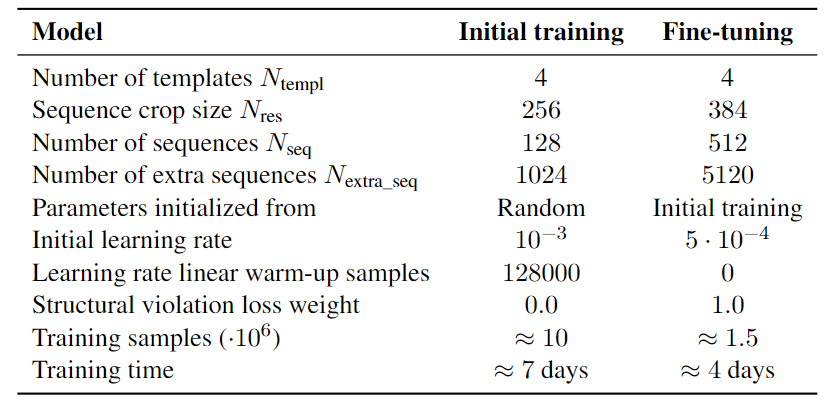
- 第一阶段的序列裁剪后最大长度为256 ,阶段的微调则是 384
- 第一阶段的学习率存在预热;第二阶段的学习率较低并且没有预热
内存占用的优化:
- AlphaFold 模型在训练和推理过程中都具有较高的内存消耗
- 方法1:在前向传递时存储48个 Evoformer 块之间传递的激活;这样在反向传递时,只需重新计算块内的所有激活(将20.25G的内存占用降低到1.7G,但训练时间增加了33%)
- 方法2:构建额外的“类批”维度,不同层之间的计算沿着该维度是独立的;这种独立的维度颗粒越细,内存效率越高,但也会牺牲性能(和方法1差不多,只不过一个是空间上分割,一个是时间上)
推理细节:
- 控制随机种子训练五个不同的模型,有些有模板,有些没有,以鼓励预测的多样性
- 推断五个经过训练的模型,并使用预测的置信度得分来选择每个目标的最佳模型
- 集成模型运行时间:256 个残基-4.8 分钟、384 个残基-9.2 分钟和 2500 个残基-18 小时
- 单个模型运行时间:256 个残基-0.6 分钟、384 个残基-1.1 分钟和 2500 个残基-2.1 小时
- 具有 16 GB 内存的 V100,可运行单个模型预测多达约 1,300 个残基的蛋白质结构
2.3.2 模型评价
全局距离测试(Global Distance Test,GDT)是一种广泛用于评估蛋白质结构预测模型的指标。GDT描述了实际蛋白质结构(目标结构)和预测模型之间的一致性
- 对于目标结构和预测模型,计算所有对应氨基酸残基(Cα原子)之间的距离
- 给定距离阈值,GDT描述了在距离在阈值范围内的氨基酸残基的比例
类似于GDT,IDDT-Cα (Independent Distance Difference Test)也可用于计算了实际蛋白质结构(目标结构)和预测模型之间的一致性
- IDDT会先分别计算目标结构和预测模型中不同残基上的Cα原子间距离
- 当距离在目标结构和预测模型中的差异在指定阈值范围内,则判断为一致
- 此外,lDDT还会通过参考值评估蛋白质的化学结构质量/物理合理性
- pLDDT是模型对IDDT-Cα分数的置信度预测(结果离散化/直方图分布)
模板建模评分(template modeling score,TM-score)是衡量两种蛋白质结构之间相似性的指标
- TM-score介于0~1之间,1表示完美匹配;>0.5表示结构大致相同;<0.2表示结构不相关
- TM-score会先进行残基的对齐,再根据归一化的距离尺度评估两种蛋白质结构之间的距离
- 类似于pLDDT,模型也可以输出基于TM-score的置信度预测(pTM)
不同数据集下,Evoformer块与模型性能表现(GDT)间的关系
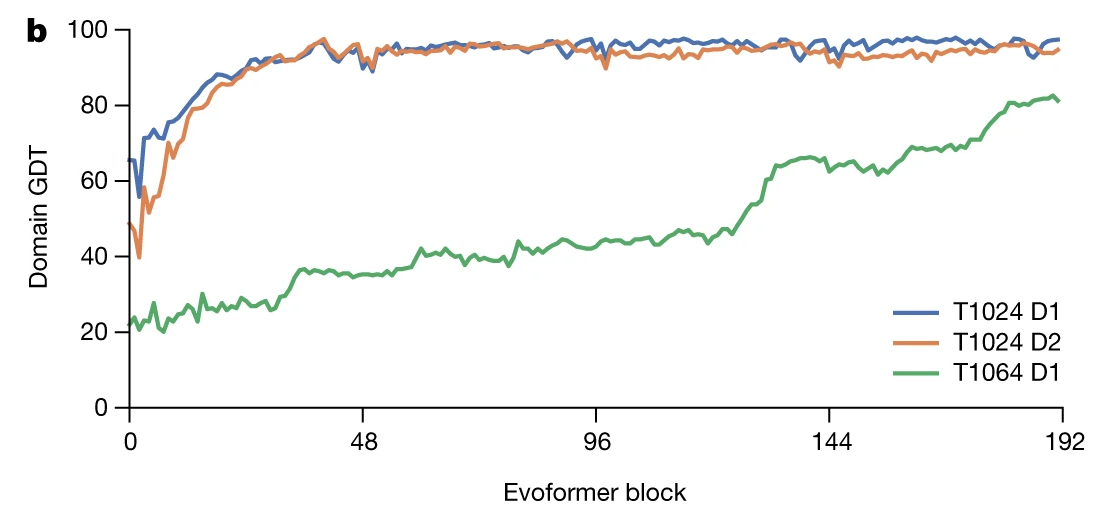
距离误差分布直方图 & 主链评分与侧链评分的相关性分析:
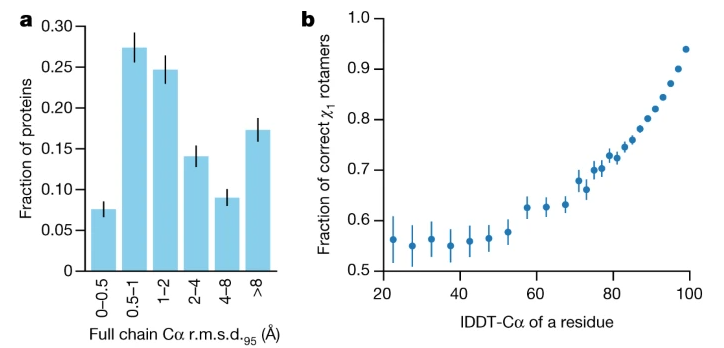
- 图(a)描述了主链(骨干框架)上残基的距离/误差(均方根)分布直方图
- 图(b)描述了主链评分(IDDT-Cα)与侧链准确率的相关性(很强的正相关)
Cα.r.m.s.d.95是指按照误差从低到高排序的95分位数(不考虑部分真实建模错误);AlphaFold 结构的中位骨架精度 Cα.r.m.s.d.95 为 0.96 Å(95% 置信区间 = 0.85~1.16 Å)
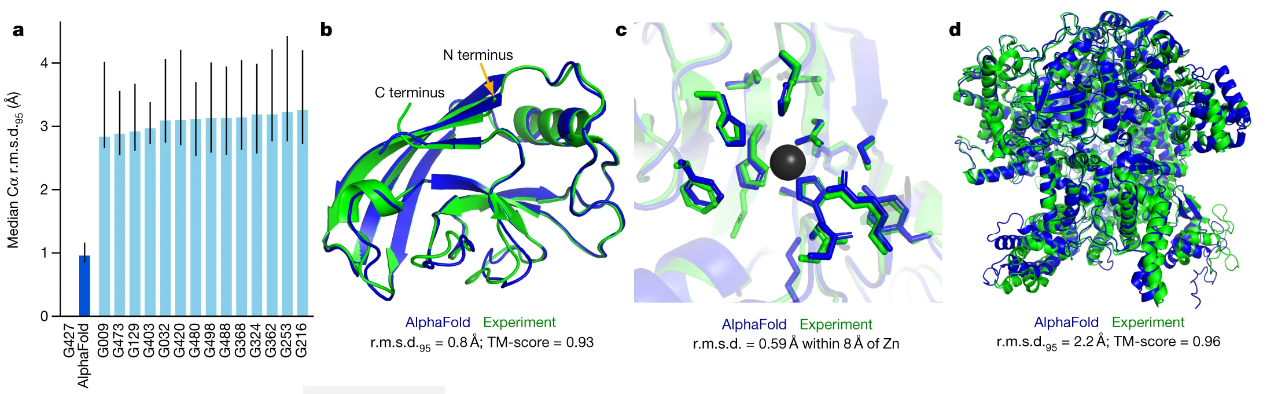
- 图(a)AlphaFold模型的Cα.r.m.s.d.95精度和其他模型的对比(遥遥领先)
- 其他几个图是具体蛋白质结构的预测与实际实验的对比(绿色/真实;蓝色/预测)
- 图(c)中模型预测预留了锌离子的结合位点;图(d)是一个2,180个残基的单链
IDDT-Cα真实值与预测置信度pTM的中位数之间的相关性(基本一致):
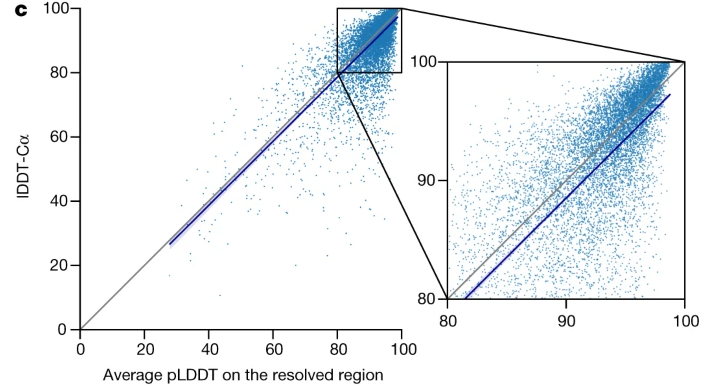
TM-score真实值与预测置信度pLTM的中位数之间的相关性(pLTM略保守):
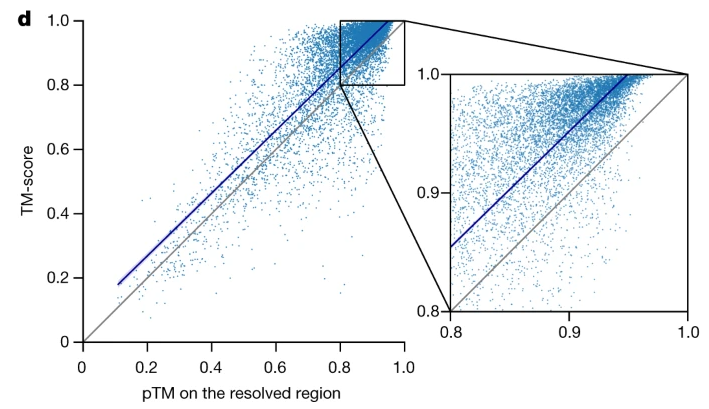
2.3.3 消融实验
不同序列数据源的影响:
- 删除 BFD 使平均准确度降低了 0.4 GDT
- 删除 Mgnify 使平均准确度降低了 0.7 GDT
- 删除两者则使平均准确度降低了 6.1 GDT
其他关键技术的相关消融实验:
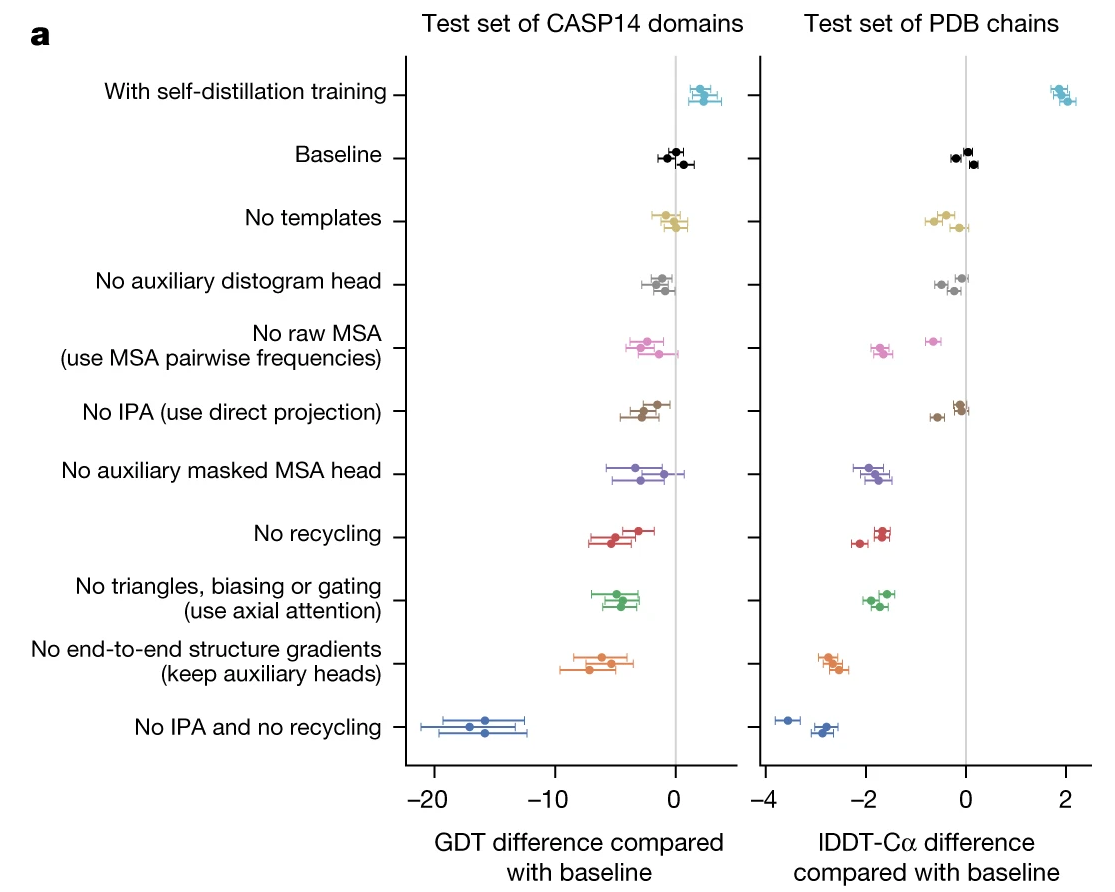
- 自蒸馏(self-distillation)训练的加入较大地改善模型性能,尤其是IDDT-Cα评分
- No templates:删除模板的扭转角特征;No auxiliary distogram head:去除预测直方图的预测
- No raw MSA:去除额外的MSA特征处理流程,直接使用MSA的一阶、二阶统计信息
- No IPA:去除IPA模块,改为直接投影;No recycling:去除回收迭代
- No auxiliary masked MSA head:删除与MSA遮蔽相关的损失项,但保留遮蔽操作
- No triangles, biasing, or gating:将带门控的三角更新改为普通的自注意力
- No end-to-end structrure gredients:结构模块的损失不会反向传递到Evoformer
- 当 No IPA 和 No recycling 同时消融时,模型性能下降明显
不同的消融对 MSA 深度的依赖性非常不均匀。一些消融(例如“No masked MSA head”)主要影响浅层 MSA,而其他消融(例如“No recycling”)则对所有 MSA 深度都有影响
No IPA 和 No recycling直接可能存在交互作用,因为单独的No IPA 消融对模型的影响很有限(这一点也比较让研究者惊讶,网络的旋转位移不变性没那么重要?)
2.3.4 其他分析
MSA深度分析 & 蛋白质同聚物示例:
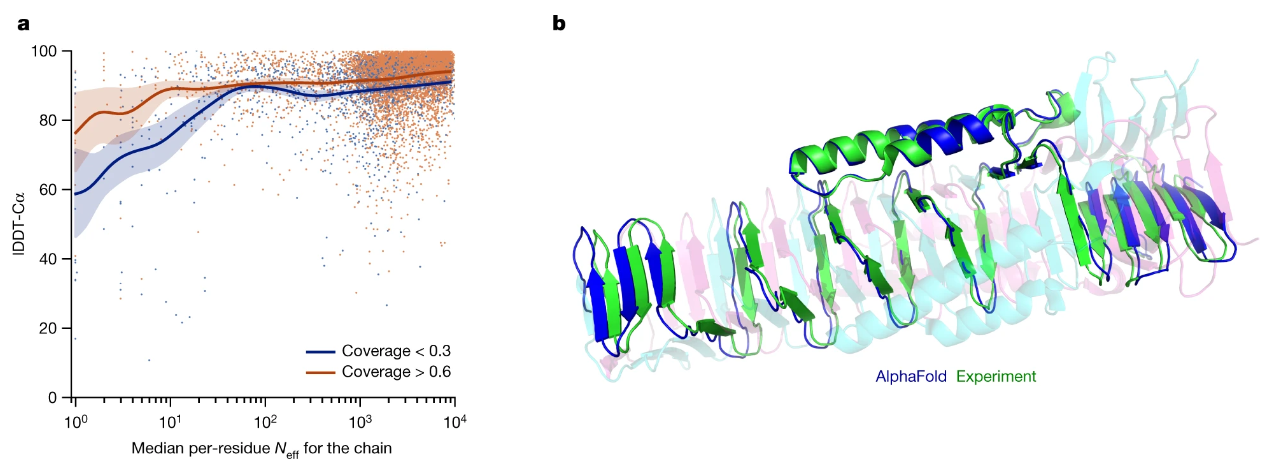
- 图(a)中展示了不同深度的MSA曲线对应的精度(IDDT)变化,其中蓝线表示同一性小于30%的MSA,橙线表示同一性大于60%的MSA;上图显示,当MSA深度(序列数)在30以下时,模型准确率会有大幅下滑;同一性低的MSA对应的模型性能表现会相对更差
- 图(b)中展示了一个特殊示例(预测的还行):交织的同源三聚体(PDB 6SK0)蛋白质
注释:$N_{eff}$表示MSA中合理序列的数量,具体细节可参考论文
局限性分析(部分参考源):
- 硬件需求高;不适用于过大的蛋白质或多蛋白质复合体
- 对已有数据可能存在过拟合(第三方测试显示,已知结构准确率远高于未知结构)
- 蛋白质结构拥有非常动态的结构,而目前的AlphaFold2 只能预测静态解
- 可能存在过度工程化(部分技巧的作用存疑);部分超参没有充分测试
- 没有揭示蛋白质折叠的机制或规则,以考虑解决蛋白质折叠问题
- 该模型对于固有无序蛋白质是不可靠的,但可以通过低置信度分数传达了信息
2.4 后记
与第1代的对比:
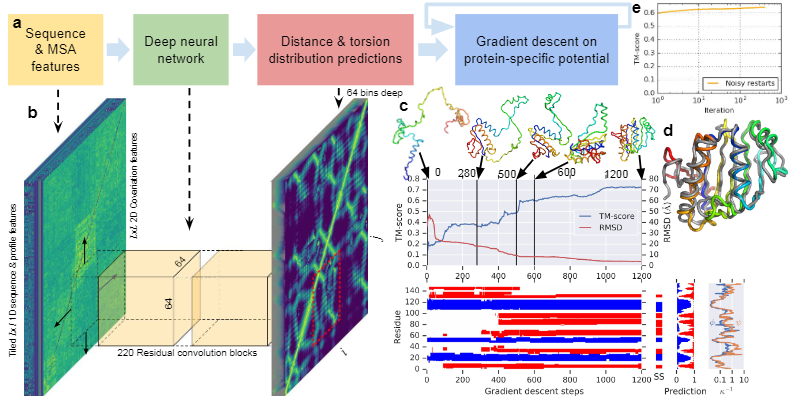
- AlphaFold 1的输入仅考虑了基本的MSA特征;中间的模型块使用的是残差网络
- AlphaFold 1的输出为预测的距离分布、夹角分布;没有单独的原子3D坐标转化
主流评价:
- 98.5%的人类蛋白质被AlphaFold破译,极大地扩展了蛋白结构覆盖率
- 数据的免费开放将进一步的激发基础科学、药物研发、合成生物学设计方面的未来发展
- 人类在认识自然界的科学探索征程中的里程碑事件,大大改进人类对于生命过程的理解
- 2023年的拉斯克(“诺奖风向标”)基础医学研究奖授予给两位AlphaFold主要研发者
其他思考:
- 是否还存在更多的领域可以实现AI+的急速突破
- AlphaFold2 的背后是否还存在更多值得挖掘的东西(可解释性)
- 每一个能被AI突破的领域背后都有无数人无私开源的数据支撑
2024-05 AlphaFold3 问世:
- 预测精度和准确率得到显著提升
- 但代码和模型暂未开源,但有一个免费研究平台「 AlphaFold Server 」
- 闭源行为遭到了多位科学家的公开指责,也有第三方开始进行开源实现
2024-10 《Cell》发表文章:研究者使用 AlphaFold 揭露了精子和卵子结合的分子机制
2024-11-11 AlphaFold3 开源