中介效应分析
发表评论
2405 views

1 基本介绍

中介效应（mediation effect）分析能解释自变量 X 对因变量 Y 的影响是如何通过中介变量(mediator) M实现的，是多变量研究的重要统计方法。

中介效应 VS 间接效应(indirect effect)

  • 在只有一个中介变量的模型中，二者是等价的
  • 当中介变量大于1时，间接效应可以是某特定中介变量的中介效应，也可以是某几个或所有中介效应的和

中介效应 VS “遮掩效应” (suppression effects)

  • 当自变量 X 对因变量 Y 的影响显著时，使用中介效应分析X是如何影响Y的
  • 当自变量 X 对因变量 Y 的影响不显著时，使用遮掩效应分析X为何不影响Y的

2 简单中介效应

假设变量都是连续并且已经标准化(回归方程中没有截距项)，则简单中介效应模型的分析就是拟合得到如下线性回归方程： $$ \begin{equation} \left\{ \begin{gathered} Y&=cX+\epsilon_1 \ \ \ \ \ \ (1) \ \\ M&=aX+\epsilon_2 \ \ \ \ \ \ (2) \ \\ Y&=c'X+bM+\epsilon_3 \ \ \ \ \ \ (3) \end{gathered} \right. \end{equation} $$

  • 其中回归系数$c$表示自变量 X 对因变量 Y 的效应;
  • 回归系数$a$为自变量 X 对中介变量 M 的效应
  • 回归系数$b$表示控制了 X 的影响后 M 对 Y 的效应
  • 回归系数$c'$表示控制了 M 的影响后 X 对 Y的效应
  • $\epsilon$表示残差, 假设残差服从正态分布且相互独立

上式将(3)代入(2)，整理可得： $$Y=(c'+ab)X+\epsilon_2 b + \epsilon_2$$

  • 其中$ab$为自变量 X 对因变量 Y 的中介效应(mediation effect)
  • $c'$为 X 对 Y 的直接效应(directeffect)，$c'+ab$为 X 对 Y 的总效应(total effect)
  • 当回归系数$c'$不显著时，自变量 X 对因变量 Y 是完全中介效应

3 中介效应检验

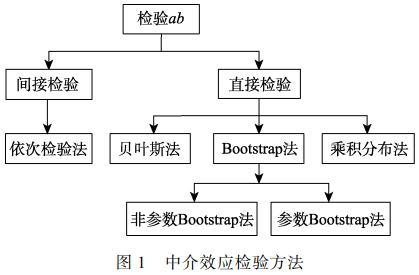
依次检验法，又称联合显著法：

  • 基本思路：依次检验方程(2)的系数$a$和方程(3)的系数$b$，两个系数都显著（对应的备择假设是$H1:a \neq 0 且b \neq 0$）时推得中介效应$ab$显著（对应的备择假设是$H1:ab \neq 0$）
  • 需要注意的一个细节是，一般假设检验显著时对应的$I$型错误率是$0.05$，而联合显著法检验时对应的$I$型错误率是$1-0.95^2=0.0975$

贝叶斯法，又称为马尔科夫链蒙特卡罗法 (Markov Chain Monte Carlo, MCMC)：

  • 基本思路：它将参数看成是随机变量, 将参数的先验分布和观测数据整合在一起, 通过MCMC法得到参数的后验分布和区间估计, 如果区间估计不包含0, 就表示中介效应显著
  • 贝叶斯法的关键步骤是为模型参数选择合适的先验分布。当样本量小或抽样方差大时, 合适的先验信息能有效改善参数的估计

Bootstrap 法：

  • 非参数法与参数法主要是重复抽样的对象不同：非参数法的抽样过程依赖于样本数据，当参数已知（估计值和标准误差）时的便可以使用参数法，即借助蒙特卡罗法(MC)进行模拟抽样
  • 基本思路： 通过不断抽取Bootstrap 样本并计算 a 和 b 的估计值, 得到 ab 的Bootstrap 区间估计, 如果区间估计不包含 0, 则中介效应显著

乘积分布法：

  • 基本思路：乘积分布法默认 ab 的分布是两个正态变量的乘积分布, 根据乘积分布得到 ab 的区间估计, 如果区间估计不包含 0, 则中介效应显著
  • 乘积分布法只需要提供 a 和 b的估计值及其标准误差即可, 不需要原始数据

不同检验方法的选择：

  • Bootstrap 法是应用最为广泛的直接检验系数乘积的方法
  • 一般推荐先使用依次检验法，当依次检验法不显著时再考虑Bootstrap 法
  • 如果要报告中介 效应的置信区间, 使用 Bootstrap 法较好
  • 如果有合适 的先验信息, 也可使用贝叶斯法

其他不推荐的中介效应检验方法

  1. 系数差异检验法，检验的原假设为$H_0:c-c'=0$，此方法的$I$型错误率有时会很高，所以已被淘汰
  2. 直接检验法之Sobel检验，基于正态假设检验$ab$的分布，在系数满足正态分布的情况下，系数的乘积也不一定是正态的，所以此方法局限性比较大，现在很少有人用了

4 中介效应的效应量

效应量是对中介效应的量化

常见的几种中介效应的效应量如下所示：

  1. 中介效应与总效应之比

$$P_M=ab/c$$

  • 在$ab$和$c$符号一致时推荐使用，适用于大样本（>500）的情况
  1. 中介效应与直接效应之比

$$R_M=ab/c'$$

  • 相比$PM$波动性更大，稳定所需的样本量也更多（>5000）
  1. 中介效应与可能的最大中介效应之比

$$k^2=ab/ab_{max}$$

  • 最大中介效应计算主要根据系数$a$和$b$可能的变化区间计算出$ab$可能的变化区间（计算已集成在了R语言的MBESS包中），此方法是对$R_M$的改进
  • $k^2$的缺点是不具备单调性，并且分母的计算方式不被广泛认可
  1. 从方差解释率的角度提出的效果量

$$R^2_{med}=r^2_{MY}-(R^2_{Y,MX}-r^2_{XY})$$

  • 其中$r^2_{MY}$是因变量Y与中介变量M的相关系数，表示Y可以被M解释的部分
  • $R^2_{Y,MX}$是回归方程(3)的拟合优度（决定系数/测定系数），表示Y可以被X和M共同解释的部分
  • $r^2_{XY}$是因变量Y与自变量X的相关系数，表示Y可以被X解释的部分
  • 所以$R^2_{med}$表示 Y 的方差只能被 X 和 M 共同解释而不能被 X 或 M 独立解释的部分
  • $R^2_{med}$的缺点是不具备单调性，并且可能存在负值的情况
  1. $v$：对$R^2_{med}$的改进

$$v=(r_{MY}-ac')^2-(R^2_{Y,MX}-r^2_{XY})$$

  • 其实就是把$R^2_{med}$中的$R_{Y,MX}$替换为了$R_{Y,MX}-ac'$
  • 具备了单调性，但可解释性明显低于$P_M$

5 中介效应分析示例

以R语言为例，分析X（成绩）与 Y（幸福）之间的关系，并考虑中介因素 M（自尊）

# 加载模拟数据
myData <- read.csv('http://static.lib.virginia.edu/statlab/materials/data/mediationData.csv')
model.0 <- lm(Y ~ X, myData) # 拟合方程（1）
summary(model.0)
# Coefficients:
#             Estimate Std. Error t value Pr(>|t|)    
# (Intercept)   2.8572     0.6932   4.122 7.88e-05 ***
# X             0.3961     0.1112   3.564 0.000567 ***

### b1 = 0.3961, p < .001  # significant!

model.M <- lm(M ~ X, myData) # 拟合方程（2）
summary(model.M)
# Coefficients:
#             Estimate Std. Error t value Pr(>|t|)    
# (Intercept)  1.49952    0.58920   2.545   0.0125 *  
# X            0.56102    0.09448   5.938 4.39e-08 ***

model.Y <- lm(Y ~ X + M, myData) # 拟合方程（3）
summary(model.Y)
# Coefficients:
#             Estimate Std. Error t value Pr(>|t|)    
# (Intercept)   1.9043     0.6055   3.145   0.0022 ** 
# X             0.0396     0.1096   0.361   0.7187    
# M             0.6355     0.1005   6.321 7.92e-09 ***

### b4 = 0.0396, p = 0.719   # the effect of X on Y disappeared!
### b3 = 0.6355, p < 0.001

library(mediation)
med.out <- mediate(model.M, model.Y, treat='X', mediator='M',
                   boot=TRUE, sims=500) # 效应分析
summary(med.out)
#                Estimate 95% CI Lower 95% CI Upper p-value
# ACME             0.3565       0.2155       0.5291    0.00
# ADE              0.0396      -0.1761       0.2598    0.66
# Total Effect     0.3961       0.1563       0.5794    0.00
# Prop. Mediated   0.9000       0.5254       1.8820    0.00

### ACME表示中介效应，ADE表示直接效应，Total Effect表示总效应
### ACME = 0.3565, 95% CI [0.2155, 0.5291]  # 中介效应显著
### 中介效应占比 Prop. Mediated = ACME / Total Effect 
### 结论：“成绩”和“幸福感”之间主要是间接效应，中介变量为“自尊”

# 以上流程只是为了方便理解，实际使用可简化为如下四行：
model.M <- lm(M ~ X, myData)
model.Y <- lm(Y ~ X + M, myData)
med.out <- mediate(model.M, model.Y, treat='X', mediator='M',
                   boot=TRUE, sims=100)
summary(med.out)
# 可视化效应分析
plot(med.out) 
# 敏感性分析
sens.out <- medsens(med.out, rho.by = 0.1, effect.type = "indirect", sims = 100) summary(sens.out)
#     Rho  ACME     95% CI Lower  95% CI Upper  R^2_M*R^2_Y* R^2_M~R^2_Y~
#[1,] 0.4  0.1141      -0.0016       0.2297         0.16       0.0738
#[2,] 0.5  0.0358      -0.0742       0.1459         0.25       0.1153
#[3,] 0.6 -0.0601      -0.1713       0.0511         0.36       0.1660
### Rho为灵敏度参数，Rho=0表示没有混杂效应
### Rho值越大表示混杂效应越强，此时对应的中介效应结果越可靠
### 上述结果给出了不同Rho下的中介效应的区间与拟合优度R^2
par(mfrow = c(1,2)) # 敏感性分析可视化
plot(sens.out, sens.par = "rho", main = "Anxiety", ylim = c(-0.2, 0.2))
plot(sens.out, sens.par = "R2", r.type = "total", sign.prod = "positive")

流程小结：

其他代码实践案例：

6 复杂中介效应模型

带有类别变量的中介效应模型：

  • 自变量属于类别型变量的使用哑变量处理
  • 因变量或中介变量属于类别型，线性回归改为逻辑回归
  • 逻辑回归系数注意先进行标准化处理（如$a_{new}=a/SE(a)$），再计算效果量

使用纵向数据的中介效应模型：

  • 此类模型主要用于考察时间变化、个体变化、多水平模型整合等情况
  • 方法一般为多层线性模型、潜变量增长模型、交叉滞后面板、多层自回归

多重中介效应模型：通过多个中介变量更清晰地解释自变量对因变量的效应

多层中介效应模型：适用于多层（嵌套）非独立数据，如学生信息嵌套于班级信息

有调节的中介模型：受调节变量Z的影响的中介过程，即中介量会随 Z 的不同取值而变化

有中介的调节模型：中介过程受调节变量Z的影响，并且调节效应（至少部分地）通过中介变量M对因变量Y起作用（即限定了调节变量Z的影响是通过中介变量M传达的）

参考

2022年论文-国内中介效应的方法学研究
Introduction to Mediation Analysis - R

往年同期文章