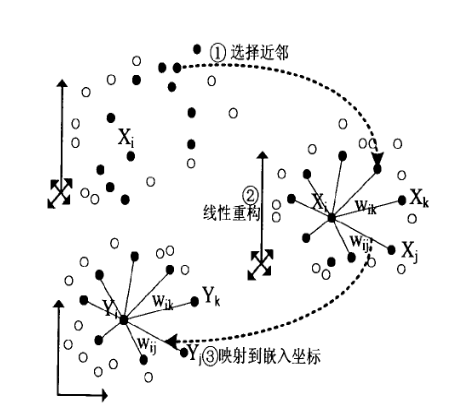
UMAP 算法
- 全称为均匀流形近似与投影,Uniform Manifold Approximation and Projection
- UMAP 是一种基于黎曼几何和代数拓扑理论框架的数据降维与可视化算法
- UMAP 能同时捕捉数据的局部和全局结构,可拓展性强,对嵌入维度没有限制
- MAP 不具备PCA 或因子分析等线性技术可以提供的解释性(因子载荷)
UMAP 定义的概念解释与补充:
- Uniform 均匀假设:通过空间的扭曲,对样本稀疏/密集的位置进行收缩或拉伸
- Manifold 流形:一种拓扑空间,每个点的附近局部类似于欧几里得空间
- Approximation 近似:用一组有限的样本组
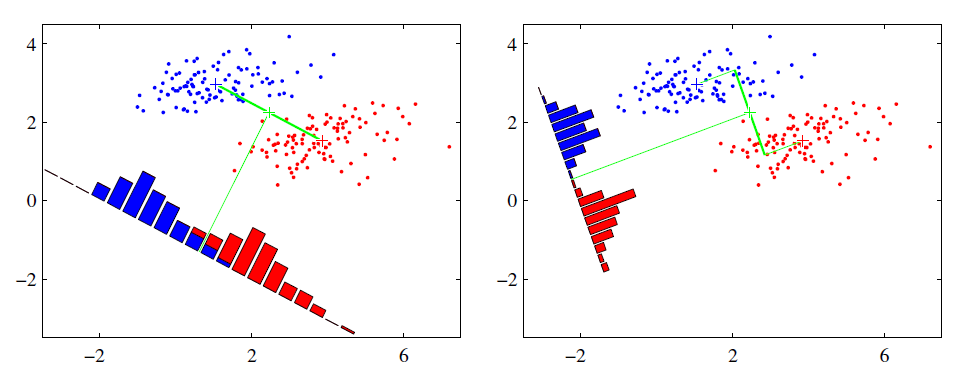
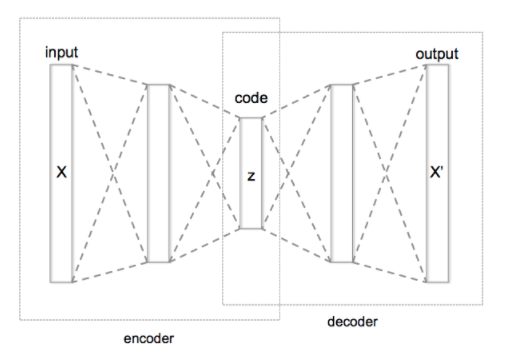 (图源:维基百科-自编码器)
(图源:维基百科-自编码器)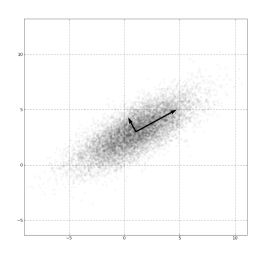 (图源:维基百科-主成分分析)
(图源:维基百科-主成分分析)