中文标题：TPE：基于贝叶斯的超参优化算法改进
英文标题：Algorithms for hyper-parameter optimization
发布平台：NIPS
Advances in neural information processing systems
发布日期：2011-01-01
引用量（非实时）：4544
DOI：缺失
作者：James Bergstra, Rémi Bardenet, Yoshua Bengio, Balázs Kégl
关键字： #贝叶斯 #超参优化 #SMBO #高斯过程 #TPE
文章类型：conferencePaper
品读时间：2023-03-14 18:04
1 文章萃取
1.1 核心观点
- 本文首先针对贝叶斯优化提出了一个通用的算法架构SMBO，并以EI最大化作为采集策略、高斯回归过程GP作为代理模型进行框架的算法示例。之后本文提出一个全新的自动调参算法——TPE算法。TPE算法在普通贝叶斯优化（GP-BO）的基础上对EI采集策略进行调整优化，使用树结构存储超参空间的同时借助Parzen估计器进行概率密度估计。最后论文使用DBN进行超参数优化，通过多次重复实验分析验证了SMBO框架和TPE算法的效果
1.2 综合评价
- 本文提出的TPE算法收敛速度快，调参结果好，是目前自动调参的主流算法
- 本文为会议论文，内容丰富但细节不足，可能对基础薄弱的人群不太友好
- 本人结合多篇论文和网络参考，对本文内容进行了扩充与丰富（不推荐硬啃原论文）
1.3 主观评分：⭐⭐⭐⭐
2 精读笔记
2.1 背景介绍
超参自动优化的必要性
- 传统神经网络模型（DBN，SDAE，CNN等）一般会有10~50个超参数
- 过多的可调参数严重干扰了结果的复现和模型的持续优化
- 超参数优化应该被视为建模学习过程中的一个正式的外部循环
- 针对过往研究的分析表明，机器学习中的超参数优化应考虑分配更多的计算资源
2.2 SMBO框架
基于模型的序列全局优化（Sequential Model-Based Optimization，SMBO）是一种常见的函数优化方法，SMBO常使用高斯过程模型对目标函数进行建模，并使用最优化算法在模型上进行采样来寻找最优解。
- 无需计算梯度，适合目标函数难以解析或计算成本高的场景
- 可处理连续型、类别型变量、条件变量；容易实现并行计算
SMBO的算法实现：
- 其中$x$是一种超参组合，$f$表示评价函数（又称适应度函数，即Fitness Function）
- $M_t$表示迭代到第$t$次的概率分布模型，由于评价函数一般计算成本较高，因此SMBO常采用高斯过程构建评价函数的概率分布模型。$M_t$被称为代理函数（Surrogate Function，又称响应面，即response surface），能实现代价函数的快速近似计算
- $T$表示最大迭代次数，$H$是一个存储超参组合和评价信息的集合
- $S$是一种最优化算法，SMBO中常用的最优化算法是贝叶斯优化或遗传算法
在本文中，默认将误差/损失函数作为评价函数，因此$f$越小越好
SMBO的算法理解
- 在第$t$次迭代过程中，会记录当前选择的超参组合$x^{\ast}$和对应的评价结果$f(x^{\ast})$，并存入集合$H$
- 集合$H$更新后，SMBO会根据其中的历史信息构建代理函数，即评价函数的概率分布模型$M_t$
- 而新的超参组合$x^{\ast}$则是通过最优化算法得到的，以贝叶斯优化为例，此时算法会借助代理函数得到不同超参取值下的预估评价值$y$和对应的概率$p(y|x)$，之后以预期提升（EI，Expected Improvement ）最大化原则寻找$x^{\ast}$，EI的公式如下所示：
$$EI_{y^{\ast}}(x):=\int_{-\infty}^{+\infty}max(y^{\ast}-y,0)p(y|x)dy=\int_{-\infty}^{y^{\ast}}(y^{\ast}-y)p(y|x)dy \tag{1}$$
- 上式中的$y^{\ast}$是一个需要指定的评价值阈值（可选择某一个baseline对应的评价值或历史记录中最好的一次评价值）
- 而$EI_{y^{\ast}}(x)$的含义就是当超参组合$x$确定的情况下，其对应的是预估评价值$y$相对于阈值$y^{\ast}$的改善量（因为$y$越小越好，所以就是下降量），而$x^{\ast}$可由下式得到：
$$x^{\ast}=argmax_xEI_{y^{\ast}}(x)$$
扩展思考：Exploitation VS Exploration
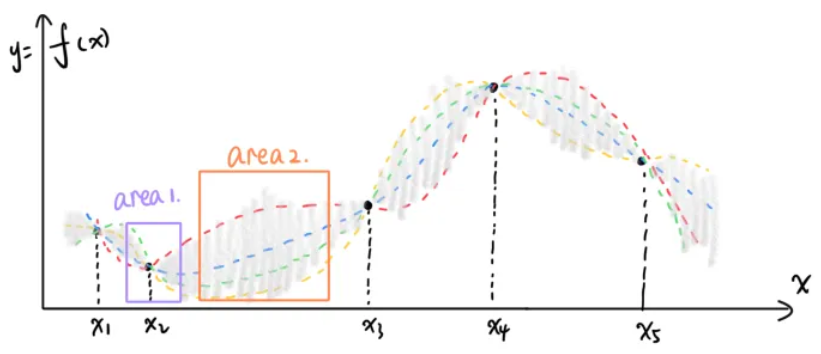
- Exploitation：已探索的最优点附近很有可能存在其他更优点，对应上图中的area 1
- Exploration：未知信息多（确定性小/方差大）的区域可能也是值得探索的，对应上图中的area 2
- EI最大化原在Exploitation和Exploration直接取得了较好的平衡，偏好于选择均值小的、方差大的区域
- 除了EI策略外，新超参组合的选择还有很多种策略，具体可参考贝叶斯优化
2.3 高斯过程GP
高斯过程（Gaussian Processes，简称GP），一种简单的分布拟合方法，常用于损失函数的建模
对于高斯过程感兴趣的读者可参阅高斯过程回归，此处不再赘述
2.4 TPE算法
TPE是树结构Parzen估计器（tree-structured Parzen estimator）的简称
相比于普通贝叶斯优化，TPE算法主要有两处改进
- TPE算法针对EI策略进行优化，构建了两个存在差异的条件分布（一好一坏）用来指导采集下一轮迭代的超参组合，让采集策略的结果尽可能接近好的那部分条件分布而远离差的那部分条件分布
- TPE算法使用树结构存储所需要搜索的参数空间，同时更换代理模型方法（原本是高斯回归过程GPR）为parzen-window密度估计器：把每个节点定义为具有指定均值（超参值）和标准偏差的高斯分布，最终的代理输出是所有节点分布堆叠在一起并归一化后的结果
使用树结构的合理性：首先，TPE默认假设不同超参之间是独立的；但很多超参之间是存在约束关系的，比如对于神经网络模型，只有先确定了层数才能确定每一层的超参，对于多模型选择的超参，只有确定了使用SVM才需要考虑核函数的选择；这种层级关系约束的情况使得超参空间天然得适合使用树结构表示
2.4.1 EI策略优化
为了便于EI优化，先使用贝叶斯定理对上文的EI公式进行调整：
$$EI_{y^{\ast}}(x)=\int_{-\infty}^{y^{\ast}}(y^{\ast}-y)p(y|x)dy=\int_{-\infty}^{y^{\ast}}(y^{\ast}-y)\frac{p(x|y)p(y)}{p(x)}dy \tag{2}$$
调整后，就可以很方便地使用超参$\gamma$对$p(x|y)$进行拆分：
$$\begin{equation}
p(x|y) = \left\{
\begin{array}{rl}
l(x) & \mbox{if } y< y^{\ast} \\
g(x) & \mbox{if } y> y^{\ast} \\
\end{array} \right.
\end{equation}$$
- 上式中$y^{\ast}$为$y$的分位数，具体的分位数等级由超参$\gamma$（常见取值为0.15或0.25）确定
- 此处将$y^{\ast}$作为目标值阈值，将$p(x|y)$拆分为低于阈值的条件分布$l(x)$和高于阈值的条件分布$g(x)$
为了方便EI公式的化简，此处还需要先推导$p(x)$与$p(x|y)$的关系，即用$l(x)$和$g(x)$替代$p(x)$： $$p(x)=\int_Rp(x|y)p(y)dy=\int_{-\infty}^{y^{\ast}}l(x)p(y)dy+\int_{y^{\ast}}^{+\infty}g(x)p(y)dy=\gamma l(x)+(1-\gamma)g(x)$$ 将上式带入调整后的EI公式$(2)$，可得： $$\begin{align} EI_{y^{\ast}}(x) & =\int_{-\infty}^{y^{\ast}}(y^{\ast}-y)\frac{p(x|y)p(y)}{p(x)}dy \ \\ & =\int_{-\infty}^{y^{\ast}}(y^{\ast}-y)\frac{l(x)p(y)}{\gamma l(x)+(1-\gamma)g(x)}dy \tag{3} \ \\ & =\frac{l(x)}{\gamma l(x)+(1-\gamma)g(x)}\int_{-\infty}^{y^{\ast}}(y^{\ast}-y)p(y)dy \end{align}$$
原论文中的公式推导过程中存在一点细节上的错误，但不影响结论（本文已对此细节进行了修正）
TPE算法将以EI最大化为原则选择下一轮的超参组合。只考虑与$x$有关的部分，可发现$EI_{y^{\ast}}(x) \propto (\gamma +\frac{g(x)}{l(x)}(1-\gamma))^{-1}$，所以在$\gamma$确定的情况下，TPE算法倾向于在$l(x)$（目标值更低的条件分布）中概率更大的$x$，在$g(x)$（目标值偏高的条件分布）在概率更低的$x$
由于本论文假设目标值越低越好（损失/成本），因此$l(x)$可看作好成绩的分布，$g(x)$可看作差成绩的分布
整个TPE的EI采集策略，可用下图来表示：
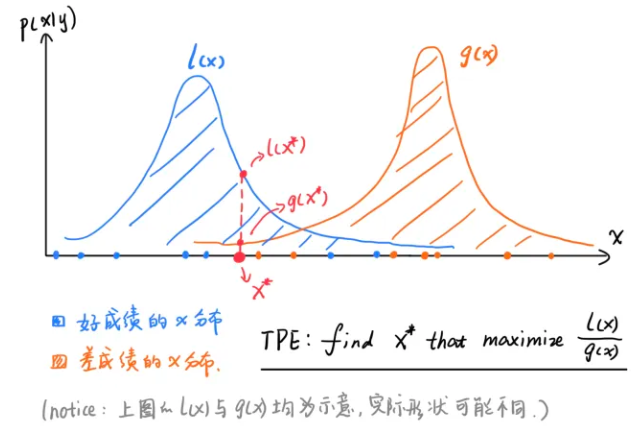（图源：通俗科普文：贝叶斯优化与SMBO、高斯过程回归、TPE）
2.4.2 树结构Parzen估计器
在训练开始前，需要为每个超参初始化一个先验分布（比如均匀分布或高斯分布），并以树结构形式记录参数空间
为方便理解，此处引用了Hyperopt包的超参初始化的代码示例：示例代码参考来源：
import numpy as np
from hyperopt import hp
def uniform_int(name, lower, upper):
# `quniform` returns:round(uniform(low, high) / q) * q
return hp.quniform(name, lower, upper, q=1)
def loguniform_int(name, lower, upper):
# Do not forget to make a logarithm for the lower and upper bounds.
return hp.qloguniform(name, np.log(lower), np.log(upper), q=1)
parameter_space = {
'step': hp.uniform('step', 0.01, 0.5),
'layers': hp.choice('layers', [{
'n_layers': 1,
'n_units_layer': [
uniform_int('n_units_layer_11', 50, 500),
],
}, {
'n_layers': 2,
'n_units_layer': [
uniform_int('n_units_layer_21', 50, 500),
uniform_int('n_units_layer_22', 50, 500),
],
}]),
'act_func_type': hp.choice('act_func_type', [
layers.Relu,
layers.PRelu,
layers.Elu,
layers.Tanh,
layers.Sigmoid
]),
'dropout': hp.uniform('dropout', 0, 0.5),
'batch_size': loguniform_int('batch_size', 16, 512),
}
之后便是关于parzen密度估计器的一些训练细节：
- 在最初的几次迭代过程中，TPE算法会先使用随机搜索等简单方法积攒训练数据，即热身（warn up）
- 对于给定的一种超参组合$x$，其对应着树结构参数空间的多个节点
- 以第$i$个节点为例，需要先找到距离$x_i$最近的$m$个训练集样本，组成$B={(x^{(1)},y^{(1)}),...,(x^{(m)},y^{(m)})}$
- 之后parzen密度估计器会根据样本集合$B$构建一个关于节点$x_i$目标值的核密度估计KDE
- 由于$TPE$算法假设不同参数间是独立的，所以将所有节点的KDE堆叠后便得到了超参组合$x$的KDE
- 因为EI策略优化后只需要考虑$f(x)$和$g(x)$，所以可以简化建模过程，直接对$l(x)=p(x|y,y<y^{\ast})$和$g(x)=p(x|y,y>y^{\ast})$构建核密度估计KDE，并找到$l(x)/g(x)$最大的参数组合作为下一轮迭代的超参组合样本
注意：以上过程描述整合了多份资料的结果和主观推断，可能与原始论文存在细节差异
2.5 实验分析与总结
本文实验中使用了DBN神经网络作为基准模型
不同调参方法的对比：
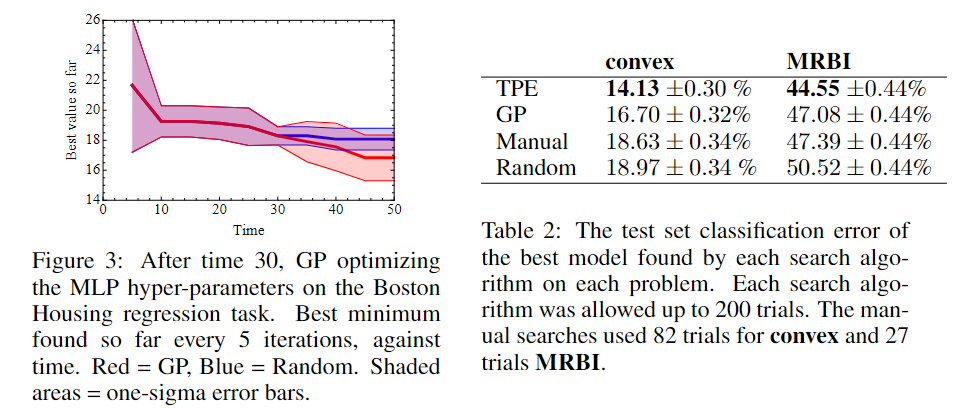
- 左图中，由于TPE算法在前30次迭代时需要热身，所以TPE算法（红）和随机搜索法（蓝）完全重合；而在30次迭代热身后，TPE所采集到的最低目标值就逐渐甩开了随机搜索法，体现了TPE算法快速收敛的能力
- 右图中，作者在两类数据集（convex和MRBI）中分别验证了四种调参方法，每个在被限制为1小时的GPU计算时间的情况下重复多次，最后对比结果表明，TPE算法在两类数据集上均取得了最优的效果
其他分析和总结
- 在超参搜索的实验过程中，GP和TPE算法的效率略低于手动搜索
- GP使用的EI策略相比于TPE更为精准，这可能约束了搜索过程中的启发式探索
- GP和TPE存在陷入局部最优解的可能，在寻找全局最优解方面有时还不如随机搜索法
- 优秀的参数优化方法有助于机器学习结果的传播、发展，或者转移到其他领域