1 点积与行列式
已知三角形面积的计算公式为$S=\frac{1}{2}absin\theta$
则由向量$\vec{A}$和$\vec{B}$组成的平行四边形面积为$S=|\vec{A}||\vec{B}|sin\theta$
设$\vec{A'}$为向量$\vec{A}$逆时针旋转$90°$的结果,$\vec{A'}$与$\vec{B}$的夹角为$\theta'=\frac{\pi}{2}-\theta$
则平行四边形面积为$S=|\vec{A'}||\vec{B}|cos\theta'=\vec{A'}\cdot \vec{B}$
设$\vec{A}=(a_1,a_2)$,$\vec{B}=(b_1,b_2)$,则$\vec{A'}=(-a_2,a_1)$,带入面积公式可得: $$S=<-a_2,a_1>\cdot <b_1,b_2>=det(\vec{A}\cdot \vec{B})= \left| \begin{matrix} a_1 & a_2 \\ b_1 & b_2 \\ \end{matrix} \right| $$ 而这就引出行列式的定义$det(\vec{A}\cdot \vec{B})$以及二阶行列式的几何意义:
二阶行列式绝对值=平行四边形面积
同理可推,三阶行列式的定义为 $$det(\vec{A},\vec{B},\vec{C})=\left| \begin{matrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \\ \end{matrix} \right|$$ 对应的几何意义为:三阶行列式绝对值=平行六面体体积
2 叉积 Cross-product
以三维向量为例,叉积的具体定义如下: $$\vec{A}\times \vec{B}=\left|\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ \end{matrix} \right|=\vec{i}\left|\begin{matrix} a_2 & a_3 \\ b_2 & b_3 \\ \end{matrix} \right|-\vec{j}\left|\begin{matrix} a_1 & a_3 \\ b_1 & b_3 \\ \end{matrix} \right|+\vec{k}\left|\begin{matrix} a_2 & a_3 \\ b_2 & b_3 \\ \end{matrix} \right|$$ 其中$\vec{i},\vec{j},\vec{k}$表示构建三维空间的三个基本单位向量$<1,0,0>,<0,1,0>,<0,0,1>$
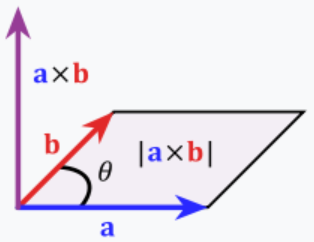
不同于点积,叉积的结果是一个向量,向量的模长等于向量$\vec{A}$和$\vec{B}$构成平行四边形的面积(所以对于三维向量,行列式可用于求体积,而叉积可用于求面积),向量的方向垂直于向量$\vec{A}$和$\vec{B}$构成的平面(需借助右手法则:手掌指向$\vec{A}$,四指折向$\vec{B}$,则拇指指向叉积的方向)
在很多时候,点积也被称为内积,叉积也被称为外积
3 叉积的应用
应用1:三维向量借助点积和叉积求体积
已知三个向量$\vec{A},\vec{B},\vec{C}$,求这三个向量构成的平行六面体的体积$V$ $$V=|\vec{B}\times \vec{C}|(\vec{A\cdot \frac{\vec{B}\times \vec{C}}{|\vec{B}\times \vec{C}|}})=\vec{A}\cdot \vec{B}\times \vec{C}=det(\vec{A},\vec{B},\vec{C})$$ 解析:$|\vec{B}\times \vec{C}|$所得结果为向量$\vec{B}$和$\vec{C}$构成平行四边形的面积,$\frac{\vec{B}\times \vec{C}}{|\vec{B}\times \vec{C}|}$得到的是向量$\vec{B}$和$\vec{C}$构成的平面的法向量,$\vec{A\cdot \frac{\vec{B}\times \vec{C}}{|\vec{B}\times \vec{C}|}}$得到的是向量$\vec{A}$沿着法向量的分量。所以$|\vec{B}\times \vec{C}|(\vec{A\cdot \frac{\vec{B}\times \vec{C}}{|\vec{B}\times \vec{C}|}})$是底面积乘以高的过程。
$\vec{B}\times \vec{C}\neq \vec{C}\times \vec{B}$,虽然模长相同,但是方向相反~
应用2:判断点$P$与点$P_1,P_2,P_3$是否共面
方法1:计算行列式,如果$det(\vec{P_1P},\vec{P_1P_2},\vec{P_1P_3})=0$,说明$V_{PP_1P_2P_3}=0$,则四点共面
方法2:计算法向量,法向量$\vec{N}=\vec{P_1P_2}\times \vec{P_1P_3}$,如果$\vec{N}\perp \vec{{P_1P}}$,则说明四点共面
4 参考
