随机矩阵：元素为随机变量的矩阵，属于概率论与矩阵分析的交叉领域
系综：对符合某种分布的随机变量进行多次取值，得到的矩阵集合
具有统计独立性的实或复矩阵系综，在基变换下分布具有不变性，如果变换是正交的(orthogonal)、酉的(unitary)或辛的(symplectic)，则分别得到高斯正交系综(Gaussian Orthogonal Ensemble，GOE)，高斯酉系综(Gaussian Unitary Ensemble，GUE)或高斯辛系综(Gaussian Symplectic Ensemble，GSE)
此处可先简单理解为，酉变换是实数域的正交变换在复数域上的拓展。对应关系： ① 共轭转置 →对应→ 转置，② Hermite 变换 →对应→ 对称变换，③ Hermite 矩阵 →对应→ 对称矩阵，④ 酉变换 →对应→ 正交变换，⑤ 酉矩阵→对应→ 正交矩阵
至于辛变换则对应着酉变换在更高维度（$V × V → R$）上的拓展。GOE、GUE、GSE中矩阵对应的元素分别为实数、复数和四元数实数项
GOE、GUE和GSE对应的特征值分布如下：
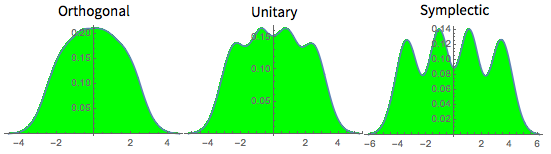（图源：Wolfram 语言随机矩阵示例）
随机矩阵理论 (Random Matrix Theory, RMT) 起源于对量子力学中大量粒子能级的研究，主要研究超大矩阵特征值的统计性质，从而提供对于矩阵性质的理解。
在RMT中用于特征值计算的数值方法主要有两种：
- 通过矩阵的QR分解等方法直接进行数值计算
- 借助PIC（Power iteration clustering）等方法迭代求解
在20世纪50年代后期，E. P. Wigner根据随机矩阵的经验分布来阐述该问题 (Wigner 1955, 1958)，从而开始了对高斯矩阵半圆定律的研究。 自那以后，RMT在现代概率论中便形成了一个活跃的分支。
Wigner矩阵：一个$n\times n$的对称矩阵$M$，矩阵的每一个元素都是随机变量
- 所有非对角元素都是独立同分布的，并且分布的一阶矩为零，二阶矩有限
- 所有对角元素都是独立同分布的，并且分布的一阶矩为零，二阶矩有限
- 非对角元素的分布与对角元素的分布不一定是一致的
Wigner半圆定律：归一化后的Wigner矩阵的谱密度函数图像是一个半圆
- 对$n\times n$的Wigner矩阵$M$进行归一化处理：$X=\frac{1}{\sqrt{n}\sigma}M$
- 归一化后随机矩阵的特征值分布的谱密度函数如下： $$\begin{equation} \sigma(x) = \left\{ \begin{array}{rl} \frac{1}{2\pi}\sqrt{4-x^2} & \mbox{if } |x| \leq 2 \\ 0 & otherwise \\ \end{array} \right.
\end{equation}$$
谱密度函数的含义：任取归一化后的Wigner矩阵的一个特征值，该特征值落在$[x,x+dx]$的概率为$\sigma(x)dx$。谱密度函数曲线是一个以原点为圆心，半径为2的半圆，所以随机矩阵$X$的特征值不能超过区间$[-2,2]$。
此结论只针对无穷维的矩阵成立，实际应用中，多适用于特征维度较高的情况。同时当矩阵特征值分布明显超出区间$[-2,2]$时，说明矩阵不是“真随机“矩阵。
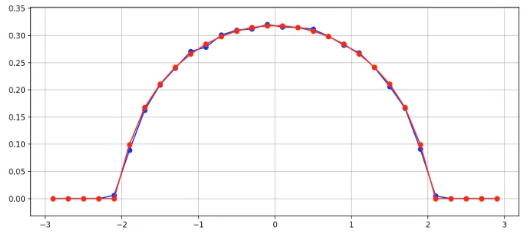（说明：蓝线为模拟的结果，红线为精确解）
RMT理论的主要任务是探究谱分布的极限性质，包括但不限于其他随机分布条件下的谱密度函数、极值特征值、谱间隙、谱统计量、谱分布的收敛性等问题。（内容较多，暂不展开，有需要再考虑深入学习一下）
RMT理论的应用：
- 对高维特征进行筛选/特征选择优化，具体可参考相关文献
- 数据去噪或异常检测：比如针对金融网络进行去噪以更好地验证市场内在规律和趋势，具体可参考相关文献；通过对数据经验谱中异常值对应的特征向量进行分析，对电网异常情况进行检测及定位，具体可参考相关文献。
- 借助RMT理论理解神经网络：比如分析模型初始化和early stopping等行为对模型泛化能力的影响，具体可参考这篇论文；或者刻画不同参数对模型的影响，并将激活函数按照统计信息的能力进行归类，具体可参考这篇文章
进阶阅读材料推荐（我也还没看）：
- 随机矩阵理论(RMT)综述
- 陶哲轩《Topics in Random Matrix Theory》
- 随机矩阵理论及其在大规模机器学习中的应用-廖振宇
参考文献：