1 隐函数微积分
扩展$(x^n)'=nx^{n-1}$为$(x^a)'=ax^{n-1}$
- 其中$a$表示有理数,可以用$\frac{m}{n}$表示
- $m,n \in Z$,即$m$和$n$属于整数集
扩展公式的证明:
- 转换$y=x^{\frac{m}{n}}$为$y^n=x^m$
- 由此可得$\frac{d}{dx}y^n=\frac{d}{dx}x^m=mx^{m-1}$
- 借助链式法则可得$\frac{d}{dy}y^n\frac{dy}{dx}=mx^{m-1}$
- 化简可得$\frac{dy}{dx}=\frac{mx^{m-1}}{ny^{n-1}}$
- 代入$y=x^{\frac{m}{n}}$和$\frac{m}{n}=a$可得$\frac{dy}{dx}=ax^{a-1}$
2 反函数求导
隐函数求导法的一个应用就是求反函数的导数值
下面以$y=arctan(x)$为例,进行演示
前置知识:
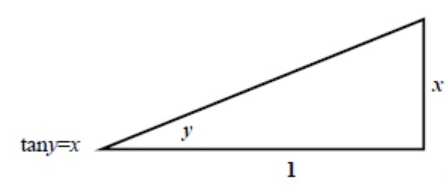
- 如上图所示,$tan(y)=x$可转换为一个直角三角形关系
- 斜边长度为$\sqrt{1+x^2}$,则$cos(y)=\frac{1}{\sqrt{1+x^2}}$
具体导数推导:
- 转换$y=arctan(x)$为$tan(y)=x$
- 两边同时求导可得$\frac{d}{dx}tan(y)=\frac{d}{dx}x=1$
- 借助链式法则可得$\frac{d}{dy}tan(y)\frac{dy}{dx}=1$
- 化简可得$\frac{d}{dx}\frac{sin(y)}{cos(y)}\frac{dy}{dx}=\frac{1}{cos^2(y)}\frac{dy}{dx}=1$
- 最终可得$\frac{dy}{dx}=cos^2(y)=\frac{1}{1+x^2}$
3 参考