1 变化率 rate of change
- 注意:本课前半部分内容为第一节内容未讲完部分。第一节仅描述了导数的几何解释,而变化率则是导数的物理解释。
$$\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\frac{dy}{dx}$$
- $\frac{\Delta y}{\Delta x}$表示的是一种平均值
- $\frac{dy}{dx}$表示的是一种瞬时值
- 随着$\Delta x\to0$,平均值将逼近瞬时值
物理示例参照
- 当q表示电荷量(charge)时,$\frac{dq}{dt}$表示是瞬时电流
- 当s表示路程(distance)时,$\frac{ds}{dt}$表示是瞬时速度
- 当T表示温度(temperature)时,$\frac{dT}{dt}$表示是温度梯度
- 瞬时变化率还可以用于测量灵敏度,应用到诸如GPS等应用中
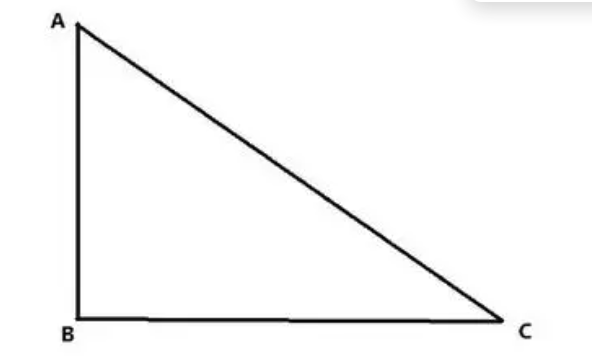
GPS原理(简化版)扩展
- 其中A表示卫星(satellite)位置,C表示待测量的位置
- 距离h=AC可通过无线电/时钟测量得出,但由于电离层干扰存在误差
- B表示卫星精确已知的垂直地表位置,距离L=BC可以通过h推算得出
- 误差$\Delta h$可以通过$\frac{\Delta L}{\Delta h}\approx \frac{dL}{dh}$进行估算
2 极限和连续 limits and continuity
2.1 极限
极限的两种情况
- 简单模式:直接带入极限值即可
$$\lim_{x \to 1}\frac{1}{x}=1$$
- 复杂模式:需要先进行对消运算才能带入
$$\lim_{x \to 0}\frac{x^2+x}{x}=\lim_{x \to 0}x+1=1$$
极限的逼近方向
- 左极限:$\lim_{x \to x^-}f(x)$其中$x < x^-$
- 右极限:$\lim_{x \to x^+}f(x)$其中$x > x^+$
2.2 连续
函数$f(x)$在点$x_0$处连续的定义 $$\lim_{x \to x_0}f(x)=f(x_0)$$
满足定义的三个条件:
- 左右极限存在且相等$\lim_{x \to x^-}f(x)=\lim_{x \to x^+}f(x)$
- 函数$f(x)$在点$x_0$处有定义
- 函数值$f(x_0)$与极限值$\lim_{x \to x_0}f(x)$相等
2.3 四种间断情况
- 跳跃间断(jump discontinuity):左右极限存在且不相等
函数连续性的股票应用
- BobMerton由于其对于股票期权的研究获得了97年诺贝尔经济学奖
- 其模型中非常关注各种股票价格是否左连续或右连续
- 左连续关乎价格的过去信息,右连续关乎价格的未来信息
- 这些信息都应用到了当今对冲基金中的定价函数中
- 可去间断(removable):左右极限存在且相等,但不等于函数值
可去间断举例:$\frac{sin(x)}{x}$
- $\lim_{x \to 0}\frac{sin(x)}{x}=1$
- 函数在$x=0$处无定义
- 无穷间断(infinite)
无穷间断举例:$\frac{1}{x}$
- $\lim_{x \to 0^+}\frac{1}{x}=\infty$
- $\lim_{x \to 0^-}\frac{1}{x}=-\infty$
- 奇函数$\frac{1}{x}$求导后变为了偶函数
- 另类间断(other)
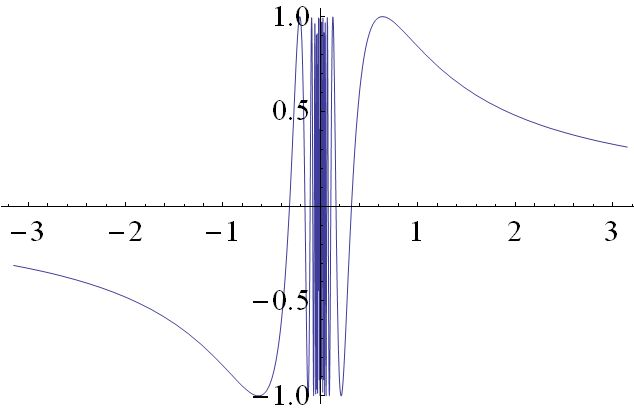
无穷间断举例:$sin(\frac{1}{x})$
- 随着$x \to 0$,$\lim_{x \to 0}f(x)$将剧烈震荡
- 函数在$x=0$处不存在左极限和右极限
2.4 可导必连续
证明: $$\begin{align} \lim_{x \to x_0}f(x)-f(x_0) & =\lim_{x \to x_0}\frac{f(x)-f(x_0)}{x-x_0}(x-x_0) \\ & = \lim_{x \to x_0}{f}'(x)(x-x_0) \\ & = {f}'(x)\times0 \\ & = 0 \end{align} $$ 满足函数$f(x)$在点$x_0$处连续的定义 $$\lim_{x \to x_0}f(x)=f(x_0)$$
参考