高效精准的时序聚类算法K-Shape
发表评论
3963 views

中文标题：高效精准的时序聚类算法K-Shape

英文标题：k-Shape: Efficient and Accurate Clustering of Time Series

发布平台：ACM SIGMOD

Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data

发布日期：2015-05-27

引用量（非实时）：703

DOI：10.1145/2723372.2737793

作者：John Paparrizos, Luis Gravano

关键字： #K-Shape #时间序列 #聚类

文章类型：conferencePaper

品读时间：2022-01-19 17:23

1 文章萃取

1.1 核心观点

本文提出了一种领域独立、高精度、高效的时间序列聚类算法h-Shape。k-Shape以k-means算法为基础，根据时间序列的特殊性，设计了互相关的距离度量算法，以及将质心的寻找转为最优化问题，实现了对时间序列形状的考量，并通过大量数据和算法对比，验证了算法的鲁棒性、准确性和低计算成本。

1.2 综合评价

  • 针对时序聚类做特定优化，包含对时间序列形状的解释性
  • 设计了互相关的距离度量算法，并通过快速傅里叶变换加速运算
  • 将质心的寻找转为（Rayleigh Quotient）瑞利商问题，实现最优化问题的快速计算
  • 最终效果优秀，相比其他算法计算复杂度低两个数量级

1.3 主观评分：⭐⭐⭐⭐⭐

2 精读笔记

2.1 背景知识

时序聚类算法依赖于传统聚类算法，但需要更多适应性的调整，其中最常见的是对距离测度的创新

本文提出的K-Shape算法就是采纳了K-means聚类的思想，不过对于距离度量和质心计算进行了革新，并通过广泛实验进行了验证。

聚类追求的是：簇内样本尽可能相似（同质性最大，homogeneity），簇间样本尽可能不相似（差异性最大，separation），常见的设定目标为距离平方和最小

时序数据寻找质心的过程是一个典型的Steiner’s sequence问题，最终的质心应当满足距离簇内所有样本的距离平方和最小。而对于两段时序，衡量距离的常见方法为欧氏距离（Euclidean Distance，即ED）和动态时间规整（Dynamic Time Warping，即DTW）：

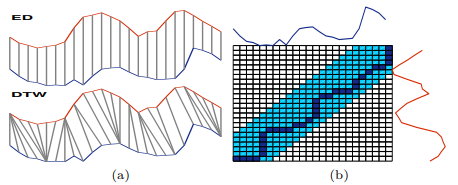
描述时间序列相似度的几种不变性：缩放平移不变性（Scaling and translation invariances）、平移不变性（Shift invariance，可用于局部相似或存在相位差的情况）、均匀缩放不变性（Uniform scaling invariance，常用于时序对齐，比如均匀拉伸短序列或均匀压缩长序列）、闭塞不变性（Occlusion invariance，忽略局部或缺失的子序列）、复杂不变性（Complexity invariance，常用于形状相似但是细节丰富度不同的两个序列）

文中提供的距离测度方法具备伸缩平移不变性

2.2 K-Shape算法介绍

2.2.1 距离测度方法SBD

由于DTW高昂的计算成本，本文主要采用了互相关（Cross Correlation）作为基本的距离测度方法，并通过一系列的优化在一定程度上解决了互相关的性能缺陷。

假设存在两个长度一致的时序，分别为$\vec{x}=(x_1,...,x_m)$和$\vec{y}=(y_1,...,y_m)$

这里之所以设定长度一致，主要是为了简化后续的公式，理解公式后，就发现可以很容易地应用到长度不一致的情况

互相关主要通过在$\vec{y}$上滑动$\vec{x}$并依次进行点乘加和而得（类似于卷积操作）

为了方便处理边缘情况，定义滑动时的$\vec{x}$如下（补零操作）：

$$\begin{equation} \vec{x}_{(s)} = \left\{ \begin{array}{rl} (0_1,...,0_{|s|},x_1,x_2,...,x_{m-s}) & \mbox{if } s \geq 0, \\ (x_{1-s},...,x_{m-1},x_m,0_1,...,0_{|s|}) & \mbox{if } s < 0, \end{array} \right. \end{equation}$$

  • 其中$s\in[-m,m]$，$s\geq 0$对应滑动刚开始时，$\vec{x}$左侧溢出的情况；
  • $s<0$对应滑动快结束时，$\vec{x}$右侧溢出的情况。
  • 最终计算的互相关序列长度为$(2m-1)$，其中第$\omega$个互相关值为$CC_{\omega}$：

$$CC_{\omega}(\vec{x},\vec{y})=R_{\omega-m}(\vec{x},\vec{y})$$ 其中$\omega \in{1,2,...,2m-1}$，而$R_{\omega-m}(\vec{x},\vec{y})$计算方式如下： $$ \begin{equation} R_{k}(\vec{x},\vec{y}) = \left\{ \begin{array}{rl} \Sigma_{l=1}^{m-k}x_{l+k}\cdot y_l& \mbox{if } k \geq 0, \\ R_{-k}(\vec{x},\vec{y}) & \mbox{if } k < 0, \end{array} \right. \end{equation} $$ 其中$k<0$对应$\omega <m$的时候，即$\vec{x}$左溢出的情况，此时的计算转化为$R_{-k}=\Sigma_{l=1}^{m+k}x_{l-k}\times y_l$，也就是向量$(x_{1+|k|},x_{2+|k|},...,x_m)$与向量$(y_1,y_2,...,y_{m-|k|})$的点积和

这里的逻辑看起来复杂，其实就是滑动点乘，只不过将边缘情况考虑进去，而针对边缘情况的补零操作其实也就意味着不计算溢出部分

对互相关结果进行标准化的三种方法 $$ \begin{equation} NCC_{q}(\vec{x},\vec{y}) = \left\{ \begin{array}{rl} \frac{CC_{w}(\vec{x},\vec{y})}{m} & q =b \ (NCC_b), \\ \frac{CC_{w}(\vec{x},\vec{y})}{m-|w|} & q =u \ (NCC_u) \\ \frac{CC_{w}(\vec{x},\vec{y})}{\sqrt{R_0(\vec{x},\vec{x})R_0(\vec{y},\vec{y})}} & q =c \ (NCC_c), \end{array} \right. \end{equation} $$ 前两种标准化方法主要为了消除长度的影响，而第三种方法主要为了消除自相关的应该

以真实数据验证，数据长度均为$1024$，$\omega \in{1,2,...,2048-1}$，则三种方式的结果如下：

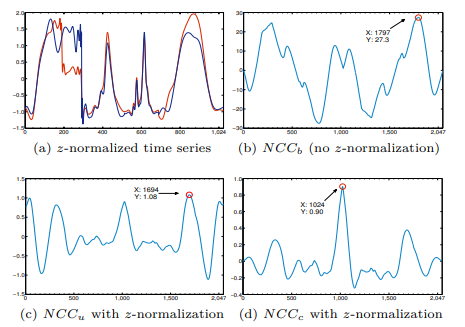
图中红圈对应了匹配度（标准化互相关）最高的时候，也是描述序列间距离的最佳位置

其中子图(d)即表示的本文所采用的标准化方法，对于两侧由于时序长度较短时的异常波动起到了很好的抑制作用，最高点对应的$\omega=m=1024$，也符合直觉判断

而本文的距离（Shape-based distance，简称SBD）计算公式则是根据标准化互相关的简单变形： $$SBD(\vec{x},\vec{y})=1-max_{\omega}(\frac{CC_{w}(\vec{x},\vec{y})}{\sqrt{R_0(\vec{x},\vec{x})R_0(\vec{y},\vec{y})}})$$ 值得一提的是，借助快速傅里叶变换（FFT）可以将距离计算的复杂度从$O(n^2)$降到$O(nlgn)$

具体算法流程如下：

2.2.2 质心计算

传统聚类算法，如K-means都是采用簇内均值作为质心的计算方式，但是这种方式对于时序数据来说，不能够把握住时序的特征，均值方法（实线）与本文方法（虚线）对比如下：

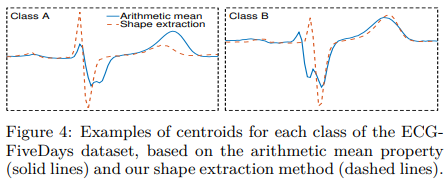
本文方法是建立最优化问题，寻找与第$k$个簇内与所有时序互相关值和最小的时序$\vec{u}_k^{\ast}$：

$$\vec{u}_k^{\ast}=argmax_{\vec{u}_k}\Sigma_{\vec{x_i}\in P_k}(\frac{max_w CC_w(\vec{x_i},\vec{u_k})}{\sqrt{R_0(\vec{x_i},\vec{x_i})\cdot R_0(\vec{u_k},\vec{u_k})}})$$

由于均值方法得到的质心与本文方法得到的质心较为相似，所以考虑采用均值法质心用于时序对齐，计算得到合理的$\omega$，然后省略上公式的部分，可将$\vec{u_k^{\ast}}$的公式更新如下： $$\vec{u}_k^{\ast}=argmax_{\vec{u}_k}\Sigma_{\vec{x_i}\in P_k}(\Sigma_{l\in {[1,m]}}x_{il}\cdot \mu_{kl})^2$$ 公式的向量化表示结果如下： $$\vec{u}_k^{\ast}=argmax_{\vec{u}_k}\Sigma_{\vec{x_i}\in P_k}(\vec{x_i^T}\cdot \vec{u_k})^2=argmax_{\vec{u}_k}\vec{u_k^T}\cdot \Sigma_{\vec{x_i}\in P_k}(\vec{x_i}\cdot \vec{x_i^T} )\vec{u_k}$$ 令$\vec{u}_k=\vec{u}_k\cdot Q$使其中心化，其中$Q=I-\frac{1}{m}O$，$I$是单位矩阵，$O$是全1矩阵

令$S=\Sigma_{\vec{x_i}\in P_k}(\vec{x_i}\cdot \vec{x_i^T} )$简化公式，最后除以$\vec{u}k^T\cdot \vec{u}_k$对$\vec{u}_k$进行归一化，最终公式如下： $$\vec{u}_k^{\ast}=argmax\{\vec{u}_k}\frac{\vec{u}_k^T\cdot Q^T\cdot S \cdot Q \cdot \vec{u}_k}{\vec{u}_k^T\cdot \vec{u}_k}=argmax_{\vec{u}_k}\frac{\vec{u}_k^T\cdot M \cdot \vec{u}_k}{\vec{u}_k^T\cdot \vec{u}_k}$$

最终公式转换为了一个（Rayleigh Quotient）瑞利熵问题，其最大特征值即对应了最优化问题的最大值，最大特征值对应的特征向量对应了本文所需的质心$\vec{u}_k^{\ast}$

具体算法流程如下：

2.2.3 K-shape时序聚类

K-shape聚类方法与K-means方法很像，只不过距离计算方法改为了SBD，质心计算方法也进行了相应调整，具体算法流程如下：

简单来说，就是在迭代中根据SBD将每个时序分配给最相似的簇，然后更新簇的质心，进入下一次迭代，直到最终簇的分布不再变化或者达到最大迭代次数（100）

算法复杂度分析：$n$表示序列个数，$m$表示序列长度，$k$表示簇/类别的个数

  1. 计算SBD距离并分配每个时序给相应簇，其中计算SBD距离的复杂度为$O(mlogm)$，距离计算会重复$n\cdot k$次，所以此过程最终计算复杂度为$O(n\cdot k \cdot m \cdot log(m))$
  2. 计算矩阵$M$的复杂度为$O(n\cdot m^2)$，求解矩阵$M$的特征矩阵的复杂度为$O(k\cdot m^3)$
  3. 最终K-shape算法的计算复杂度为$O(max{n\cdot k \cdot m \cdot log(m), n\cdot m^2, k\cdot m^3})$

2.3 实验评估

最终评估使用48个带标签数据集，不同数据集的序列个数从56到9000+不等，不同数据集的序列长度从24到1882不等，不过同一个数据集的序列长度相同

最终不同距离度量方法的对比如下：

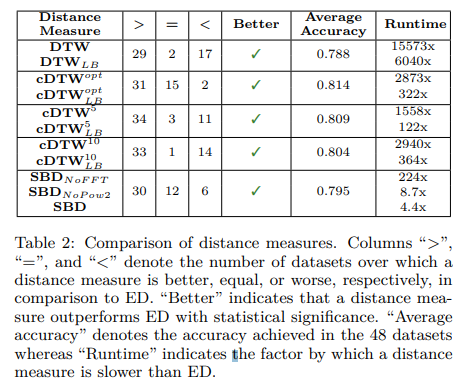
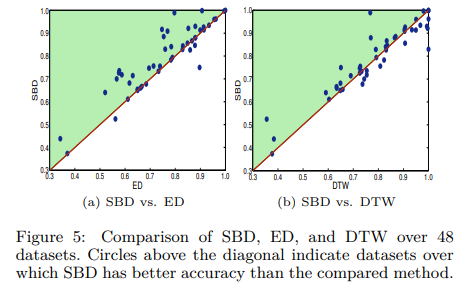
初步结论：

  • cDTW比DTW更快，精度更高
  • SBD比DTW更快，略低于ED
  • SBD fft+复杂度 权衡准确性和效率来说结果最好

不同聚类方法对比：

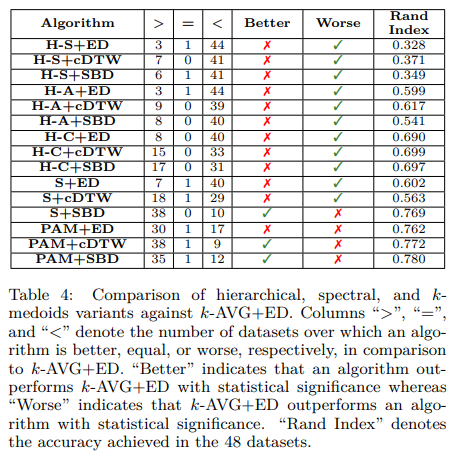
其中H表示层次聚类（H-S、H-A、H-C分别表示层次聚类的三种簇间距计算方式，Single Linkage 最近值，Complete Linkage最远值，Average Linkage平均值），S表示谱聚类，PAM表示Partitioning Around Medoi

相关资源

往年同期文章