1 常见距离测度
欧氏距离：对应元素求差后计算平方和（要求两个时序长度一致） $$ D(x,y) = \sqrt{(x_1-y_1)^2 + (x_2-y_2)^2 + ... + (x_n-y_n)^2} = \sqrt{\sum\limits_{i=1}^{n}(x_i-y_i)^2} $$ 曼哈顿距离：基于网格地图的路程（比如出租车的行驶路线长度） $$ D(x,y) =|x_1-y_1| + |x_2-y_2| + ... + |x_n-y_n| =\sum\limits_{i=1}^{n}|x_i-y_i| $$ 闵可夫斯基距离 (Minkowski Distance)： $$ D(x,y) =\sqrt[p]{(|x_1-y_1|)^p + (|x_2-y_2|)^p + ... + (|x_n-y_n|)^p} =\sqrt[p]{\sum\limits_{i=1}^{n}(|x_i-y_i|)^p} $$
欧式距离是闵可夫斯基距离距离在p=2时的特例，而曼哈顿距离是p=1时的特例
切比雪夫距离：两个向量在任意坐标维度上的最大差值 $$ D(x,y)=max(|x_1-y_1|,|x_2-y_2|,...,|x_n-y_n|) $$
2 动态时间规整
动态时间规整，Dynamic Time Warping（DTW）是一种衡量两个时间序列之间的相似度的方法
假定有两个时序$Q={q_1,q_2,...,q_n}$和$C={c_1,c_2,...,c_m}$，计算$DTW(Q,C)$过程如下：
- 构建大小为$n\times m$的矩阵$D$，矩阵元素$d_{ij}=dist(q_i,c_j)$，其中距离计算常用欧氏距离
- 在矩阵$D$中使用动态规划类算法搜索从$d_{11}$到$d_{nm}$的最短距离
- 将计算所得的最短距离作为时间序列$Q$和$C$的相似度
最终动态时间规整算法的时间复杂度为$O(mn)$，而通过约束方法，可以加快最短路径的计算过程
带约束的DTW，也就是constrained Dynamic Time Warping，简称cDTW
常见的两种全局约束方法（Sakoe-Chiba约束 和 Itakura-Parallelogram 约束）如下所示：
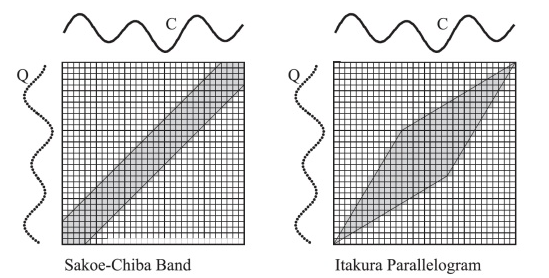
#DTW #cDTW #Sakoe-Chiba #Itakura-Parallelogram
3 互相关
互相关（Cross-correlation），有时也被称为互协方差或”滑动点积“
互相关的计算和卷积非常相似，所以很多人会混淆两种概念。但其实卷积计算会存在核翻转180°的操作，这样能保证卷积运算的可交换性，具体示例如下：
（参考自3.4.2-Spatial Correlation and Convonlution-Digital Image Processing 3ed Gonzalez）
编程计算时，对于边缘缺失的情况可以直接采用补零的操作
自相关是互相关的一种特殊情况，即两个时序相同。卷积、互相关、自相关对比如下：
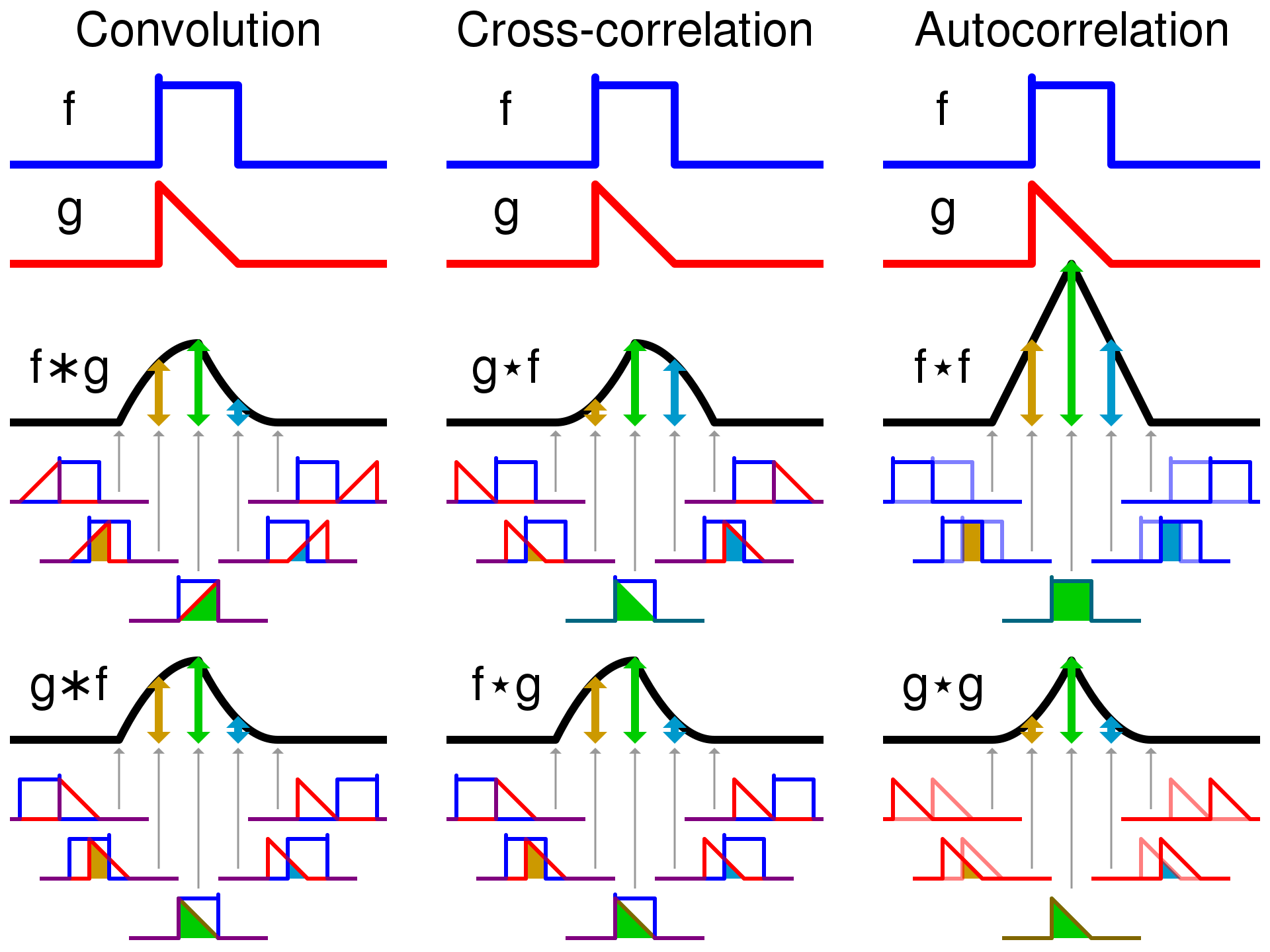（图源：https://en.wikipedia.org/wiki/Convolution）