分类目录归档：MIT18.01单变量微积分
Unit 1 知识点简单概
（最后一节课换了个导师，所以教学进度衔接似乎不太好 = =）
幂级数的性质1：存在收敛半径$R$ 幂级数的性质2：当$|x|<R$时，$f(x)$可无限求导（比如说多项式级数）
泰勒展开式：
$$f(x)=\Sigma_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n$$
示例1：几何级数 geometric series $\frac{1}{1+x}=1-x+x^2-x^3...(R=1)$
示例2：$ln(1+x)=\int_0^x\fr
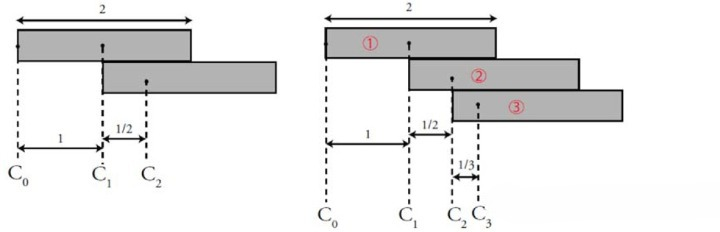
将1号木板放置在桌面边缘，在木板不掉落的情况下不断探出；然后再叠加2号木板，追求总探出长度最大的情况，以此类推，判断最终总长度是否是有限的
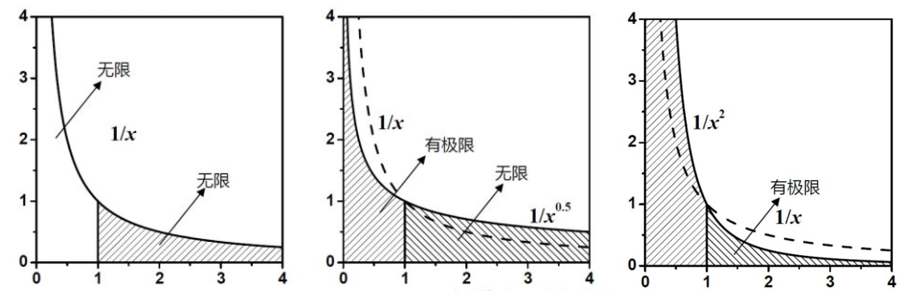
反常积分的第二种情况就是积分区域内有奇点的情况
示例：讨论$\int_0^1\frac{dx}{x^p}$的收敛性
总结3 反常积分示例中示例3的结果可得到以下结果：
芝诺悖论：$1+\frac{1}{2}+\frac
$$\begin{equation}
IF = \left\{
\begin{array}{rl}
f(x)\to \infty \\ \\
g(x)\to \infty \\ \\
\frac{f'(x)}{g'(x)}\to L
\end{array} \right.
\end{equation}
\ \ \ AS \ \ x\to a \ \ THEN \ \frac{f(x)}{g(x)}\
洛必达法则（L'Hopital's Rules）：当$f(a)=g(a)=0$
$$lim_{x\to a}\frac{f(x)}{g(x)}=lim_{x\to a}\frac{f(x)/(x-a)}{g(x)/(x-a)}=\frac{f'(x)}{g'(x)}(g'(x)\neq0)$$
$$lim_{x\to 0}\frac{sin5x}{sin2x}=lim_{x\to 0}\frac{5cos5x}{2cos2x}=\frac{5}{2}$$
$$lim_{x\to 0}\frac{cosx-
半径为$a$的圆的面积为$A=\pi a^2$
其中角度为$\Delta \theta$的扇形面积为$\Delta A$，则$\Delta A=\frac{\Delta \theta}{2\pi}\pi a^2=\frac{1}{2}a^2\Delta \theta$
无限细分角度，可得$dA=\frac{1}{2}a^2d\theta$，则$A=\int_{\theta_1}^{\theta_2}\frac{1}{2}a^2d\theta$
对于一些不规则的类圆图形，可引入参数方程，
$$x=acost,y=asint$$
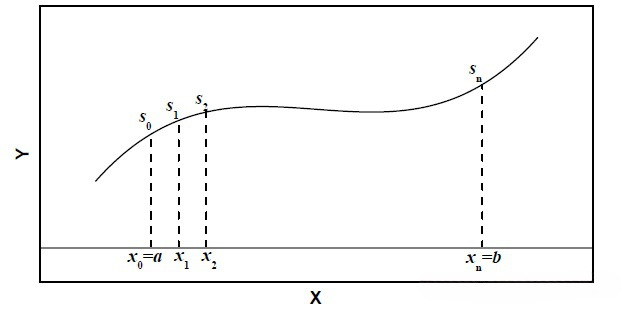
如上图所示，设$\Delta S=S_i-S_{i-1}$
部分分式：对满足比例函数$\frac{P(x)}{Q(x)}$形式的被积函数，通过代数的方式将其分解为容易进行积分的分式形式
分部积分法（integration by parts）是微