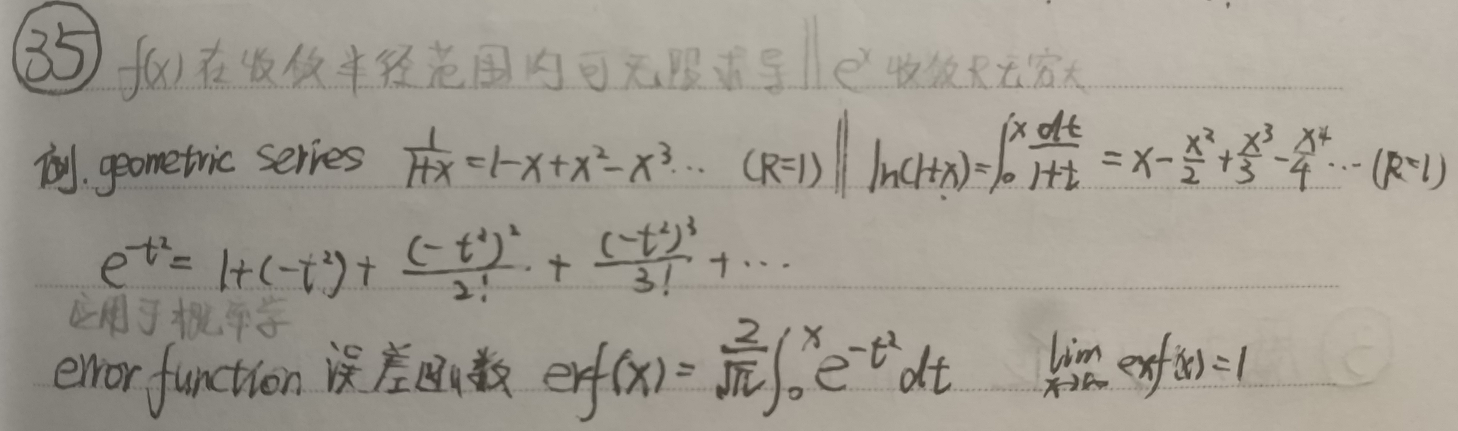1 泰勒级数补充
(最后一节课换了个导师,所以教学进度衔接似乎不太好 = =)
幂级数的性质1:存在收敛半径$R$ 幂级数的性质2:当$|x|<R$时,$f(x)$可无限求导(比如说多项式级数)
泰勒展开式:
$$f(x)=\Sigma_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n$$
2 示例与应用
示例1:几何级数 geometric series $\frac{1}{1+x}=1-x+x^2-x^3...(R=1)$
示例2:$ln(1+x)=\int_0^x\frac{dt}{1+t}=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}...(R=1)$
示例3:$e^{-t^2}=1+(-t^2)+\frac{(-t^2)^2}{2!}+\frac{(-t^2)^3}{3!}+...$
- 函数$e^{-t^2}$常用于概率学
- 比如作为误差函数(error function) $erf(x)=\frac{2}{\sqrt(\pi)}\int_0^xe^{-t^2}dt$
- $lim_{x\to \infty}exf(x)=1$
3 Unit 5 知识点简单概括
截止到第三十五节课,本课程的第五单元内容已完成,内容脉络简单梳理如下:
- 应用洛必达法则处理$\frac{0}{0}$和$\frac{\infty}{\infty}$的情况
- 推广普通积分,进行反常积分的探讨
- 探究几何级数、幂级数等常见无穷级数
- 研究级数的收敛性与收敛半径
- 借助泰勒展开用幂级数形式进行函数的表示
完结撒花
敬请期待 后续课程 MIT18.02多变量微积分
4 参考