LaTeX 是一种基于 ΤΕΧ 的排版系统,其中非常突出的是方便而强大的数学公式排版能力。
一、常用的数学符号
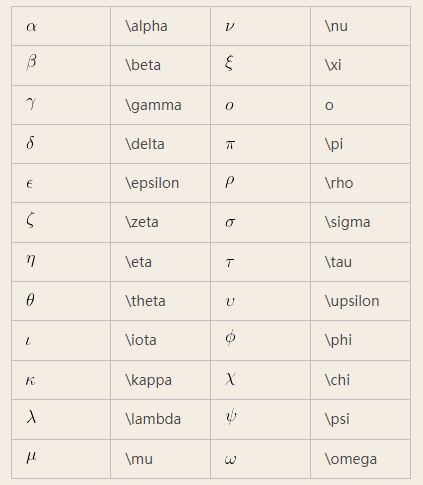
1 小写希腊字母
下面的都要上面这个案例一样才有用。两边只写了一个$的可以插在文本中,而两边写$$则会单独占一行,并且会居中而且还要大一些。
\varepsilon : $\varepsilon$
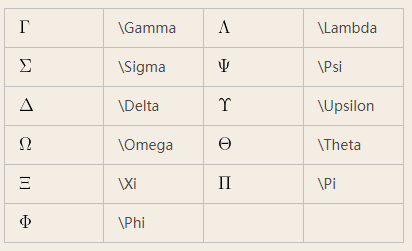
2 大写希腊字母
大写希腊字母只需要将小写希腊字母的第一个英文字母大写即可。但是需要注意的是,有些小写希腊字母的大写可以直接通过键盘输入,也就是说和英文大写是相同的。
其他常用特殊字母格式:
\mathcal{F}$\mathcal{F}$\textit{f}$\textit{f}$\text{f}$\text{f}$
3 运算符
加:+$+$, 减:-$-$,叉乘:\times $\times$ , 点乘:\cdot $\cdot$ ,点除:\div $\div$
普通字符 $ % & { }数学环境中表示时需要在字符前加上转义符号\ :$$%&_{}$
正负号:$\pm$ \pm ,波浪号:sim $\sim$,正相关\propto $\propto$
圈圈中的运算符:\otimes $\otimes$ \odot $\odot$ \oplus $\oplus$
对号:\checkmark$\checkmark$,星号\ast $\ast$
$\lfloor\text{文本}\rceil$ :\lfloor\text{文本}\rceil
二、简单格式
1 上下标
f(x) = x^2
f(x) = {x}^{2}
上标:$f(x) = x^2$ 或者 $f(x) = {x}^ {2}$
f(x) = x_2
f(x) = {x}_{2}
下标:$f(x) = x_2$ 或者 $f(x) = {x}_{2}$
f(x) = x_1^2 + {x}_{2}^{2}
上下标可以级联:$f(x) = x_1^2 + {x}_{2}^{2}$
2 加粗和倾斜
f(x) = \textbf{x}^2
加粗:$f(x) = \textbf{x}^2$
f(x) = x^2 \mbox{abcd}
文本:$f(x) = x^2 \mbox{abcd}$
f(x) = x^2 \mbox{\emph{abcd} defg}
倾斜:$f(x) = x^2 \mbox{\emph{abcd} defg}$ (注:网页暂不支持)
3 分数
f(x,y) = \frac{x^2}{y^3}
$$f(x,y) = \frac{x^2}{y^3}$$
4 开根号
f(x,y) = \sqrt[n]{{x^2}{y^3}}
$$f(x,y) = \sqrt[n]{{x^2}{y^3}}$$
5 省略号
f(x\_1, x\_2, \ldots, x\_n) = x\_1 + x\_2 + \cdots + x\_n
$$f(x_1, x_2, \ldots, x_n) = x_1 + x_2 + \cdots + x_n$$
6 字母上方加符号/下方加批注
加^号:$\hat{a}$ \hat{a}
加横线:$\overline{a}$ \overline{a}
加波浪线:$\widetilde{a}$ \widetilde{a}
加一个点:$\dot{a}$ \dot{a}
加两个点:$\ddot{a}$ \ddot{a}
加箭头:$\vec{a}$ \vec{a}
加大箭头:$\overrightarrow{a}$ \overrightarrow{a}
反向箭头:$\overleftarrow{a}$ \overleftarrow{a}
下标:$\mathop{max}\limits_{1<i<10}$ \mathop{max}\limits\_{1<i<10}
7 括号和分隔符
公式高度比较低的话直接从键盘输入括号即可,但是对于公式高度比较高的情形,需要特殊的运算。
{f}'(x) = (\frac{df}{dx})
$${f}'(x) = (\frac{df}{dx})$$
{f}'(x) = \left( \frac{df}{dx} \right)
$${f}'(x) = \left( \frac{df}{dx} \right)$$
可以看出,通过将 \left( 和 \right) 结合使用,可以将括号大小随着其内容变化。[ ] 和 { } 同理。
{f}'(0) = \left. \frac{df}{dx} \right|\_{x=0}
$${f}'(0) = \left. \frac{df}{dx} \right|_{x=0}$$
8 比较符号符
大于号:$\textgreater$ \textgreater (注:网页暂不支持)
小于号: $\textless$ \textless(注:网页暂不支持)
不等于:$\neq$ \neq
大于等于:$\geq$ \geq
小于等于:$\leq$ \leq
与等于:$\approx$ \approx
等价:$\sim$ \sim
9 箭头
$\uparrow$ \uparrow
$\downarrow$ \downarrow
$\updownarrow$ \updownarrow
$\rightarrow$ \rightarrow
$\leftarrow$ \leftarrow
$\leftrightarrow$ \leftrightarrow
$\Uparrow$ \Uparrow
$\Downarrow$ \Downarrow
$\Updownarrow$ \Updownarrow
$\Rightarrow$ \Rightarrow
$\Leftarrow$ \Leftarrow
$\Leftrightarrow$ \Leftrightarrow
$\iff$ \iff 等价于
三、矩阵和行列式
A=\left[ \begin{matrix}
a & b \\\\
c & d \\\\
\end{matrix} \right]
$$A=\left[ \begin{matrix} a & b \\ c & d \\ \end{matrix} \right]$$
\chi (\lambda)=\left| \begin{matrix}
\lambda - a & -b \\\\
-c & \lambda - d \\\\
\end{matrix} \right|
$$\chi (\lambda)=\left| \begin{matrix} \lambda - a & -b \\ -c & \lambda - d \\ \end{matrix} \right|$$
S=
\begin{bmatrix}
x\_{11} & x\_{12} & \cdots & x\_{1m} \\\\
x\_{21} & x\_{22} & \cdots & x\_{2m} \\\\
\vdots & \vdots & \ddots & \vdots \\\\
x\_{n1} & x\_{n2} & \cdots\ & x\_{nm} \\\\
\end{bmatrix}
$$S= \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots\ & x_{nm} \\ \end{bmatrix}$$
四、求和与连乘
\sum\_{k=1}^n k^2 = \frac{1}{2} n (n+1)
$$\sum_{k=1}^n k^2 = \frac{1}{2} n (n+1)$$
\prod\_{k=1}^n k = n!
$$\prod_{k=1}^n k = n!$$
五、导数、极限、积分
1 导数
导数的表示用一对花括号将被导函数括起来,然后加上一个英文的引号即可。
{f}'(x) = x^2 + x
$${f}'(x) = x^2 + x$$
2 偏导
\partial: 偏导符号
\mathrm{d}t:正规的导数d(正体)
$$\frac{\partial{y}}{\partial{x_1}}+\frac{\partial{y}}{\partial{x_2}}$$
$$\frac{\mathrm{d}y}{\mathrm{d}x}+\frac{\mathrm{d}z}{\mathrm{d}x}$$
梯度:\nabla $\nabla$
3 极限
\lim\_{x \to 0} \frac{3x^2 +7x^3}{x^2 +5x^4} = 3
$$\lim_{x \to 0} \frac{3x^2 +7x^3}{x^2 +5x^4} = 3$$
4 积分
积分中,需要注意的是,在多重积分内 dx 和 dy 之间 使用一个斜杠加一个逗号 , 来增大稍许间距。同样,在两个积分号之间使用一个斜杠加一个感叹号 ! 来减小稍许间距。使之更美观。
\int\_a^b f(x)\,dx
$$\int_a^b f(x),dx$$
\int\_0^{+\infty} x^n e^{-x} \,dx = n!
$$\int_0^{+\infty} x^n e^{-x} ,dx = n!$$
\int\_{x^2 + y^2 \leq R^2} f(x,y)\,dx\,dy =
\int\_{\theta=0}^{2\pi} \int\_{r=0}^R
f(r\cos\theta,r\sin\theta) r\,dr\,d\theta
$$\int_{x^2 + y^2 \leq R^2} f(x,y),dx,dy = \int_{\theta=0}^{2\pi} \int_{r=0}^R f(r\cos\theta,r\sin\theta) r,dr,d\theta$$
\int \\! \\! \\! \int\_D f(x,y)\,dx\,dy
\int \int\_D f(x,y)\,dx\,dy
$$\int \! \! \! \int_D f(x,y),dx,dy \int \int_D f(x,y),dx,dy$$
在加入了 ! 之后,距离的改变还是很明显的。(注:web暂不支持!)
i\hbar\frac{\partial \psi}{\partial {t}} = \frac{-\hbar^2}{2m}
\left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} +
\frac{\partial^2}{\partial z^2} \right) \psi + V \psi
$$i\hbar\frac{\partial \psi}{\partial {t}} = \frac{-\hbar^2}{2m} \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right) \psi + V \psi$$
\frac{d}{dt} \int \\! \\! \\! \int \\! \\! \\! \int\_{\textbf{R}^3} \left
| \psi(\mathbf{r},t) \right|^2\,dx\,dy\,dz = 0
$$\frac{d}{dt} \int \! \! \! \int \! \! \! \int_{\textbf{R}^3} \left | \psi(\mathbf{r},t) \right|^2,dx,dy,dz = 0$$
注意:Obsidian暂不支持闭合积分,暂时可使用unicode符号∮ ∯∰表示
六、公式并排和方程组
1 长公式「被迫」折行
使用multline 环境,实现首行局左,中间居中,末行局右
\begin{multline}
p = 3x^6 + 14x^5y + 590x^4y^2 + 19x^3y^3 \\\\
+ \sin{x} + \cos{y} + \tan{a} + e^{x+y} \\\\
- 12x^2y^4 - 12xy^5 + 2y^6 - a^3b^3
\end{multline}
$$\begin{multline} p = 3x^6 + 14x^5y + 590x^4y^2 + 19x^3y^3 \\ + \sin{x} + \cos{y} + \tan{a} + e^{x+y} \\ - 12x^2y^4 - 12xy^5 + 2y^6 - a^3b^3 \end{multline}$$
2 多行公式带编号
\begin{align}
a & = b + c \tag{1}
\\[3pt]
& = d + e \tag{2}
\end{align}
$$\begin{align} a & = b + c \tag{1} \ \\ & = d + e \tag{2} \end{align} $$
3 多行多列公式
\begin{align}
a &=1 & b &=2 & c &=3 \\
d &=-1 & e &=-2 & f &=-5
\end{align}
$$\begin{align} a &=1 & b &=2 & c &=3 \\ d &=-1 & e &=-2 & f &=-5 \end{align} $$
4 方程组
\begin{equation}
\left\\{
\begin{gathered}
a\_{11} x\_{1} + a\_{12} x\_{2} + a\_{13} x\_{2} = b\_{1}
\ \\\\
a\_{21} x\_{1} + a\_{22} x\_{3} + a\_{23} x\_{3} = b\_{2}
\end{gathered}
\right.
\end{equation}
$$\begin{equation} \left\{ \begin{gathered} a_{11} x_{1} + a_{12} x_{2} + a_{13} x_{2} = b_{1} \ \\ a_{21} x_{1} + a_{22} x_{3} + a_{23} x_{3} = b_{2} \end{gathered} \right. \end{equation} $$
5 带条件方程组
\begin{equation}
|x| = \left\{
\begin{array}{rl}
-x & \mbox{if } x < 0,\\
0 & \mbox{if } x = 0,\\ \tag{1}
x & \mbox{if } x > 0.
\end{array} \right.
\end{equation}
$$\begin{equation} |x| = \left\{ \begin{array}{rl} -x & \mbox{if } x < 0, \\ 0 & \mbox{if } x = 0, \\ \tag{1} x & \mbox{if } x > 0. \end{array} \right. \end{equation} $$
七、向量与集合
常见向量关系:
perp 垂直 $\perp$
常见集合关系:
\mathbb{R} 特殊集合符号:$\mathbb{R}$ $\mathbb{Z}$ $\mathbb{X}$ $\mathbb{N}$
\in 表示属于 $\in$
\notin 表示不属于 $\notin$
\subset 包含于 $\subset$
\subseteq 包含于 $\subseteq$
\supset 包含 $\supset$
\cup \cap \complement_SA 交并补 $\cup \cap \complement_SA$
任意 \forall $\forall$
存在 \exists $\exists$
八、统计概率
{n \choose 2}抽样组合${n \choose 2}$