1 回顾-部分分式通用过程
部分分式:对满足比例函数$\frac{P(x)}{Q(x)}$形式的被积函数,通过代数的方式将其分解为容易进行积分的分式形式
- 长除法,确保余式分子最高项小于分母
- 分母因式分解,将高次复杂的分母转为低次简单连乘的形式
- 对分母建立等式,拆分复杂的分数为多简单分数相加的形式,并在分子中设未知数
- 掩盖法求解,个别项通过对比等式两侧系数,建立线性方程组求解
- 对各个部分进行积分,并得到被积函数的积分结果,注意小尾巴(常数C)
2 分部积分
分部积分法(integration by parts)是微积分基本定理和乘法求导法则的结合。 $$\int_a^buv'dx=uv|_a^b-\int_a^bu'vdx$$
分部积分中$u$的一般选择顺序:反对幂指三
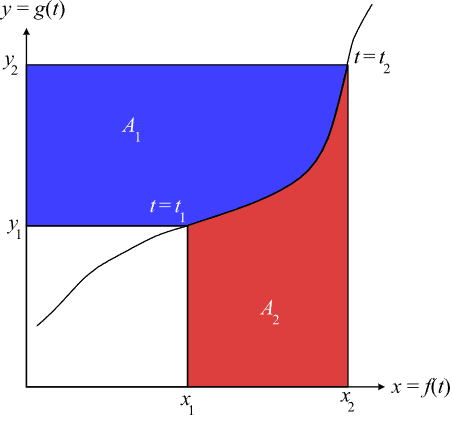
几何解释(来自维基百科):
$$\int_{x_1}^{x_2}ydx+\int_{y_1}^{y_2}xdy=xy(x)|_{x_1}^{x_2}$$
3 分部积分示例
$$\int{(lnx)^n}dx=(lnx)^nx-\int{xd(lnx)^n}=(lnx)^nx-n\int{(lnx)^{n-1}}dx$$
$$\int{x^ne^x}dx=x^ne^x-\int{e^xdx^n}=x^ne^x-n\int{x^{n-1}e^x}dx$$
4 参考
