1 弧长 arc length
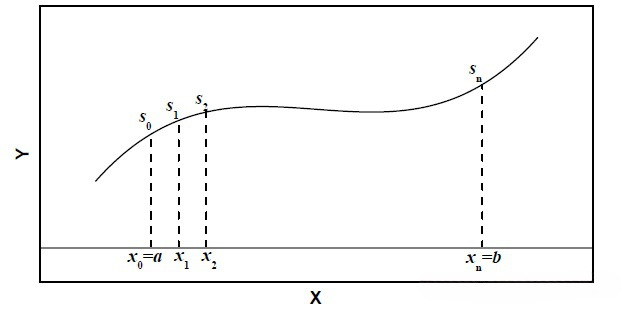
如上图所示,设$\Delta S=S_i-S_{i-1}$
- 将弧长近似为线段,由此可得$(\Delta S)^2 \approx(\Delta x)^2+(\Delta y)^2$
- 无限细化$S_i$与$S_{i-1}$之间的距离,可得$(ds)^2 =(dx)^2+(dy)^2$
- 化简得$ds=\sqrt{1-(\frac{dy}{dx})^2}dx$
- 从$S_0$到$S_n$的总弧长$=\int_a^bds=\int_a^b\sqrt{1-(\frac{dy}{dx})^2}dx=\int_a^b\sqrt{1-f'(x)^2}dx$
2 弧长计算示例
题目:计算以下函数图像($y=\sqrt{1-x^2}$)中的弧长$\alpha$
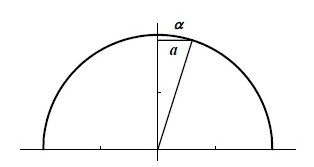
- 由上一节可知,$\alpha=\int_0^a\sqrt{1-y'^2}dx$
- 化简可得,$\int_0^a\sqrt{1-y'^2}dx=\int_0^a\frac{dx}{\sqrt{1-x^2}}=arcsina$
- 通过对弧长的计算,诞生了$\alpha =arcsina$,进而产生了$sin\alpha=a$
- 这是一次严密的导出过程,也是三角函数的一种推演与诞生
3 曲面面积 surface area
弧长的计算理论也适用于求曲面面积
题目:求解函数$y=x^2$绕$x$轴旋转后的旋转体面积(the surface of ratation)A
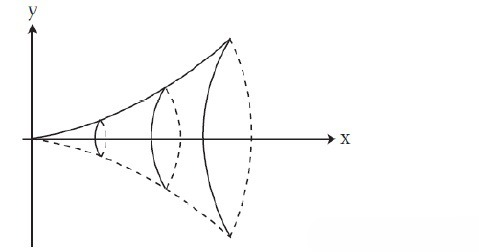
- 按照极限近似的思想可得$dA=(2\pi y)(ds)$
- 由此可得,$A=\int_0^a2\pi x^2\sqrt{1+4x^2}dx$
- 下一步使用换元法,带入$x=\frac{1}{2}tan\mu$,后续计算略
4 参数方程 parametric curves
使用参数(parametric)$t$ 表示整个方程,即$x=x(t), y=y(t)$
具体的应用示例将放在下一节
5 参考
