1 极坐标与面积
半径为$a$的圆的面积为$A=\pi a^2$
其中角度为$\Delta \theta$的扇形面积为$\Delta A$,则$\Delta A=\frac{\Delta \theta}{2\pi}\pi a^2=\frac{1}{2}a^2\Delta \theta$
无限细分角度,可得$dA=\frac{1}{2}a^2d\theta$,则$A=\int_{\theta_1}^{\theta_2}\frac{1}{2}a^2d\theta$
对于一些不规则的类圆图形,可引入参数方程,令$r=r(\theta)$
2 极坐标与面积示例
题目1:计算$r=2acos\theta(-\frac{\pi}{2}\geq \theta\geq \frac{\pi}{2})$时,所构图像面积$A$
$A=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{2}(2acos\theta)^2d\theta =\pi a^2$
- $r=2acos\theta$构建的图像就是圆心在$(a,0)$,半径为$a$的圆
- 此题目也是从定积分的角度得出了圆的面积公式
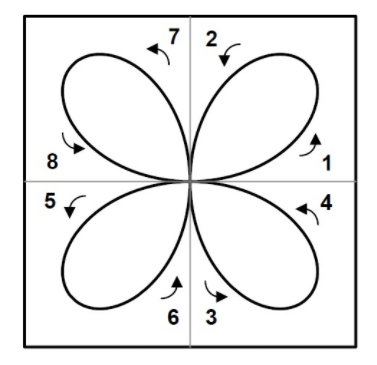
题目2:绘制$r=sin2\theta$的函数图像
| $r$ | $0$ | $1$ | $0$ | .... |
|---|---|---|---|---|
| $\theta$ | $0$ | $\frac{\pi}{4}$ | $\frac{\pi}{2}$ | .... |
- 选择不同的$r$与$\theta$的特殊点,构建表格并用于绘图
- 最终的函数图像被称之为四叶玫瑰(four-leaf rose)
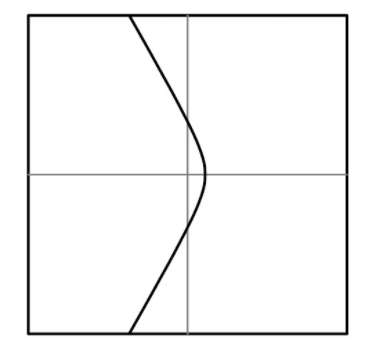
题目3:绘制$r=\frac{1}{1+2cos\theta}$的函数图像
| $r$ | $\frac{1}{3}$ | $1$ | $1$ | .... |
|---|---|---|---|---|
| $\theta$ | $0$ | $\frac{\pi}{2}$ | $-\frac{\pi}{2}$ | .... |
- 选择不同的$r$与$\theta$的特殊点,构建表格并用于绘图
- 当$2cos\theta =1$,即$\theta= \pm\frac{2}{3}\pi$时,$r$趋近于无穷
- 将参数方程转为指标坐标系方程:$r=1-2rcos\theta=1-2x$
- 由$r^2=(1-2x)^2=x^2+y^2$可得,$-3x^2+y^2+4x-1=0$
- 上式为双曲线(hyperbola)函数
- 当$\theta \in [-\frac{2}{3\pi},\frac{2}{3\pi}]$时,对应双曲线的另一条
补充:双曲线、开普勒定律与角动量守恒
- 双曲线是彗星的轨道,椭圆则是行星或小行星的轨道
- $r=0$时对应的是双曲线的焦点,即太阳所在,这也是物理绘图时把重心作为坐标原点的依据
- $dA=\frac{1}{2}r^2d\theta$是天文学的核心公式,以开普勒定律(行星和太阳的连线在相等的时间间隔内扫过的面积相等)为例
- $\frac{dA}{dt}=\frac{1}{2}r^2\frac{d\theta}{dt}=C$,这说明在无摩擦的情况下,物体旋转后会以大致相同的比率继续旋转(也就是角动量守恒 conservation of angular momentum)
- 由于$C$是不变的(只取决于中心质量,如太阳),所以当减小$r$时,$\frac{d\theta}{dt}$会变大,这也是滑冰运动员让自己蜷缩时会增大转速的原因
3 Unit 4 知识点简单概括
截止到第三十节课,本课程的第四单元部分内容已完成,内容脉络简单梳理如下:
- 特定三角函数的积分通解(三角替换)
- 借助换元法和配方法研究带三角函数的积分求解
- 借助“掩盖”法对积分公式中的线性因子进行拆分,以简化计算
- 借助分部积分法对部分特殊的积分进行简化
- 研究参数方程,并结合积分进行弧长、面积的求解
4 参考
