时序差分算法 TD
发表评论
3 views

前置知识：1_study/MachineLearning/强化学习/强化学习入门、蒙特卡洛法、马尔可夫决策过程 MDP

时序差分算法

时序差分（temporal difference，TD）

  • 一种用来估计一个策略的价值函数的方法，结合了蒙特卡洛和动态规划算法的思想
  • 时序差分 vs 蒙特卡洛：都可以从样本数据中学习，不需要事先知道环境；但蒙特卡洛法需要完成整个序列后才能计算得到回报 $G_{t}$，而时序差分法只需要当前步结束即可进行计算
  • 时序差分 vs 动态规划：都可以根据贝尔曼方程来更新当前状态的价值估计

回顾 MDP 中状态价值函数的贝尔曼方程： $$ v_{\pi}(s) =  \mathbb{E}_{\pi}(R_{t+1} + \gamma v_{\pi}(S_{t+1}) | S_t=s) $$

  • 其中 $R_{t+1} + \gamma v_{\pi}(S_{t+1})$ 被称为 TD 目标值，可近似替代时刻 $t$ 的回报 $G_{t}$；即回报 $G_{t}$ 近似等于当前获得奖励的折现 $\gamma v_{\pi}(S_{t+1})$ 加上下一个状态的价值估计 $R_{t+1}$
  • $R_{t+1} + \gamma v_{\pi}(S_{t+1})-v_{\pi}(S_{t})$ 被称为 TD 误差 $\delta_{t}$，表示状态价值单次迭代时的更新量
  • 引入范围在 $[0,1]$ 的参数 $\alpha$ 来定义每次状态价值更新的步长；最终状态价值函数 $v_{\pi}(S_{t})$ 和动作价值函数 $q_{\pi}(S_{t},A_{t})$ 的函数迭代公式如下：

$$ \begin{equation} \left\{ \begin{gathered} v_{\pi}(S_{t})=v_{\pi}(S_{t})+\alpha(G_{t}-v_{\pi}(S_{t}))=v_{\pi}(S_{t})+\alpha \ \delta_{t} \ \\ q_{\pi}(S_{t},A_{t})=q_{\pi}(S_{t},A_{t})+\alpha(G_{t}-q_{\pi}(S_{t},A_{t}))=q_{\pi}(S_{t},A_{t})+\alpha \ \delta_{t} \end{gathered} \right. \end{equation} $$

时序差分总结与分析：

  • 时序差分可以在与环境的交互中持续学习，快速更新状态价值的估计
  • TD 目标值是对当前状态价值（回报）的有偏估计，而蒙特卡洛法是无偏估计
  • 相比于蒙特卡洛法，TD 算法得到的结果方差更低，对初始值敏感，效率更高

时序差分的常见在线策略（on-policy）算法是 SARSA；时序差分的常见离线策略（off-policy）算法是 Q-Learning；这两种算法都将在下文中进行具体说明

N 步时序差分

N 步时序差分：用当前奖励和未来 N 步内状态的预估价值来近似替代回报 $G_{t}$

引入范围在 $[0,1]$ 的参数 $\lambda$ 来定义第 $n$ 步回报权重为 $(1-\lambda)\lambda^{n-1}$ ，则回报 $G_{t}$ 可表示为 $$ G_t^{(n)} = R_{t+1} + \gamma  R_{t+2} + ... + \gamma^{n-1} R_{t+n}  + \gamma^nv_{\pi}(S_{t+n}) $$

  • 由上式可知，随着步数 $n$ 的增加，第 $n$ 步回报的权重呈几何级数的衰减，终止状态保留未分配的权重，确保完整序列的回报的权重之和为 1

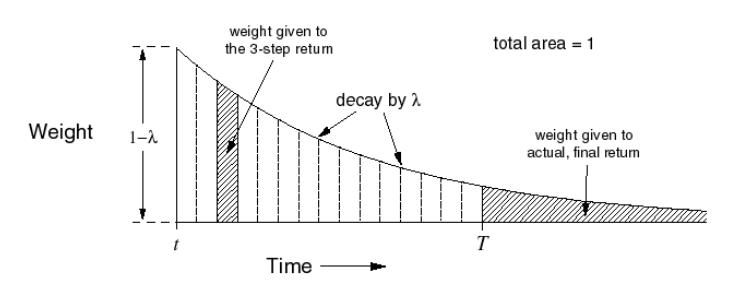
当 $\lambda=0$ 时，N 步时序方差退化为普通时序差分，当 $\lambda=1$ 时，N 步时序方差就是蒙特卡洛法

为状态 $s$ 引入效用 (eligibility, E) 来表示该状态对后续状态的影响，即 $E(s)$；所有状态的效用值总称为效用迹(eligibility traces, ES)。假设每个状态的初始效用 $E_{0}(s)=0$ ，可得状态 $s$ 在时刻 $k$ 的效用为： $$ E_t(s) = \gamma\lambda E_{t-1}(s) +1(S_t=s) = \begin{cases} 0& {t<k} \\ (\gamma\lambda)^{t-k}& {t\geq k} \end{cases}, ;;s.t.; \lambda,\gamma \in [0,1], s; is; visited ;once;at; time; k $$

  • 效用综合考虑价值衰减因子 $\gamma$ 和回报衰减因子 $\lambda$，来描述状态对后续状态的影响

最终 N 步时序差分的状态价值函数 $v_{\pi}(S_{t})$ 和动作价值函数 $q_{\pi}(S_{t},A_{t})$ 的函数迭代公式如下： $$ \begin{equation} \left\{ \begin{gathered} v_{\pi}(S_{t})=v_{\pi}(S_{t})+\alpha E_t(s)\ \delta_{t} \ \\ q_{\pi}(S_{t},A_{t})=q_{\pi}(S_{t},A_{t})+\alpha E_t(s)\ \delta_{t} \end{gathered} \right. \end{equation} $$

SARSA 算法

SARSA 是一种基于时序差分的在线策略强化学习算法

  • 作为一种在线策略，SARSA 不区分行为策略和目标策略
  • SARSA 依赖时序差分来进行策略的状态价值函数估计
  • SARSA 用 $\epsilon$-贪婪算法来进行策略的质量提升

$\epsilon$ -贪婪算法：有 $1-\epsilon$ 概率根据价值最大来选择动作，有 $\epsilon$ 概率随机选择动作；

SARSA 算法步骤

  1. 随机初始化所有状态 $S_{0}$ 和动作价值 $q_{\pi}(S_{0},A_{0})$，终止状态价值为 0
  2. 假设时刻 $t$ 的状态为 $S_{t}$，此时根据 $\epsilon$ -贪婪算法选择动作 $A_{t}$
  3. 执行动作 $A_{t}$，得到下一刻的状态 $S_{t+1}$ 和奖励 $R_{t+1}$
  4. 根据 $\epsilon$ -贪婪算法在状态 $S_{t+1}$ 下选择动作 $A_{t+1}$
  5. 根据价值函数计算 TD 误差 $\delta_{t} = R_{t+1} + \gamma q_{\pi}(S_{t+1},A_{t+1})-q_{\pi}(S_{t},A_{t})$
  6. 以 $\alpha$ 作为步长，更新价值函数 $q_{\pi}(S_{t},A_{t})=q_{\pi}(S_{t},A_{t})+\alpha \delta_{t}$
  7. 重复步骤 2~6，直到状态 $S_{t+1}$ 为终止状态

注意步长 $\alpha$ 需要随着迭代的进行逐渐减少，确保动作价值 $q_{\pi}$ 是可收敛的

多步 SARSA 算法

  • 基于 N 步时序差分版本的 SARSA 算法
  • 主要改动在于，引入效用迹函数 $E_{t}$ 来修正 TD 误差

$$ \delta_{t}^{new} = R_{t+1} + \gamma q_{\pi}(S_{t+1},A_{t+1})+\dots+\gamma^n q_{\pi}(S_{t+n},A_{t+n})-q_{\pi}(S_{t},A_{t})=E_{t}\delta_{t} $$

  • 在迭代过程中，注意同步更新效用迹函数 $E_t(s) = \gamma\lambda E_{t-1}(s) +1$

SARSA 算法总结与分析：

  • 使用灵活，不依赖环境的状态转移模型，价值估计也不需要完整序列
  • 不是用于较为复杂的问题，尤其是状态空间或动作空间维度较大的情况

Q-Learning

Q-learning 是一种基于时序差分的离线策略强化学习算法

  • 作为一种离线策略，Q-learning 的时序差分计算不依赖于当前策略
  • 对于行为策略，Q-learning 和 SARSA 一样采用 $\epsilon$ -贪婪算法
  • 对于价值函数更新，Q-learning 则采用贪婪法直接优化价值函数

Q-learning 算法步骤

  1. 随机初始化所有状态 $S_{0}$ 和动作价值 $q_{\pi}(S_{0},A_{0})$，终止状态价值为 0
  2. 假设时刻 $t$ 的状态为 $S_{t}$，此时根据 $\epsilon$ -贪婪算法选择动作 $A_{t}$
  3. 执行动作 $A_{t}$，得到下一刻的状态 $S_{t+1}$ 和奖励 $R_{t+1}$
  4. 根据贪婪算法找到在状态 $S_{t+1}$ 下的最优动作 $A^*$
  5. 根据价值函数计算 TD 误差 $\delta_{t} = R_{t+1} + \gamma q_{\pi}(S_{t+1},A^*)-q_{\pi}(S_{t},A_{t})$
  6. 以 $\alpha$ 作为步长，更新价值函数 $q_{\pi}(S_{t},A_{t})=q_{\pi}(S_{t},A_{t})+\alpha \delta_{t}$
  7. 重复步骤 2~6，直到状态 $S_{t+1}$ 为终止状态

Q-learning 算法总结与分析：

  • Q-learning 采用贪婪算法直接学习最优策略，而 SARSA 则在学习最优策略的同时还在做探索；因此SARSA 的学习过程会更平滑，而Q-learning 则更激进，可能存在不收敛的情况
  • SARSA 和 Q-learning 更适用于小规模数据下的强化学习问题，二者在面对复杂的状态空间和动作时，均需要维护庞大的 Q 表（内存占用高），此时可考虑使用基于深度学习的 RL 方法

在模拟环境中强化学习推荐使用Q-Learning，如果是在线生产环境中则推荐使用SARSA

参考

强化学习（五）用时序差分法（TD）求解
强化学习（六）时序差分在线控制算法 SARSA 强化学习（七）时序差分离线控制算法 Q-Learning
动手学强化学习 - 第 5 章 时序差分算法

往年同期文章