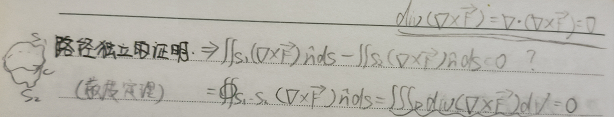1 单连通区域
定义单连通区域:区域内的任意一个闭合回路,在该区域内都有一个以它为界的曲面
举例理解:
- 三维空间去除一个原点后,此区域为单连通区域
- 三维空间去除$z$轴后,此区域为非连通区域
拓扑学拓展(通过”独立“环路数对曲面进行初步分类):
- “甜甜圈”形状(doughnut)曲面:横切得到的环路由于内部存在洞所以找不到曲面,竖切得到的环路无法是任何曲面的边界,这两种”独立“环路都不能用于界定曲面边界
- 莫比乌斯环和克莱因瓶:属于不可定向(no-orientable)曲面,比如莫比乌斯环是单侧曲面,所以无法定义正反面(右手定则失效),这种场景通量也就无法被定义

2 斯托克斯定理与曲面独立性
复习梯度场、保守场、路径独立的相关结论:
- 如果$\vec{F}=\nabla f$是梯度场,则旋度$curl\vec{F}=0$
- (逆命题)如果$\vec{F}$定义在单连通空间且$curl\vec{F}=0$,则$\vec{F}$是梯度场
- $\vec{F}$是梯度场、$\vec{F}$是保守场、$\vec{F}$的线积分结果与路径无关,这三个结论是等价的
简单证明$\vec{F}$线积分的路径独立:
- 已知$\vec{F}$定义在单连通空间且$curl\vec{F}=0$
- 在单连通区域$R$中,构建两个起止点相同的曲线$C_1$和$C_2$
- 由于起止点相同,所以曲线$C_1$和$C_2$可以构成闭合曲线$C=C_1-C_2$
- 所以$\int_{C_1}\vec{F}\cdot d\vec{r}-\int_{C_2}\vec{F}\cdot d\vec{r}=∮_C\vec{F}\cdot d\vec{r}=\int!!!\int_S(\nabla \times \vec{F})\cdot \hat{n}dS=0$
以闭合曲线$C$为边界,构建两个不太的曲面$S_1$和$S_2$,根据斯托克斯定理可知: $$∮_C\vec{F}\cdot d\vec{r}=\int \! \! \!\int_{S_1}(\nabla \times \vec{F})\cdot \hat{n}dS=\int \! \! \!\int_{S_1}(\nabla \times \vec{F})\cdot \hat{n}dS$$ 即斯托克斯定理认为,空间线积分的结果具备曲面独立性
曲面独立性的证明:
- 由于曲面$S_1$和$S_2$的边界一致,所以二者可以拼接为闭合曲面$S_1-S_2$
$$\int \! \! \!\int_{S_1}(\nabla \times \vec{F})\cdot \hat{n}dS-\int \! \! \!\int_{S_1}(\nabla \times \vec{F})\cdot \hat{n}dS = ∯_{S_1-S_2}(\nabla \times \vec{F})\cdot \hat{n}dS$$
- 假设闭合曲面$S_1-S_2$包围形成的空间为$D$,则根据散度定理,可得:
$$∯_{S_1-S_2}(\nabla \times \vec{F})\cdot \hat{n}dS=\int \! \! \!\int \! \! \!\int_Ddiv(\nabla \times \vec{F})\cdot \hat{n}dS=\int \! \! \!\int \! \! \!\int_D\nabla\cdot(\nabla \times \vec{F})\cdot dV $$
- 已知任意两个向量$u,v$的叉乘结果$u\times v$与两个向量组成平面垂直,所以任意叉乘结果与向量的点积$:u\cdot (u\times v)$恒等于0:
$$\int \! \! \!\int \! \! \!\int_Ddiv(\nabla \times \vec{F})\cdot dV=\int \! \! \!\int \! \! \!\int_D\nabla\cdot(\nabla \times \vec{F})\cdot dV=0$$
3 第四次复习
截止到第三十二节课,本课程的第四单元:三维空间中的三重积分和曲面积分(Unit 4 Triple integrals and surface integrals in 3-space)内容已完成,内容脉络简单梳理如下:
- 不同坐标系下的三重积分的计算(直角坐标系、柱坐标系、球坐标系)
- 不同坐标系下的三重积分的应用(体积、质量、质心、转动惯量)
- 三维向量场与面积分(通量、通量的计算、散度定理、扩散方程)
- 空间线积分与做功(线积分基本定理、保守场、势函数、旋度)
- 斯托克斯定理(右手定则、单连通区域、曲面分类、曲面独立性)
补充说明:
- 本单元内容的很多内容都是建立在上一单元的知识基础上,内容存在一定的重复
- 但伴随着维度的提高,很多理论也进行了进阶与拓展,十分值得进行深入的思考
- 原本二维空间中的格林公式(将线积分转为二重积分),在三维空间既可拓展为散度定理(将面积分转为三重积分),也可拓展为斯托克斯定理(将线积分转为面积分)
- 而在更高维度上,格林公式的变化与拓展或许会更加地丰富与有趣
4 参考