1 半角公式 half-angle formula
$$cos^2\theta = \frac{1+cos(2\theta)}{2}$$
$$sin^2\theta = \frac{1-cos(2\theta)}{2}$$
2 特定三角函数的积分通解
$$\int sin^mxcos^nxdx$$
以上形式的积分,对于任意的$m、n$存在通解
下面将分为两种情况讨论并证明
2.1 情况1:至少有一个指数是奇数
此时,从奇指数项中,提取最高次数的偶次数,例题如下:
$$\int sin^3xcos^2xdx=\int(1-cos^2x)sinxcos^2xdx=\int (cos^2x-cos^4x)sinxdx=\int(u^4-u^2)du$$
2.2 情况2:两个指数都为偶数
此时,直接带入半角公式,例题如下:
$$\int sin^2xcos^2xdx=\int(\frac{1+cos2x}{2}\frac{1-cos2x}{2})dx=\int \frac{1-cos^22x}{4}dx$$
3 三角替换的应用
题目:求下图中阴影的面积
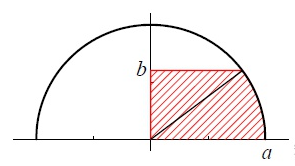
- 转换视角,考虑从另一个方向进行积分
- $Area=\int xdy=\int_0^b\sqrt{a^2-y^2}dy$
- 根据圆的几何关系可得:$x=acos\theta,y=asin\theta$
- 带入化简可得:$Area=acos\theta dasin\theta=a^2cos^2\theta d\theta=a^2(\frac{\theta}{2}+\frac{sin2\theta}{4})|_0^{arcsin\frac{b}{a}}$
4 参考
