个人笔记

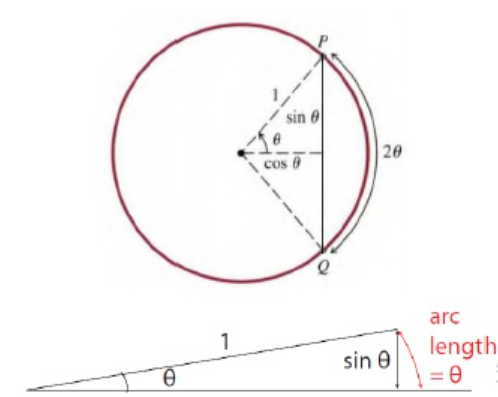
1 三角函数的微积分

三角函数恒等式：

$$secx=\frac{1}{cosx}$$ $$cscx=\frac{1}{sinx}$$ $$cotx=\frac{cosx}{sinx}$$ $$sec^2x=\frac{1}{cos^x}=1+tan^2x$$

三角函数的微积分：

$$tan'x=sec^2x$$ $$sec'x=secx\ tanx$$ $$\int tanx=-ln(cos)+C$$ $$\int secx=ln(secx+tanx)+C$$

证明：$\int secx=ln(secx+tanx)

Read more

1 半角公式 half-angle formula

$$cos^2\theta = \frac{1+cos(2\theta)}{2}$$

$$sin^2\theta = \frac{1-cos(2\theta)}{2}$$

2 特定三角函数的积分通解

$$\int sin^mxcos^nxdx$$

以上形式的积分，对于任意的$m、n$存在通解

下面将分为两种情况讨论并证明

2.1 情况1：至少有一个指

Read more

1 求导公式

1. 特定函数求导，如$x^n$的导数为$nx^{n-1}$
2. 通用公式，如${(u+v)}'={u}'+{v}'$
3. 以上两种的混合使用

2 三角函数的导数

• 在正式推导前，需要先推导出两个特殊情况下的极限变化率

第一种特殊情况： $$\lim_{x \to 0}\frac{sin(x)}{x}=1$$ 几何法证明：

（图片引用说明：知乎@三少爷的贱男春）

• 上图为一个标准单位圆，角度$\theta$对应弧长为$2\pi r=\theta$
• 随着$\theta$的减少，极短曲线可看作直线，即$\theta=sin(\theta

Read more