1 求导公式
- 特定函数求导,如$x^n$的导数为$nx^{n-1}$
- 通用公式,如${(u+v)}'={u}'+{v}'$
- 以上两种的混合使用
2 三角函数的导数
- 在正式推导前,需要先推导出两个特殊情况下的极限变化率
第一种特殊情况: $$\lim_{x \to 0}\frac{sin(x)}{x}=1$$ 几何法证明:
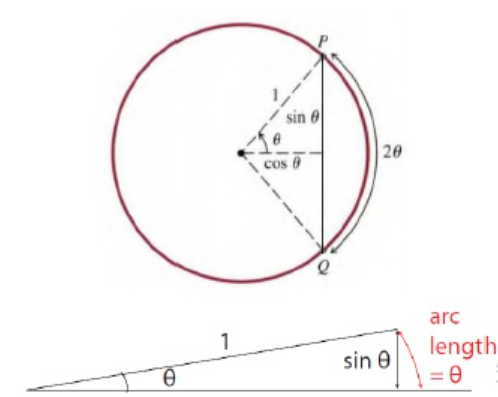
(图片引用说明:知乎@三少爷的贱男春)
- 上图为一个标准单位圆,角度$\theta$对应弧长为$2\pi r=\theta$
- 随着$\theta$的减少,极短曲线可看作直线,即$\theta=sin(\theta)$
第二种特殊情况: $$\lim_{x \to 0}\frac{coss(x)-1}{x}=0$$
- 可以考虑用类似于第一种特殊情况的几何法证明,不过
函数$sin(x)$求导推理 $$\begin{align} (sin(x))' & =\lim_{\Delta x \to 0}\frac{sin(x+\Delta x)-sin(x)}{\Delta x} \ \\ & = \lim_{\Delta x \to 0}\frac{sin(x)cos(\Delta x)+cos(x)sin(\Delta x)-sin(x)}{\Delta x} \ \\ & = \lim_{\Delta x \to 0}\frac{sin(x)(cos(\Delta x)-1)+cos(x)sin(\Delta x)}{\Delta x} \ \\ & = cos(x) \end{align}$$
函数$cos(x)$求导推理过程是类似的,略了 $$(cos(x))'=-sin(x)$$
参考