1 反常积分2
反常积分的第二种情况就是积分区域内有奇点的情况
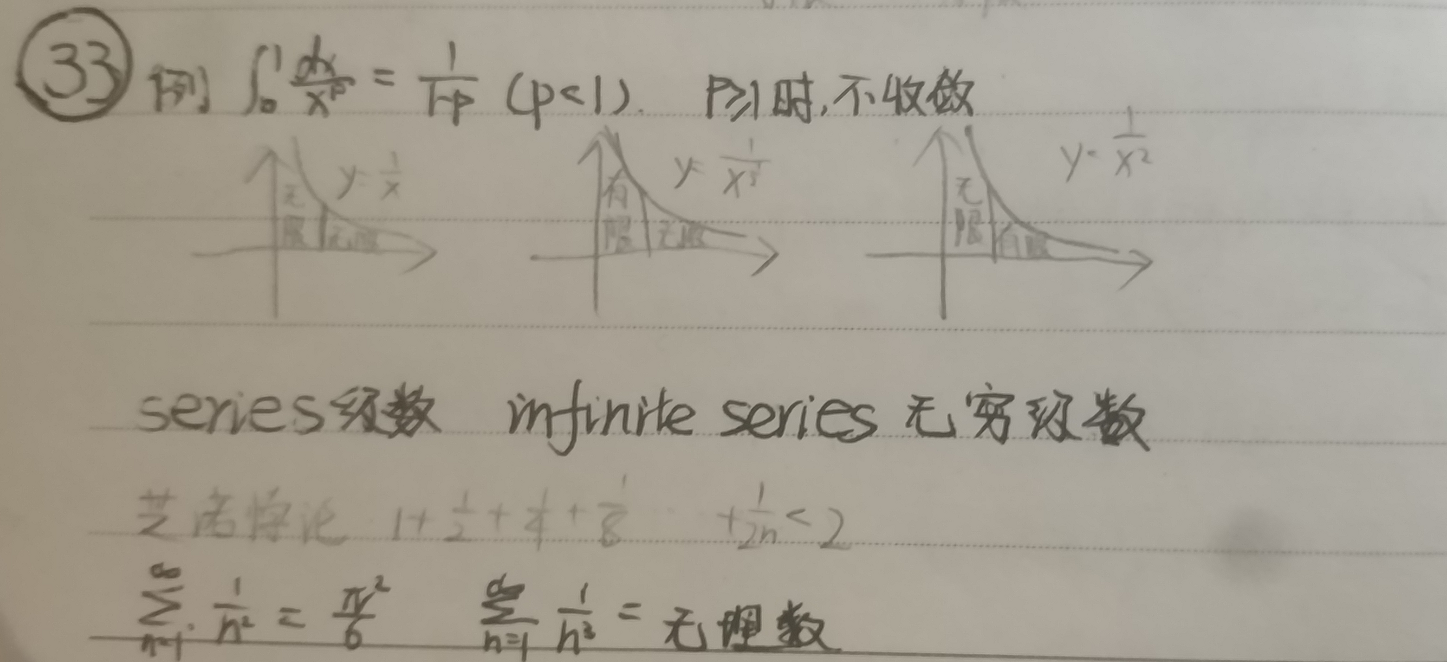
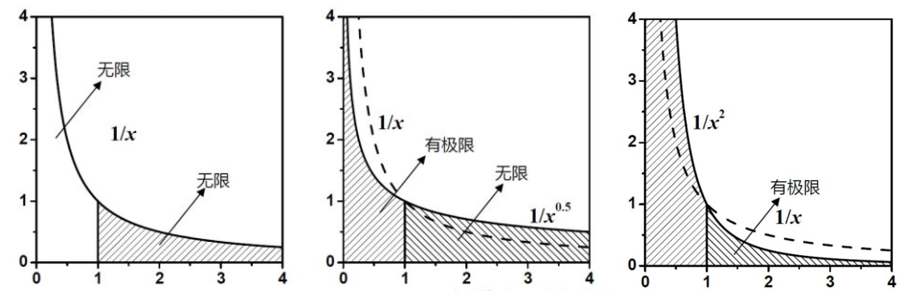
示例:讨论$\int_0^1\frac{dx}{x^p}$的收敛性
- $\int_0^1\frac{dx}{x^p}=\frac{x^{-p+1}}{-p-1}|_0^1=\frac{1}{1-p}(p<1)$
- 当$p\geq1$时,函数不收敛
总结3 反常积分示例中示例3的结果可得到以下结果:
2 无穷级数 infinite series
芝诺悖论:$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...++\frac{1}{2n}<2$
几何级数的通式:$1+a+a^2+a^3+...=\frac{1}{1-a}\ \ (|a|<1)$
级数求和与极限值:$S=\Sigma_{n=0}^{\infty}a_n=lim_{N\to \infty}S_N$
示例1:$\Sigma_{n=0}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$, 示例2:$\Sigma_{n=0}^{\infty}\frac{1}{n^3}=无理数$
3 极限比较 limits comparison
$$IF \ f(x)\sim g(x) \ \ \ THEN \ \ lim\frac{f(x)}{g(x)}\to1 \ \ as \ \ n\to \infty$$
示例1:$\Sigma\frac{1}{\sqrt{n^2+1}}\leftrightarrow \Sigma\frac{1}{\sqrt{n^2}}=\Sigma\frac{1}{n}$ 不收敛
示例2:$\Sigma\frac{1}{\sqrt{n^5-n^2}}\leftrightarrow \Sigma\frac{1}{\sqrt{n^5}}=\Sigma\frac{n^2}{n^5}$ 收敛
4 参考: