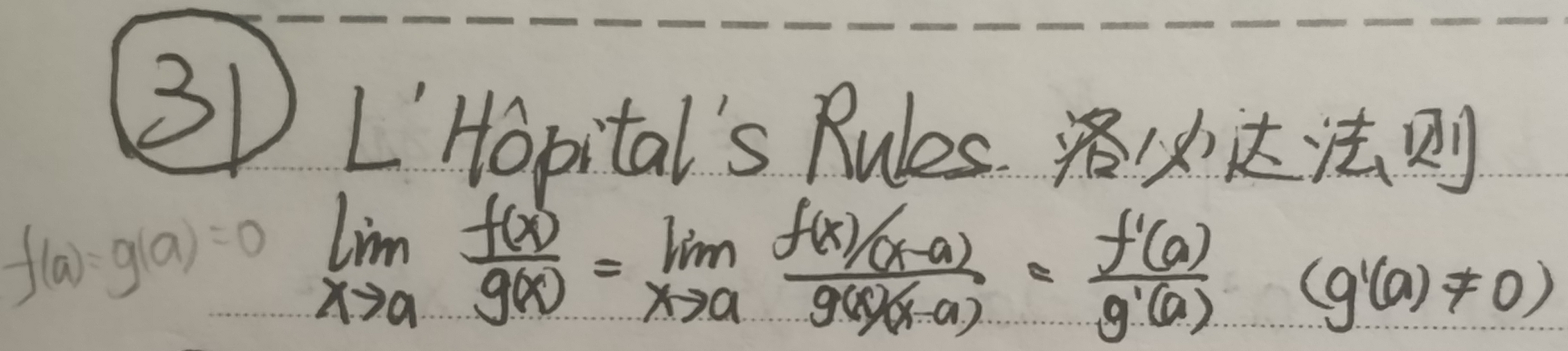1 洛必达法则
洛必达法则(L'Hopital's Rules):当$f(a)=g(a)=0$
$$lim_{x\to a}\frac{f(x)}{g(x)}=lim_{x\to a}\frac{f(x)/(x-a)}{g(x)/(x-a)}=\frac{f'(x)}{g'(x)}(g'(x)\neq0)$$
2 洛必达法则示例
$$lim_{x\to 0}\frac{sin5x}{sin2x}=lim_{x\to 0}\frac{5cos5x}{2cos2x}=\frac{5}{2}$$
$$lim_{x\to 0}\frac{cosx-1}{x^2}=lim_{x\to 0}\frac{-sinx}{2x}=\frac{-cosx}{2}=-\frac{1}{2}$$
洛必达法则最大的用处是处理$\frac{0}{0}$和$\frac{\infty}{\infty}$的情况
$$lim_{x\to 0^+}xlnx=lim_{x\to 0^+}\frac{lnx}{1/x}=lim_{x\to 0^+}(-x)=0$$
$$lim_{x\to 0}x^x=lim_{x\to 0}e^{xlnx}=lim_{x\to 0}e^0=1$$
3 参考