1 木板问题
将1号木板放置在桌面边缘,在木板不掉落的情况下不断探出;然后再叠加2号木板,追求总探出长度最大的情况,以此类推,判断最终总长度是否是有限的
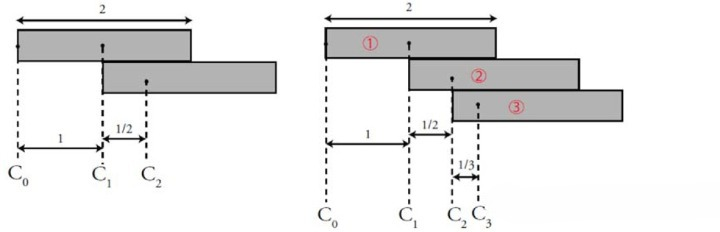
- 要保证积木不掉落,就需要保持整体的重心在桌面内
- 贪婪情况下(追求总长度最长),重心会保持在桌面边缘处
- 判断最终总长度是否有限,其实是判断$C_N$的极限是否收敛的问题
- 用$C$表示重心的水平方向值,则$C_N$表示叠加$N$个积木后的整体重心
- $C_{N+1}=\frac{NC_N+1\times(C_N+1)}{N+1}=C_N+\frac{1}{N+1}$
- 由此可得$C_N=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{N}$
- 由此可得$lnN<C_N<(lnN)+1$,其中$lnN$是黎曼下和,而$(lnN)+1$是黎曼上和
- 所以随着$N\to \infty$,$C_N \to \infty$,总长度是无限的
课堂冷知识
- 假设木板长度为2,桌子长为26,若希望探出长度达到24,则需令$lnN=24$,即$N=e^{24}$,假设每块木板厚$3cm$,最终高度为$3cm\times e^{24}\approx 8\times 10^8m$,相当于地月距离的两倍~
- 受限于$lnx$的缓慢增长,木块叠加至无限远仅存在于理论情况
- 忽略木板厚度,连接所有叠加木板的右下角构成的曲线是对数曲线
2 幂级数 power series
$$a_0+a_1x+...+a_nx^n=\Sigma_{n=0}^{\infty}a_nx^n$$
- 当$|x|<R$时,幂级数是收敛的,其中$R$表示收敛半径
- 当$|x|>R$时,幂级数是发散的,无意义的
示例(几何级数):$1+x+x^2+...=\frac{1}{1-x}$,在$x\geq 1$时无意义
3 泰勒公式 Taylor's formula
泰勒公式是用特殊系数的幂级数形式来表示函数的一种方法:
$$f(x)=\Sigma_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n$$
示例1:$e=e^x\ (x=0)=\Sigma_{n=0}^{\infty}\frac{1}{n!}0^n=1+1+\frac{1}{2!}+\frac{1}{3!}+...+\frac{1}{n!}$
示例2:$sinx=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...(R=\infty)$
示例3:$cosx=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+...(R=\infty)$
4 参考
