1 最值的应用
复习:分析函数极值点关键是找到驻点、边界点和不连续点
例:1根绳,截2段,分别围成正方形,求总面积最大值 $$S=(\frac{x}{4})^2+(\frac{1-x}{4})^2$$
- 其中$x$表示绳子第一截的长度
- $1-x$表示绳子第二截的长度
- $S$表示最后两个正方形的总面积
求解过程
- 令$S'=0$,可得$x=\frac{1}{2}$
- 此时$S(x=\frac{1}{2})=\frac{1}{32}$,是最小值
- 此函数的最大值为边界值,即$x=0^+or1^-$的时候最大
- 此时$S=\frac{1}{16}$,是总面积最大值
2 相关变率
例:警察在离公路30英尺的地方监测超速情况,他距离你50英尺远,并且发现你的车沿着雷达方向以每秒80英尺的速度逼近。求是否超速(限速$v=95ft/sec$)?
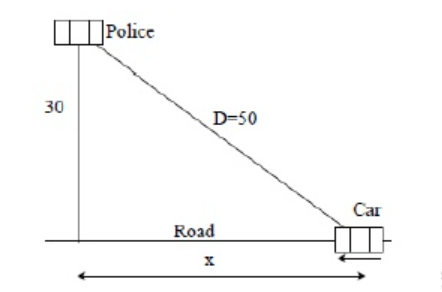
求解过程
- 由题意可知$x^2+30^2=D^2$且$\frac{dD}{dt}=80$
- 代入$D=50$解得$\frac{dx}{dt}=\frac{dx}{dD}\frac{dD}{dt}=100$
- $100>95$,超速了,赠白银手链一副
注:本题的求解过程来自下一节课,出于内容的完整性,移至此处
3 参考
