1 牛顿迭代法误差分析
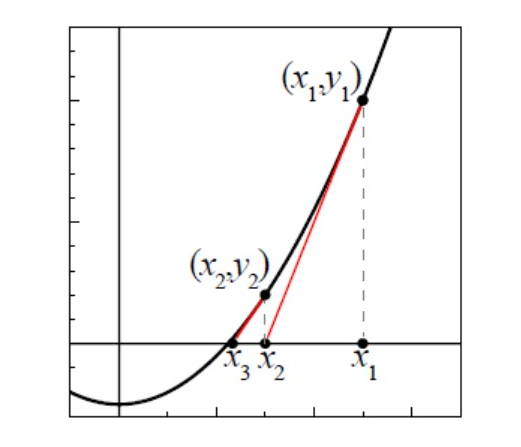
- 设真实解为$x$,真实解与第$n$次迭代后的近似解误差为$E_n=|x-x_n|$
- 则$E_1=|x-x_1|$,且$E_2=|x-x_2|=|x-x_1+\frac{f(x_1)}{f'(x_1)}|$
- 考虑到图示中$(x-x_1)<0$且$f'(x_1)>0$,所以$E_2$相比于$E_1$减小了$\frac{f(x_1)}{f'(x_1)}$
- 粗略来看,$E_2$误差减小量和$x_1$呈现线性关系,所以$E_2\approx E_1^2$
牛顿迭代法的条件限制
- $|f'(x)|$不能太小
- $|f''(x)|$不能太大(因为当$f''(x)=0$时,牛顿法可以得到准确解;而$f''(x)$越大,函数弯曲程度越大,误差也就越大)
- 初始值$x_1$不能离真实解$x$太远
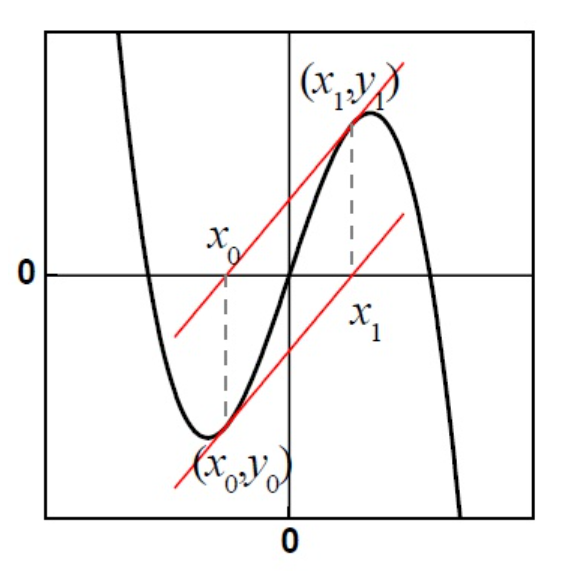
牛顿迭代法的两大陷阱
- $f'(x_n)=0$,此时切线水平,找不到下一个点$x_{n+1}$,算法宕机
- 迭代法出现死循环,比如$x_n\to x_{n+1}\to x_{n+2}$,而$x_n=x_{n+2}$
2 中值定理 MVT(mean value theorem)
$$\frac{f(b)-f(a)}{b-a}=f'(c)$$
- 其中$c$满足$a<c<b$
- 函数$f$在$(a,b)$上可微
- 函数$f$在$[a,b]$上连续
中值定理证明:(图解法)
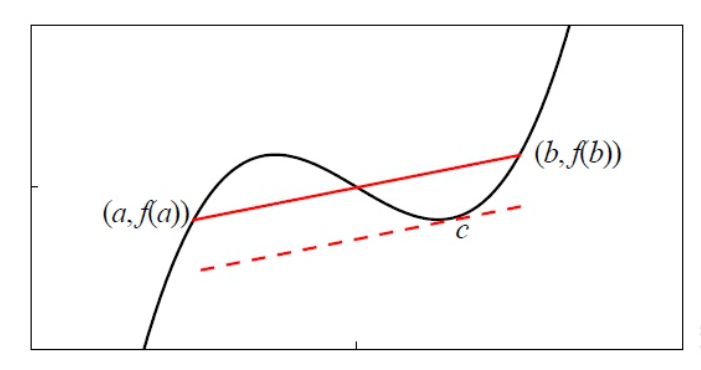
补充:符号中值定理的$c$的个数与$f''$有关,$c$的个数=拐点数+1
3 中值定理三大推论
- 若$f'>0$,则函数递增
- 若$f'<0$,则函数递减
- 若$f'=0$,则函数为常数
推论的证明:
- 令$a<b$,由中值定理可得 $f(b)=f(a)+f'(c)(b-a)$
- 易得,三大推论成立
4 中值定理VS线性近似
中值定理 $$f_{min}'\leq \frac{f(b)-f(a)}{b-a}=f'(c) \leq f_{max}'$$
- 是一种范围和存在性的确定
线性近似 $$f(x) \approx f(x_0)+f'(x_0)(x-x_0)$$
- 是一种极短区间内的近似
5 不等式 inequality
$$e^x>1+x+\frac{x^2}{2}+\frac{x^3}{3\times 2} +\frac{x^4}{4\times 3\times 2}...+\frac{x^n}{n!}$$
不等式证明
- 先证明$e^x>1+x$
- 令$f(x)=e^x-(1+x)$,并且可知$f(0)=0$
- 在$x>0$的前提下,$f'(x)=e^x-1>0$,所以$e^x>1+x$
- 再证明$e^x>1+x+\frac{x^2}{2}$
- 令$g(x)=e^x-(1+x+\frac{x^2}{2})$,并且可知$g(0)=0$
- 而$g'(x)=e^x-1-x>0$,所以$e^x>1+x+\frac{x^2}{2}$
- 重复以上过程,可实现证明
6 参考

