1 何为导数 derivative
- 几何解释 geometric interpretation
- 物理解释 physical interpretation
- 导数全方位的重要性 importance to all measurements
2 如何对已知的任意函数求导
- 思考:如何对$e^{xarctan(x)}$求导
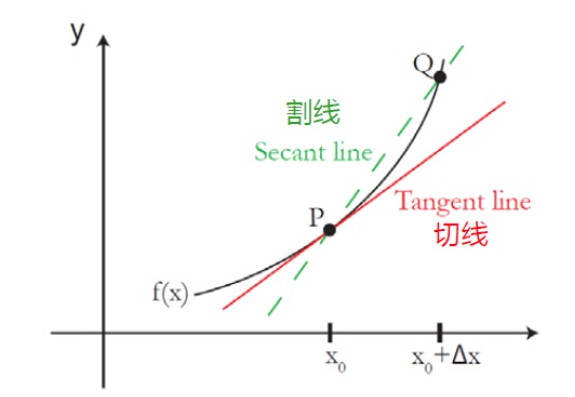
导数的几何解释
- 选择函数曲线上的点$P$,其坐标值为$(x_0,y_0)$
- $x_0$沿着x轴(x-axis)移动一段距离$\Delta x$,其对应的点为$Q$
- 定义割线(secant line)为过点$P$到点$Q$的直线
- 随着点$Q$趋近于点$P$,割线将逐渐趋近于点$P$的切线
- 导数的几何意义为切线的斜率,即两点极限逼近下割线的斜率
导数的定义 $${f}'(x)=\lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$
- 其中$\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$表示差商(difference quotient)
3 练习题
3.1 Example 1
题目:函数求导$f(x)=\frac{1}{x}$ $$\frac{\Delta f}{\Delta x}=\frac{\frac{1}{x_0+\Delta x}-\frac{1}{x_0}}{\Delta x}=\frac{1}{\Delta x}\left(\frac{-\Delta x}{(x_0+\Delta x)x_0} \right)$$ 取极限$\Delta x \to0$,可得 $$\lim_{\Delta x \to 0}\frac{\Delta f}{\Delta x}=\frac{-1}{x_0^2}$$
扩展:$f(x)=\frac{1}{x}$在任意点切线与x轴、y轴组成三角形面积恒为2
3.2 Example 2
题目:函数求导$f(x)=x^n$ $$\frac{\Delta f}{\Delta x}=\frac{(x_0+\Delta x)^n-x_0^n}{\Delta x}$$ 由二项式定理(the binomial theorem)可得 $$(x_0+\Delta x)^n=\Sigma_{k=0}^nC_{n}^{k}x_0^{n-k}\Delta x^k$$ 取极限$\Delta x \to0$,可得 $$\lim_{\Delta x \to 0}\frac{\Delta f}{\Delta x}=\frac{C_{n}^{1}x_0^{n-1}\Delta x}{\Delta x}=nx_0^{n-1}$$
4 参考