1 平面方程
方程$ax+by+cz=d$定义了一个平面,此方程的矩阵形式如下: $$\left[ \begin{matrix} a \\ b \\ c \\ \end{matrix} \right] \cdot \left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right] =d$$ 上面的式子也可以整理如下: $$\left[ \begin{matrix} a \\ b \\ c \\ \end{matrix} \right] \cdot \left[ \begin{matrix} x-x_0 \\ y-y_0 \\ z-z_0 \\ \end{matrix} \right] =a(x-x_0)+b(y-y_0)+c(z-z_0)=0$$ 上式即平面的一般方程,易得向量$<a,b,c>$与向量$<x-x_0,y-y_0,z-z_0>$垂直
对于此平面方程来说,向量$<a,b,c>$表示法向量,数值$d$包含了平面的平移信息(平移距离),向量$<x,y,z>$的所有可能构成了平面
2 平面方程的类型:
假设原点设为$O$,并且点$P=[x,y,z]$始终在平面上,$\vec{N}$表示平面的法向量
情况1:平面过原点
- 根据法向量特性,易得$\vec{OP}\cdot \vec{N}=0$
- 联系上一节,相当于$d=0$,即平面不存在平移信息
- 此时可称该平面方程是齐次的
情况1:平面不过原点,但过点$P_0$
- 根据法向量特性,易得$\vec{P_0P}\cdot \vec{N}=0$
- 联系上一节,相当于$d\neq0$,即平面存在平移信息
- 此时可称该平面方程是非齐次的
3 线性方程组的几何理解
以$3\times 3$线性方程组为例,从几何角度思考方程组解的所有可能。$3\times 3$线性方程组可以拆解为三个平面方程,所以方程组的每一种解对应着三个平面产生交会的点
- 三个平面相交于一点,此时方程组存在唯一解
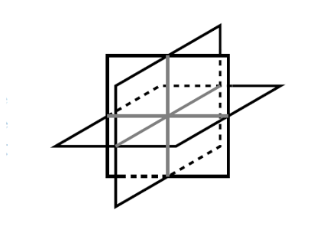
- 三个平面相交于线或面(重叠),此时方程组存在无数解
- 三个平面相交没有共同交点,此时方程组不存在解
4 参考