贝叶斯优化是一种通用的黑盒优化算法，不需要计算梯度便可快速解决最优化问题，贝叶斯优化适合处理目标函数计算成本高或求导困难的情况。贝叶斯优化最常用的场景是超参搜索（尤其是神经网络类算法，计算成本高，超参数还多）
1 贝叶斯优化与代理模型
贝叶斯优化(Bayesian Optimization，BO)
目的是要找到一组最优的超参组合x，能使评价/目标函数f(x)达到全局最优
由于评价/目标函数f(x)计算成本通常较高，所以贝叶斯优化采用代理模型(surrogate model)策略
代理模型可以被看作是一个相对简单模型，用来拟合原本复杂且不好理解的模型
代理模型最常见的构造方法就是高斯过程(gasussian processes, GP)，此时的贝叶斯优化也被称为GP-BO
比如说，给定4个采样点（输入/参数组合，输出/评价值）后高斯过程能够推断并给出如下图所示的模型：
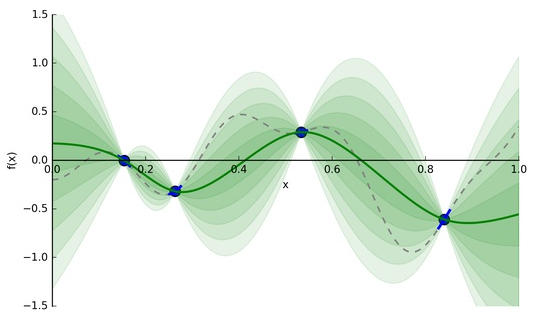
上图中，绿色实线标识GP构建的用于近似替代f(x)的代理模型，而绿色条带是代理模型的置信区间
给定一组新的超参超参并带入代理模型后，代理模型能在计算开销相对较小的情况下对超参数进行评估
除了计算成本高之外，目标函数还可能因为非凸、不可微、噪声大等问题，此时也可以考虑使用代理模型，除此之外，当目标函数的可行集比较简单或存在边界约束时（比如限制超参数必须是整数，且处于1~10之间），也很适合使用代理模型
除了高斯过程外，代理模型也可以用其他的常见建模方式取代，比如线性模型、贝塔-伯努利(Beta-Bernoulli)模型、广义线性(generalized linear)模型、随机森林、神经网络等待。只要在维持较低的计算成本的同时能近似替代原始目标函数即可
2 贝叶斯优化的迭代决策
贝叶斯优化是一个迭代式的决策过程
- 通过实际采样和高斯过程，可以构建出代理模型用来快速估计不同超参组合的评价值
- 但是完整的贝叶斯优化过程还需要考虑：如何选择下一组超参组合进行评估？
- 决策过程既要考虑到已知的优质超参组合的开发（Exploitation），还要兼顾未知区域的探索（Exploration）
- 一个出色的贝叶斯优化过程需要构建一种探索和开发的平衡(exploration-exploitation trade-off)
贝叶斯优化有很多种采集策略来寻找下一组超参组合的选择（也可以随机选择，但是效率低）
2.1 基于提升的策略
基于提升的策略追求目标函数的最大化，并通过构建采集函数实现探索和开发的平衡
常见的两种提升策略是PI最大化采集策略和EI最大化采集策略
2.1.1 PI采集策略
PI（probability of improvement）采集策略高斯回归GP为例，第t次迭代构建的代理模型可表示如下： $$f_t(x)\sim N(u_t(x),\sigma_t^2(x))$$
- 其中$u(t)$为均值函数，$\sigma_t(x)$为标准差函数
- 给定$x$后，$f(x)$的输出结果是具备置信区间的随机向量
对于第t+1次迭代，PI采集函数（Acquisition Functions）可定义如下： $$PI_t(x)=P(f_t(x)\geq (f_t^+ + \epsilon))=\Phi(\frac{u_t(x)-f_t^+-\epsilon}{\sigma_t(x)})$$
- $f^+_{t}=max_{t'=1,...,t}f(x_{t})$表示前$t$次迭代中的最大值
- 上式中$P(f_t(x)\geq (f_t^+ + \epsilon))$为通式，最右侧是代入GP代理模型后的结果
- $\Phi$表示满足标准正态分布的累积分布函数(cumulative distribution function CDF)
- $\epsilon$为平衡参数，用来平衡开发（Exploitation）和探索（Exploration）
PI策略通过PI提升最大化来选择新一轮的超参组合： $$x_{t+1}=argmax_x(PI_t(x))=argmax_x(\Phi(\frac{u_t(x)-f_t^+-\epsilon}{\sigma_t(x)}))$$
- PI策略寻找目标值比$f^+_t+\epsilon$更大的候选点，并选择其中最大概率
- 当$\epsilon$较大时，PI策略更偏向于全局搜索，探索（Exploration）标准差较大的区域
- 当$\epsilon$较小时，PI策略更偏向于局部搜索，开发（Exploitation）均值较大的区域
补充说明1：本文假设目标函数越大越好，在有些问题或场景中，可能需要采用诸如损失函数或成本函数作为最优化目标。此时目标函数应该是越小越好的，这两种情况只是一个正负号的差别，其本质是一致的
补充说明2：$f_t(x)$是真实目标函数值的近似，在每轮迭代并获取到新的$x$后，还会进行一次成本较高的真实目标函数值的计算，用来指导$f_t(x)$在下一轮迭代过程中的更新，使其预测结果更接近真实值
2.1.2 EI采集策略
PI策略选择提升概率最大的候选点, 这一策略值考虑了提升的概率而没有考虑提升量的大小
EI（expected improvement）策略针对这一问题进行了改进，EI采集函数（Acquisition Functions）定义如下： $$EI_t(x)=E[max(f_t(x)-f^+,0)]$$
以下推导过程略有些复杂，不感兴趣的读者可直接跳过查看最终的公式及其解读
为方便推导和理解，定义服从标准正态分布的随机变量$z\sim N(0,1)$，其对应的概率密度函数为$\phi(z)$，累积分布函数为$\Phi(z)$
由高斯过程得到的代理模型可表示为$f_t(x)\sim N(u_t(x),\sigma_t^2(x))$，所以由$f_t(x)=u_t(x)+z\sigma_t(x)$可得： $$z=\frac{f_t(x)-u_t(x)}{\sigma_t(x)}, \ \ z^+=\frac{f^+-u_t(x)}{\sigma_t(x)}$$ 经此标准化变换后，EI采集函数转化为： $$EI_t(x)=\int_{-\infty}^{z^+}(u_t(x)+z\sigma_t(x)-f^+)\phi(z) dz+\int_{z^+ }^{+\infty}(u_t(x)+z\sigma_t(x)-f^+)\phi(z) dz$$ 由EI采集函数定义中可知$f_t(x)<f^+$时，也就是$z<z^+$时，EI采集函数结果恒为0，所以上式左侧可直接忽略
之后对左侧剩余部分进行拆分，拆成两个积分项并进行化简： $$EI_t(x)=\int_{z^+ }^{+\infty}(u_t(x)+z\sigma_t(x)-f^+)\phi(z) dz=(u_t(x)-f^+)\int_{z^+ }^{+\infty}\phi (z)dz+\int_{z^+ }^{+\infty}z\sigma_t(x)\phi(z) dz$$ 对于左侧积分项，可以直接利用概率密度函数为$\phi(z)$和累积分布函数$\Phi(z)$的关系，进行化简： $$(u_t(x)-f^+)\int_{z^+ }^{+\infty}\phi(z) dz=(u_t(x)-f^+)(1-\Phi(z^+))=(u_t(x)-f^+)\Phi(-z^+)$$ 对于右侧积分项，需要带入$\phi$的原始形式（标准正态分布的概率密度函数）$\phi(z)=\frac{exp(-z^2/2)}{\sqrt{2\pi}}$并进行化简： $$\int_{z^+ }^{+\infty}z\sigma_t(x)\phi(z) dz=\int_{z^+ }^{+\infty}z\sigma_t(x)\frac{exp(-z^2/2)}{\sqrt{2\pi}} dz=\left[\sigma_t(x) \frac{exp(-z^2/2)}{\sqrt{2\pi}} \right]_{z^+}^{+\infty}=\sigma_t(x) \phi(z)$$ 汇总左侧积分项结果和右侧积分项结果后，再将$z$替换为$f_t(x)$： $$EI_t(x)=(u_t(x)-f^+)\Phi(-z^+)+\sigma_t(x) \phi(z)=(u_t(x)-f^+)\Phi(\frac{f^+-u_t(x)}{\sigma_t(x)})+\sigma_t(x) \phi(\frac{f_t(x)-u_t(x)}{\sigma_t(x)})$$
最终的EI采集函数如下所示： $$\begin{equation} EI_t(x) = \left\{ \begin{array}{rl} (u_t(x)-f^+)\Phi(\frac{f^+-u_t(x)}{\sigma_t(x)})+\sigma_t(x) \phi(\frac{f_t(x)-u_t(x)}{\sigma_t(x)}) & \mbox{if } x_t(x) > 0, \\ 0 & \mbox{if } \sigma_t(x) = 0, \\ \end{array} \right. \end{equation}$$
- 对于$\sigma_t(x) = 0$的情况，对应训练集中的样本点，也可以理解为已确定、已探明的区域
- 策略左半部分是在考虑f(x)历史最大值的情况下追求f(x)更高的情况，是对已开发组合的考虑
- 策略右半部分是在最追求方差更高的情况，是对未知区域的探索
- 将$f^+$替换为$f^+ +\epsilon$可以引入平衡参数，其效果与PI策略是一样的
和PI策略类似，EI策略通过EI提升最大化来选择新一轮的超参组合： $$x_{t+1}=argmax_x(EI_t(x))$$
补充说明：PI策略倾向于寻找最大概率的超参组合，而EI策略倾向于寻找最大提升度的超参组合；二者存在一定的互补，在实际场景中可以考虑两种策略融合使用，充分发挥出各自的优势
2.2 置信边界的策略
2.2.1 UCB采集策略
沿用高斯过程回归GPR作为代理模型，在求解目标函数最大值时, UCB策略的采集函数为 $$x_{t+1} = argmax_xUCB=argmax_x(\mu_t(x)+\sqrt{\beta_t}\sigma_t(x))$$
- GP-UCB很简单的一种采集策略，以随机变量的置信上界最大化为原则选择下一轮的超参组合
- UCB策略倾向于选择均值高且标准差大的区域，其中调节参数$\beta$可以用来平衡期望和方差的权重
- 当目标函数越小越好时，可考虑使用置信下界策略GP-LCB（其实上式就是加一个符号）
UCB这一概念其实是来自强化学习领域中的多臂老虎机（multi-armed bandit或MAB）问题，在之前研究蒙特卡洛树搜索算法和AlphaGo Zero原理的文章中都有涉及到过
2.3 基于信息的策略
2.3.1 汤普森抽样
沿用高斯过程回归GPR作为代理模型，汤普森抽样(Thompson sampling, 简称TS)步骤其实很简单
- 首先对高斯过程结果进行一次随机采样，得到一个高斯分布$\hat{f}_t$
- 之后基于高斯分布$\hat{f_t}$，多次采样超参组合并选择最佳的一组：
$$x_{t+1}=argmax_{x\in X}\hat{f_t}$$
和UCB一样，汤普森抽样也是从强化学习领域中的多臂老虎机（multi-armed bandit或MAB）问题中移植过来的方法，其核心思路和UCB采集存在相似性，只不过汤普森抽样使用抽样的方法找到一个合理的上界，而UCB是直接计算给出上界
2.3.2 熵搜索策略
熵搜索策略（entropy search, 简称ES）的主要思想是最大程度减少全局最优解$x^{\ast}$的不确定性
熵搜索策略可表示如下的形式： $$x_{t+1}=agmax_{x\in X} H(P(x^{\ast}|D_{t}))-E_{y|D_t,x}[H(P(x^{\ast}|D_t\cup (x,y)))]$$
- 其中全局最优解$x^{\ast}$在超参搜索任务中就是指最优的超参组合
- $H(p(x))=\int p(x)log(p(x))dx$表示$p(x)$的微分熵（描述了$p(x)$的一种不确定性）
- $y|D_t,x=f_t(x)+\epsilon\sim N(\mu_t(x),\sigma_t^2(x)+\sigma^2)$，其中$\epsilon$为服从标准正态分布的噪声
- 微分熵和$P(x^{\ast}|D_t)$都是很好计算，一般需要通过采样的方式进行近似估计
熵预测搜索（predictive entropy search, 简称PES）策略在ES策略的基础上进行了优化：该方法利用$x^{\ast}$和$y$之间互信息的对称性对公式进行了简化，简化后的公式如下： $$x_{t+1}=agmax_{x\in X} H(P(y|D_{t}))-E_{x^{\ast}|D_t,x}[H(P(y|D_t,x,x^{\ast}))]$$
- PES和ES的结果是完全等价的，但近似计算简单了很多，是一种较为先进的熵搜索策略
2.4 其他策略概述
（血条已空，有缘再看）
- Max-Value Entropy Search：熵搜索算法，在PES的基础上，把$x^{\ast}$分布换成的$y^{\ast}$分布
- knowledge gradient（KG）：在EI策略上进行改进，追求两次代理模型的最优解的差异最大
- GP-Hedge：使用对冲策略组合多种采集函数（如PI、EI、UCB等），最终结果的鲁棒性更强
- entropy search portfolio（ESP）：熵搜索方法，倾向于选择可为全局最优解提供最多信息的候选点
2.5 贝叶斯优化总结
贝叶斯优化有两个核心过程，构建代理模型与进行迭代决策
- 其中构建代理模型常通过高斯过程回归等方面，模拟目标函数的先验分布，实现低成本的目标值计算
- 而迭代决策过程则主要借助采集函数(Acquisition Function,AC)，寻找下一组合理的样本并计算真实的目标值
- 代理模型为迭代过程的样本合理性估计提供了低廉的计算成本
- 而采集函数指导下的新样本则会反过来指导代理模型的优化迭代
在TPE论文中，作者围绕贝叶斯优化提出了SMBO框架对以上过程进行了总结
常见的不同采集策略的效果对比：
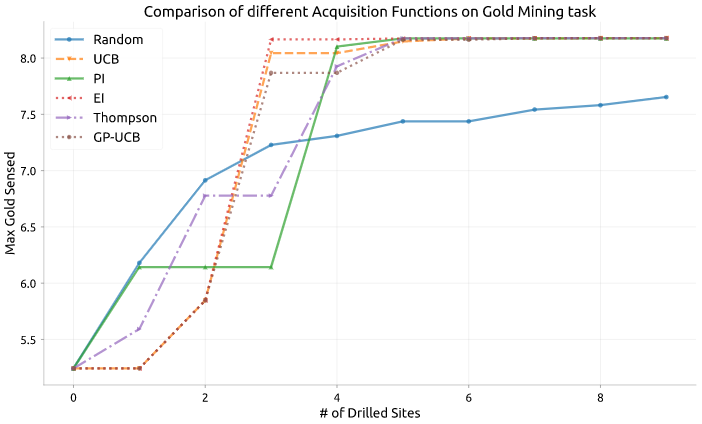图源：Exploring Bayesian Optimization
参考
贝叶斯优化方法和应用综述
贝叶斯优化/Bayesian Optimization
Acquisition functions in Bayesian Optimization